Il nostro amico Francesco ha dato una risposta corretta al quiz, utilizzando un sistema e risolvendolo nelle sue variabili. Allo stesso risultato si può anche arrivare con il solo ragionamento, utilizzando soltanto somme, differenze e divisioni...

Il primo passo non differisce da quanto descritto da Francesco.

Consideriamo soltanto il ramo sinistro della bilancia. Il suo peso totale deve essere 48 kg. Dividendo questa quantità nei successivi rami, otteniamo immediatamente la Fig. 1.

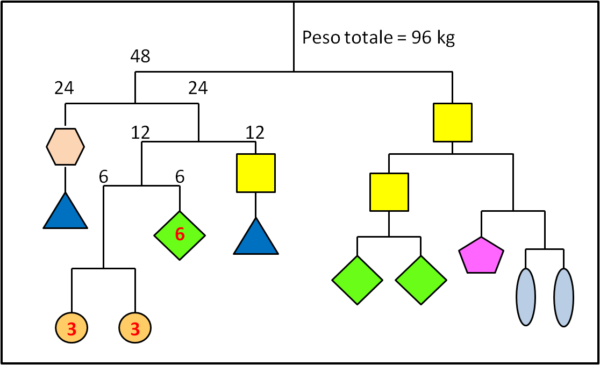
Si conclude banalmente che l'esagono deve pesare 6 Kg e che lo stesso peso deve essere ottenuto dai due cerchi, ossia:

rombo = 6 Kg

cerchio = 3 Kg

Passiamo ora al ramo di destra. Per potere scendere verso il basso è necessario sapere quanto vale il peso del quadrato. Sicuramente il suo peso ha dei vincoli evidenziati da quanto si ottiene dai rami di sinistra. In particolare, vediamo che la somma del peso del quadrato e del triangolo non può superare 11 Kg, dato che se fosse 12 il peso del triangolo sarebbe 0, ossia impossibile. Ne segue che il peso del quadrato può valere solo i numeri da 1 a 11. Non tutti però sono accettabili, dato che 3 e 6 sono già stati usati. Rimangono perciò le seguenti possibilità:

quadrato = 1

quadrato = 2

quadrato = 4

quadrato = 5

quadrato = 7

quadrato = 8

quadrato = 9

quadrato = 10

Oh... mamma mia! Come trovare il peso giusto? Si può andare per tentativi, ma prima possiamo ancora limitare le possibilità.

Infatti, per ottenere il peso del ramo di sinistra basta fare 48 meno il peso del quadrato. Ma se il peso del quadrato fosse un numero dispari lo sarebbe anche il peso del ramo sotto di lui (pari meno dispari uguale dispari). A questo punto questo numero dispari dovrebbe essere diviso per due, dando come risultato un numero frazionario. E questa è una situazione impossibile, dato che tutte le figure devono avere peso intero.  Sono, perciò, da escludere tutte le possibilità dispari per il peso del quadrato.

Rimangono, perciò, solo 4 possibilità:

quadrato = 2

quadrato = 4

quadrato = 8

quadrato = 10

E' veramente immediato potere escludere i valori impossibili: basta infatti togliere a 48 il peso del quadrato e controllare se il ramo destro dopo il quadrato ha un valore plausibile.

Se valesse 2 o 10 avremmo che 48 - 2 = 44, per cui 46/2 = 23. Impossibile perché dispari. Idem per 10: 48 - 10 = 38, da cui 38/2 = 19 dispari!

Ci rimangono solo due possibili valori :  4 e 8

Proviamo con 4, ossia P = (48 -4)/2 = 22

6 + 6 + 4 = 16      NO, da scartare perché 12 NON è uguale a 22.

Non ci rimane che il numero 8 (deve essere quello giusto!)

P = (48 -8)/2 = 20

6 + 6 + 8 =20           PERFETTO!

Il peso del quadrato non può essere che 8. Ricapitolando:

cerchio = 3

rombo = 6

quadrato = 8

Rimaniamo nel ramo di destra della bilancia. Possiamo scrivere i pesi dei rami discendenti dato che ormai sappiamo quanto vale il peso del quadrato. Riportiamo la situazione in Fig. 2.

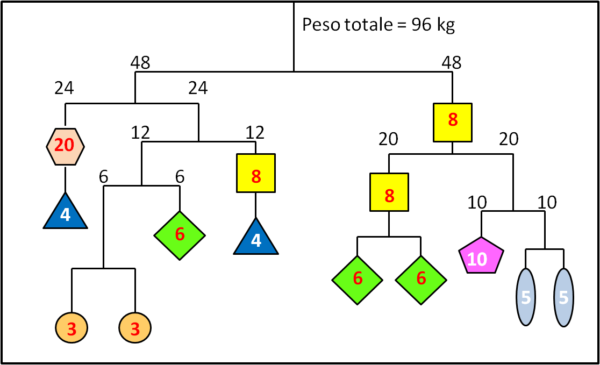
I rami discendenti hanno valori 20 e poi 10. Per cui...

pentagono = 10

ellisse = 5

Possiamo concludere il tutto spostandoci nel ramo principale di sinistra.

Il ramo più a destra è formato da un quadrato e un triangolo e ha peso 12. Essendo il quadrato di peso 8, ne segue che il triangolo ha peso 4.

Infine, il ramo più a sinistra, ha peso 24, di cui 4 sono dovuti al triangolo, per cui:

esagono = 20

In conclusione:

rombo = 6 Kg

cerchio = 3 Kg

quadrato = 8 Kg

pentagono = 10 Kg

ellisse = 5 Kg

triangolo = 4 Kg

esagono = 20 Kg

Senza ombra di dubbio, la versione "matematica" di Francesco è più elegante...