Categorie: Fisica classica Matematica
Tags: due giri di pista quiz velocità media
Scritto da: Vincenzo Zappalà
Commenti:16
(QI) Due giri di pista ... ***
Devo effettuare due giri di pista. Il primo giro lo devo compiere a velocità costante, ma posso effettuarlo anche in modo estremamente lento. Nel secondo invece devo andare molto più veloce, dato che voglio che la velocità media finale sia pari a due volte la velocità del mio primo giro. Ipotizziamo che allo scadere del primo giro riesca a raggiungere istantaneamente una nuova velocità costante. Mi chiedo:
"A che velocità devo effettuare il secondo giro?"
Sembra tutto molto semplice, ma lo è davvero... ?
P.S.: mi aspetto una discussione "accesa", malgrado le ferie.
QUI la soluzione






16 commenti
(v+v') / 2 = 2v
v+v' = 4v
v' = 3v
Che ingenuo che sono!
matematicamente "sembrerebbe" corretto, ma ...
Caro Enzo, tentar non nuoce, ma con sto caldo si cuoce.
Io proverei così.
La velocità media del secondo giro è uguale a:
Vm= (V2- V1)/2
dove V2 è la velocità finale e V1 quella all'inizio del secondo giro.
Dato che il primo giro l'ho fatto a velocità costante, quella dovrebbe coincidere con V1 ossia alla fine del primo giro che è l'inizio del secondo prima di accelerare.
Quindi:
Vm=2V1
(V2-V1)/2=2V1
V2/2 - V1/2 = 2V1
V2/2 = 2V1 + V1/2
V2/2= (4V1 + V1)/2
V2/2 = 5V1/2
V2 = 10V1/2
V2 = 5V1
Se il ragionamento è corretto la velocità finale al secondo giro dovrebbe essere pari a 5 volte quella del primo giro... oh no?
Vabbè diciamo che fa caldo, manco il calcolo della velocità media è corretto...
mi sa che c'è un problema spazio temporale
se raddoppio lo spazio da percorrerre (2 giri) ma devo tenere il tempo usato per percorrere la prima metà, a qualsiasi velocità finita faccia la seconda metà non potrò mai avere una velocità media maggiore o uguale a due volte la velocità del primo giro. Se facessi il secondo giro a velocità infinita (tempo zero) la velocità media sarebbe il doppio della velocità media del primo giro visto che ha fatto il doppio dispazio nello stesso tempo.
Ernesto
cari amici,
preferisco non dire niente, dato che vorrei un numero maggiore di risposte "non condizionate" prima di dare la soluzione e, magari, aprire un dibattito...
Mah...
dopo aver calcolato la velocità media come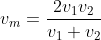 non riesco a concludere seriamente che
non riesco a concludere seriamente che 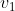 sia zero...
sia zero...
Risposta sintetica
∞
Caro Enzo, ora che ha fatto un temporalone, provo a riformulare la risposta.
Parto dalla velocità media.
Dato che ci son due velocità, V1 al primo giro e V2 al secondo:
Vm= (V1+V2)/2
Questa deve essere il doppio di V1:
(V1+V2)/2= 2 V1
V1+V2= 4 V1
V2= 4V1 - V1
V2= 3 V1.
Però, però...
Provo a calcolare la velocità media come rapporto tra spazio e tempo percorso.
Vm= 2S/(t1+t2)
Dove S è il percorso di 1 giro, ma in questo caso ne ho fatti 2, t1 il tempo necessario per percorrere il primo giri, t2 il tempo necessario per percorrere il secondo giro.
Ovviamente V1= S/t1
Quindi:
Vm= 2 V1
2S/(t1+t2)= 2S/t1
1/(t1+t2) = 1/ t1
t1= t1+t2
Ovviamente questa equazione é valida solo se t2=0
Se il tempo impiegato per percorrere il secondo giro è zero, allora la velocità V2 è infinita:
V2= S/t2 = n/0= infinito.
Se applico tale velocità V2 al primo risultato della velocità media, ossia:
V2= 3 V1
Se V2 è infinita, lo è anche V1
Forse il nostro Enzo ci sta giocando un simpatico scherzetto:
il quiz parla di velocità costante per giro e non su tratto rettilineo, per cui se il percorso è curvo, anche se la velocità angolare è costante, il vettore velocità tangenziale (quella tenuta dal corridore), cambia di direzione punto per punto sulla curva, per cui non è costante nella componente direzione...
No, caro Andy... non volevo arrivare a questa possibilità... Invece di una pista, possiamo anche parlare di due tratti rettilinei consecutivi di pari lunghezza.
Però, però, la tua idea potrebbe servire per complicare il quiz
Buonasera a tutti, è un po' di tempo che non passo su questo meraviglioso sito, ma purtroppo gli impegni vari e la pandemia mi ci hanno allontanato.
Il quiz è veramente bello, e mi cimento anche io.
Rammentandomi che la velocità media tenuta lungo un percorso non è la media delle velocità tenute sui singoli tratti, chiamiamo v1 la velocità media del primo giro, v2 quella del secondo
v1=S1/t1 (dove S1 è la lunghezza del primo giro e t1 il tempo impiegato a percorrerlo)
v2=S2/t2 (dove S2 è la lunghezza del secondo giro e t2 il tempo impiegato a percorrerlo)
Ma S1=S2 (si spera)
La velocità media sui due giri è:
V=(S1+S2)/(t1+t2)=2S/(t1+t2)
Se vogliamo che V sia il doppio di v1, allora:
V=2v1
2S/(t1+t2)=2S/t1
quindi, dividendo entrambe le parti per 2S (con S diverso da zero)
1/(t1+t2)=1/t1
pertanto, t2=0 ed il secondo giro lo devo percorrere istantaneamente.
Però vedo una seconda possibilità:
Se t1 fosse lunghissimo, tendente ad infinito (in altre parole vado molto lentamente, o sto quasi fermo, cioè con v1 tendente a zero), la v2 può essere qualsiasi, e la velocità media totale sarebbe esattamente il doppio della velocità del primo giro (ma anche il triplo o quello che vogliamo).
Infatti:
2v1=2x0=0
V=2S/(t1+t2)=limite (per t1 tendente all'infinito) 2S/(t1+t2)=0
Quindi V=2v1
Concludendo:
Se v1 diversa da zero, allora il secondo giro deve essere percorso istantaneamente (con tutti i problemi relativistici che questo comporta)
Se v1 è zero, v2 può essere qualsiasi (con tutti i problemi semantici e logici che comporta l'affermazione "compio il primo giro stando fermo")
Ciao e a presto
Opss, vedo che c'è un altro Francesco. Chiamatemi pure Cesco
caro Cesco,
se la v1 fosse uguale a zero non compierebbe mai il primo giro... Comunque, siete proprio bravi!
...e infatti il primo Francesco (io...) arrivava solo a dire: "non riesco a concludere seriamente che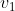 sia zero...".
sia zero...".
Che razza di quesito: ci sarà poi una risposta univoca? (magari senza tirare in ballo la relatività speciale ;-) )
v1 = s/t1
v2 = s/t2
vf = 2s/(t1 + t2) = 2v1 = 2s/t1 per ipotesi
Si ottiene quindi (semplificando s): 1/(t1 + t2) = 1/t1
da cui facendo il reciproco: t1 + t2= t1
ovvero t2 = 0
Impossibile! O, almeno, poco realistico
Legenda: inutile, è sufficiente un po’ di intuito