Categorie: Matematica Riflessioni
Tags: due pezzi puzzle quiz
Scritto da: Vincenzo Zappalà
Commenti:16
(Q) Il puzzle più difficile del mondo *
Probabilmente quello che vi propongo non è il puzzle più difficile in assoluto, ma lo è sicuramente se teniamo in conto il numero di "pezzi" che lo compongono: due soltanto.
Essi sono un trapezio rettangolo e un quadrato.
Il puzzle richiede di unire le due figure su di un piano (senza accavallarle) in modo tale che la figura finale sia divisibile in due parti perfettamente uguali (perfettamente sovrapponibili). Non basta avere aree uguali. La linea divisoria può essere qualsiasi.
Di seguito riporto le due figure di partenza in modo che possiate anche trasferirle su un cartoncino e ritagliarle.
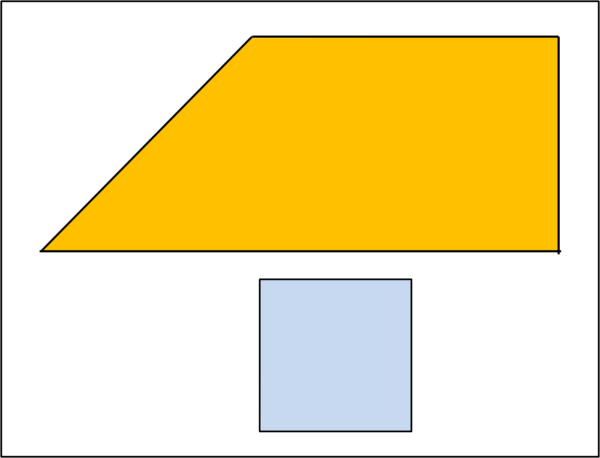
Il problema può essere affrontato anche sotto un ... ombrellone ed è risolvibile da chiunque: bastano fantasia e concentrazione.
I più esperti in geometria, però, aspettino qualche giorno...
N.B.: il quiz o puzzle che dir si voglia ha un solo asterisco perché abbisogna di una conoscenza veramente banale della geometria. Tuttavia, la sua soluzione può essere abbastanza ostica.
QUI un aiutino
QUI la soluzione






16 commenti
Proviamo da sotto l'ombrellone...
Sulla base maggiore del trapezio ricavo, partendo da uno dei vertici, il segmento differenza delle 2 basi e di quest'ultimo trovo il punto mediano. Unendo quest'ultimo con il vertice opposto del trapezio ottengo due figure di area uguale (un triangolo e un trapezio rispettivamente con base e somma delle basi uguali). Ci sono due possibili divisioni, una per vertice della base maggiore.
Unisco quadrato e trapezio originari facendo coincidere il punto mediano del quadrato con il nuovo punto trovato sulla base maggiore del trapezio e con una linea spezzata che taglia a metà il quadrato e prosegue fino al vertice opposto del trapezio, separo due poligoni con area uguale.
Scegliendo tra le due possibili divisioni quella che interseca la base con angolo da 45° a 135° e facendo passare la linea di divisione per il centro del quadrato accostato, riesco a dividere la nuova figura in due parti uguali con linea continua.
Chiedo scusa, caro Dario, ma non riesco a seguire il tuo procedimento...L'ideale sarebbe fare una figura. Potresti farla anche a mano e poi spedirla a Daniela.
Non capisco, infatti cosa intendi con:
"Ci sono due possibili divisioni, una per vertice della base maggiore"
Inoltre, anche questa costruzione mi risulta difficile da comprendere:
"quella che interseca la base con angolo da 45° a 135° e facendo passare la linea di divisione per il centro del quadrato accostato"
Ecco la figura di Dario:
Mi dispiace Dario, ma la soluzione non è valida...
Nel caso in alto abbiamo due aree uguali, ma due figure ben diverse tra loro.
Nel caso in basso, dopo il taglio, ottieni tre pezzi...
Ricorda i due pezzi finali devono essere perfettamente sovrapponibili!
Dico chiaramente: "in due parti perfettamente uguali", NON di area uguale.
Ho specificato l'uguaglianza ancor meglio nel testo...
Che sia veramente il più difficile al mondo???
Via libera a TUTTI !!!!
Caro Enzo,
attenendomi scrupolosamente al testo del quiz che richiede: "la figura finale sia divisibile in due parti perfettamente uguali (perfettamente sovrapponibili). Non basta avere aree uguali. La linea divisoria può essere qualsiasi", utilizzando solo due "pezzi".
Allora ho diviso il quadrato secondo una sua diagonale, ho ruotato mezzo quadrato sull'asse della diagonale e la mezza parte sovrapposta l'ho ruotato secondo l'asse passante per il lato del quadrato stesso;
ho poi accostato la diagonale del quadrato all'altezza del trapezio e le due misure coincidono; noto anche che la base minore del trapezio ed il suo lato obliquo sono pari a due volte il lato del quadrato, e sulla base di queste informazioni ho costruito tre figure:
un aquilone o deltoide
un rettangolo
e un trapezio isoscele
Se non vale, "cancello" tutto...
Purtroppo, non vale caro Andy. Il quadrato deve essere sistemato in una certa posizione e solo dopo si traccia la linea divisoria. Considera, in pratica, che il quadrato si debba incollare e ottenere una certa figura divisibile in due parti uguali.
Oltretutto mi sembra che la diagonale del quadrato non sia uguale alla base minore del trapezio...
Ok, cancello tutto.
Però avevo scritto che la base minore del trapezio è due volte il lato del quadrato, non la sua diagonale..
Ma, allora, da dove salta fuori il triangolo azzurro dell'aquilone? La figura deve essere ottenuta con il trapezio e il quadrato... Insomma, non cin siamo capiti, ma resta il fatto che l'unica cosa che si può fare e accostare (incollando) in qualche modo il quadrato al trapezio, comporre così una nuova figura (UNICA) e solo a questo punto dividerla in due parti uguali.
Scusa Enzo, dal disegno originale sembra che lato obliquo e base minore del trapezio siano lunghi uguali e che il lato del quadrato sia lungo la metà degli stessi... giusto?
giusto!
Caro Enzo è un po' che volevo rispondere, magari poi mi sbaglio, ma non ho avuto il tempo di fare un disegno.
Provo a spiegarlo a parole.
Io farei coincidere l'angolo superiore destro del trapezio con l'angolo inferiore sinistro del quadrato.
Pertanto partendo dall'angolo inferiore sinistro del trapezio seguo la sua diagonale fino all'angolo superiore destro.
Tale linea di divisione prosegue come diagonale del quadrato dal suo angolo inferiore sinistro fino al suo angolo superiore destro.
In questo modo presumo che tale linea formata dalle diagonali del trapezio e del quadrato divida in due figure uguali, sovrapponili ruotandone una delle due di 180°.
Se ho capito bene la tua proposta, tu taglieresti il trapezio con una diagonale (a parte il quadrato), ma essa NON divide a metà il trapezio, le due parti sono nettamente diverse...