Due costruzioni dell'ellissi sembrano del tutto scorrelate e, invece...

Quando nel corso di matematica abbiamo parlato delle coniche e, in particolare, dell'ellisse, abbiamo mostrato la sua costruzione classica, usando uno spago legato ai due fuochi e la matita che gli gira attorno.  A partire da questa caratteristica avevamo derivato la sua equazione cartesiana. Tuttavia, sappiamo anche che l'ellissi si riesce a ottenere tagliando un cono con un coltello (da cui proprio il nome di "coniche"). Le due costruzioni sembrerebbero non avere nulla in comune e, invece, dicono praticamente la stessa cosa.

E' interessante dimostrare questa conclusione. Partiamo dal nostro cono e inseriamo due sfere, una più piccola vicina al vertice del cono e una più grande nella parte inferiore. Le due sfere sono tangenti internamente al cono ma non si toccano fra loro. Non è difficile tracciare un piano p che tagli il cono e sia anch'esso tangente alle due sfere. Lo mostriamo in Fig. 1, con una visione piana.

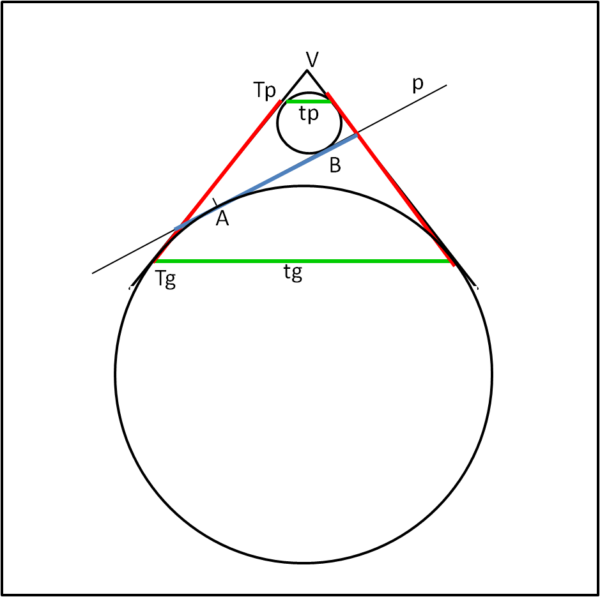
Le circonferenze verdi (tp e tg) sono il luogo dei punti di tangenza del cono con le due sfere. I punti A e B sono i punti di tangenza del piano p con le due sfere. Il segmento azzurro individua l'ellisse in quanto corrisponde alla sezione del cono da parte del piano p. Vediamo la stessa figura (Fig. 2) in tre dimensioni...

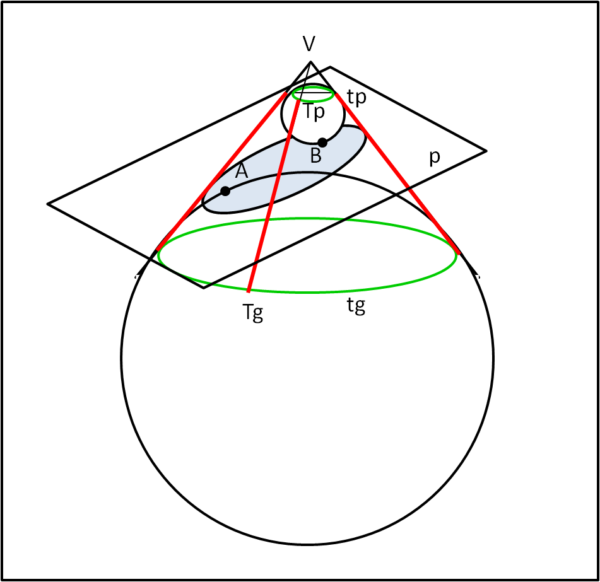
Notiamo subito un fatto banale, ma decisivo: i segmenti rossi, come Tp Tg sono tutti uguali tra loro, dato che uniscono punti di circonferenze poste su piani paralleli, aventi centro sulla stessa retta perpendicolare ai piani. A e B li ipotizziamo essere i fuochi dell'ellisse azzurra (dobbiamo dimostrarlo...).

I segmenti rossi, tutti uguali tra loro, possono essere divisi in due parti dalla ellisse. La somma delle due parti deve comunque essere sempre costante. Consideriamo, allora, un punto dell'ellisse Q nella Fig. 3.

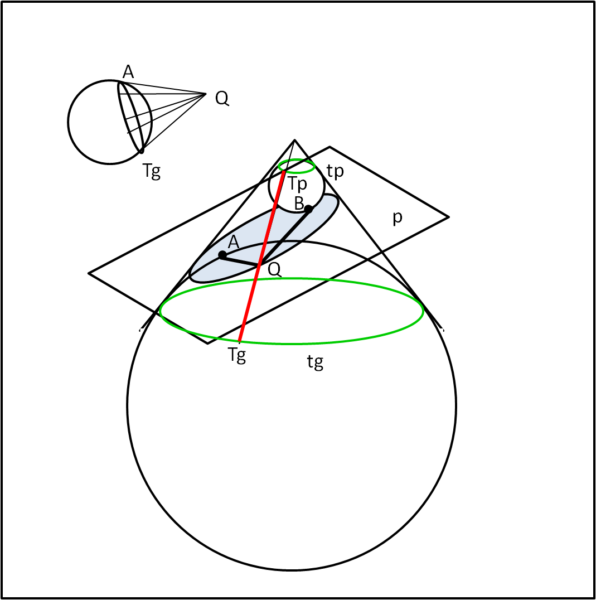
I segmenti QA e QTg devono essere uguali tra loro, dato che sono due tangenti tracciate da un punto esterno (Q) a una sfera (Tg e A appartengono entrambi alla sfera grande), come mostra la figurina in alto a sinistra. Uguale situazione si ha per QB e QTp.

Possiamo allora scrivere:

QTg + QTp = costante

e, quindi, anche:

QA + QB = costante

In poche parole la somma delle distanze di un punto dell'ellisse da due punti detti fuochi rimane costante: attraverso la costruzione con il coltello abbiamo trovato esattamente la costruzione con lo spago.