(QI) Dividere un cerchio in 7 parti di uguale area con riga e compasso *** (NEW!)

24/08/22

(QI) Dividere un cerchio in 7 parti di uguale area con riga e compasso *** (NEW!)

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:12

N.B.: Ho corretto il quiz, dato che non si vogliono sette parti uguali, ma sette parti di uguale area...

Le costruzioni "classiche" attraverso una riga non graduata e un compasso (che non può essere usato come misuratore di una distanza) mi hanno sempre affascinato. Ecco quindi un "quiz" che torna su questa problematica tanto cara agli antichi greci.

Abbiamo già visto che Gauss (e non uno qualsiasi) ha dimostrato che non tutti i poligoni regolari sono costruibili esattamente con riga e compasso. Tra questi vi è l'eptagono. Su questo argomento ci siamo già dilungati anche evidenziando come certe costruzioni proposte sul web siano solo approssimate.

Ed ecco allora la nostra richiesta:

Come dividere esattamente un cerchio in sette parti di uguale area?

La faccenda si risolverebbe facilmente per un numero n minore di 7. Se n fosse uguale a due basterebbe dividere a metà il cerchio. Per n = 3, 4, 5 e 6 basterebbe costruire il corrispondente poligono regolare utilizzando riga e compasso (Gauss lo conferma!) e poi unire i vertici con il centro del cerchio. Nella figura che segue vediamo la divisione in 6 parti grazie all'esagono regolare inscritto.

Banale, direte... Beh lo possiamo fare anche con l'ettagono? No, dato che l'ettagono non è costruibile con riga e compasso. Come potremmo allora risolvere il problema?

QUI la soluzione

Articoli correlati

12 commenti

  1. Vincenzo Zappalà
    27/08/2022 at 11:46

    Chiedo scusa a tutti... Ho scritto parti uguali, ma intendevo parti aventi la stessa area. Penso che adesso il silenzio si trasformi in tante risposte!

  2. Francesco
    27/08/2022 at 19:14

    Premetto che non sono arrivato fino in fondo, ma ho solo fatto il seguente ragionamento.

    Esclusa la costruzione di un ettagono (che dovrebbe essere per forza essere regolare data la richiesta di aree uguali) mi pare che ci resti solo la divisione del cerchio o tramite rette parallele o tramite corone circolari. Credo che tramite corone circolari si riescano a costruire i 6 raggi richiesti con riga e compasso ponendo

    0=r_{0}<r_{1}<r_{2}<r_{3}<r_{4}<r_{5}<r_{6}<r_{7}=R

    dove R è il raggio del cerchio dato.

    L'area della corona circolare An+1 compresa tra i raggi rn+1 e rn è A_{n+1}=\pi (r_{n+1}^{2}-r_{n}^{2}).

    Imponendo l'uguaglianza delle aree avremo per ogni n<7

    (r_{n+1}^{2}-r_{n}^{2})=(r_{n}^{2}-r_{n-1}^{2}), cioè

    2r_{n}^{2}=r_{n+1}^{2}+r_{n-1}^{2}, quindi esplicitando

    2r_{1}^{2}=r_{2}^{2}

    2r_{2}^{2}=r_{3}^{2}+r_{1}^{2}

    ....

    2r_{6}^{2}=r_{7}^{2}+r_{5}^{2}

    ma r7=R, quindi tornando indietro riusciremo a scrivere r6 come somma di quadrati di r5 e R, r5 come somma di quadrati di r4 e R... e infine r2 come somma di quadrati di R, da cui poi tornando avanti trovo tutti gli rn.

    Poiché mi risulta che la somma di quadrati e le radici quadrate siano costruibili con riga e compasso, mi pare che con parecchio sudore si possa risolvere il problema.

    MOLTO probabilmente si può fare di meglio, ma intanto ci ho provato :-)

     

  3. Francesco
    28/08/2022 at 07:11

    Certo che son bravo a complicarmi la vita! :-)

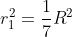    Non solo so che le aree delle corone circolari devono essere uguali tra di loro, ma so anche quanto vale l'area di ogni corona circolare: A_{n}=\frac{\pi }{7}R^{2}, quindi r_{1}^{2}=\frac{1}{7}R^{2}  e da (vedi sopra) 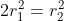2r_{1}^{2}=r_{2}^{2}  viene r_{2}^{2}=\frac{2}{7}R^{2}.

    Poi, usando le relazioni scritte sopra, seguono tutti gli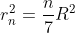  r_{n}^{2}=\frac{n}{7}R^{2}, tutti costruibili con riga e compasso, se non sbaglio di grosso.

     

  4. Vincenzo Zappalà
    28/08/2022 at 07:16

    Attenzione... se conosci una lunghezza NON puoi usare il compasso per riportare quella lunghezza. Il compasso può solo essere usato facendo centro in un punto e aprendolo in modo che tocchi un altro punto. Non si può aprire di una lunghezza prefissata. Sempre che abbia capito bene il tuo approccio... Comunque sì, si può fare in altro modo, senza troppi calcoli.

    In ogni modo, caro Francesco, mi congratulo con te per la passione che dimostri!

  5. Francesco
    28/08/2022 at 08:29

    Accidenti, non ci arrivo mai in fondo! :-(

  6. Vincenzo Zappalà
    28/08/2022 at 10:00

    Ricordati Talete... lui sapeva fare una cosa molto importante!

  7. Vincenzo Zappalà
    29/08/2022 at 10:55

    Mi spiace che questo quiz rimanga insoluto... aspetto ancora oggi e poi riporto la soluzione (ma ce ne possono essere anche altre...).

  8. Andy
    29/08/2022 at 17:26

    Caro Enzo,

    dopo aver letto i tuoi articoli

    http://www.infinitoteatrodelcosmo.it/2021/12/08/come-costruire-un-poligono-regolare-di-n-lati-qualsiasi-con-riga-e-compasso-seconda-parte/

    http://www.infinitoteatrodelcosmo.it/2022/01/06/come-costruire-un-poligono-regolare-di-n-lati-con-riga-e-compasso-seconda-parte/

    ho pensato di usare un metodo di disegno tecnico per disegnare un poligono regolare di n lati inscritto in una circonferenza, con il vincolo di NON usare il compasso per riportare misure:

    traccio una retta s orizzontale e in un suo punto qualsiasi, con il compasso disegno una circonferenza di raggio qualunque; traccio l'asse del diametro orizzontale per disegnare il diametro verticale (punto d'incontro O);

    traccio una retta tangente alla circonferenza in O'' (color oro) e, scelto un quadrato di lato qualunque, lo riporto affiancato 7 volte;

    traccio una linea rossa tratteggiata a partire dallo spigolo più distante del quadrato più esterno sino al punto O', le successive linee rosse tratteggiate sono tutte parallele al prima rossa e intercettano il diametro verticale in 8 punti o nodi (si potrebbero numerare partendo da O' = nodo 0 (zero) sino a O'' = nodo 7), dividendo così lo stesso diametro verticale in 7 parti uguali;

    ho contrassegnato i nodi pari con una tacchetta e i dispari con un pallino;

    ho poi tracciato l'asse del raggio OO'', che intercetta la circonferenza nei punti C e C', disegnando i raggi OC e OC'; ma dato che OM è pari a metà raggio, il raggio OC e il raggio orizzontale racchiudono un angolo θ di 30° (OM è pari al raggio per il seno di 30 che è 1 / 2), stesso discorso per il raggio OC';

    traccio una retta t tangente alla circonferenza nel punto O', e da O' disegno una linea parallela al raggio OC che intercetta la retta s nel punto P; simmetricamente trovo il punto P';

    da P disegno delle direttrici verdi passanti per i nodi dispari che intercettano la circonferenza (dalla parte più distante a P) in 4 punti; simmetricamente dal punto P' partono delle direttrici viola passanti sempre per gli stessi nodi dispari, che intercettano la circonferenza in altri 4 punti.

    Unendo consecutivamente i punti segnati dalle frecce verdi e viola si ottiene un eptagono inscritto che, se regolare, suddivide il cerchio in 7 settori circolari di pari ampiezza.

     

    P.S.

    ho provato, a parte, a disegnare l'eptagono, partendo da un lato e facendo perno su un estremo, per ruotarlo sino ad intercettare il punto successivo, e sembra che i 7 lati così ottenuti presentano uguale misura.

    Ho provato anche con un numero di lati maggiore e minore di 7 e sembra, ripeto sembra, funzionare.

  9. Vincenzo Zappalà
    29/08/2022 at 17:35

    caro Andy,

    devo leggerlo per bene... se tu avessi ragione smentiresti Gauss!!! 8-O 8-O

  10. Vincenzo Zappalà
    29/08/2022 at 18:35

    Va tutto bene, ma non mi convince l'ultima parte...

    Unendo consecutivamente i punti segnati dalle frecce verdi e viola si ottiene un eptagono inscritto che, se regolare, suddivide il cerchio in 7 settori circolari di pari ampiezza

    Chi mi dice che gli angoli al centro sono uguali?

  11. Andy
    29/08/2022 at 18:56

    Per questo l'ho scritto con il beneficio del dubbio.

    Una volta che le misure dei lati si ripetono costantemente, bisogna vedere se 2R sen(180/7) = L viene rispettata o meno, ma in ogni caso rappresenta una valore approssimato perché il seno di 180 / 7 potrebbe essere un numero irrazionale.

  12. Vincenzo Zappalà
    29/08/2022 at 19:02

    caro Andy,

    temo, infatti, che si cada nell'approssimazione come descritto qui:

    http://www.infinitoteatrodelcosmo.it/2022/01/06/come-costruire-un-poligono-regolare-di-n-lati-con-riga-e-compasso-seconda-parte/

    Ti posso assicurare che la soluzione è decisamente più semplice... Tu ce la puoi fare sicuramente!

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.