Questo articolo è inserito in "Sezione Aurea, spirali e altre forme ricorrenti nell'Universo"

 

Volevo scrivere un articolo sul diagramma di Voronoi, ma, come spesso capita, mi sono accorto di averlo già scritto... Poco male - ho pensato- e ho deciso di riproporvelo, aggiungendo un approfondimento sulla costruzione del diagramma di Voronoi. Contenendo anche una parte "pratica", potrebbe servire per passare il tempo durante le ferie.

Doveva essere una news, molto breve, è invece è diventato un articolo dai molti risvolti. Una scoperta veramente importante che ha avuto una scarsa eco, se non nei rispettivi campi scientifici. Un vero peccato e ho cercato di inserire il maggior numero di informazioni (a modo mio, ovviamente). Non l'ho voluto spezzare in due o più parti, proprio per creare quell'unità multidisciplinare che domina il tutto. Ci sarebbe comunque da parlarne ancora di più; è un po' come le noccioline: una tira l'altra!

Inizierò questo articolo con una delle mie solite favole (che i biologi mi perdonino!).

 

La favola della vita

Circa 3.5 miliardi di anni fa nasce la prima cellula, il primo essere vivente, ossia capace di recuperare energia da ciò che lo circonda e immagazzinarla per compiere azioni come, ad esempio, moltiplicarsi.

All'inizio, per mancanza di ossigeno, la faccenda è molto complicata e se non ci fossero particolari molecole come gli enzimi, servitori fedeli e rapidissimi, forse tutto finirebbe prima di cominciare. Che forma ha la prima cellula? Probabilmente quella di una piccolissima sfera (o di piattello circolare a due dimensioni). La Natura sa bene che questa forma ha dalla sua grandi vantaggi, se non altro quello di di "sprecare" la minima energia possibile. La nostra prima cellula si moltiplica, spezzandosi praticamente in due e la popolazione aumenta. Hanno tanto spazio a disposizione negli oceani e sono libere di vagare in lungo e in largo.

Sono organismi cacciatori che devono cercare il loro nutrimento, capace di donargli quel po' di energia in grado di farli evolvere. Evoluzione... che grande e bella parola. Ci ricorda ciò che è capitato alla specie umana.

 

La nascita della società organizzata

All'inizio, ogni singolo individuo fa di tutto: caccia, pesca, scova e/o costruisce ripari per la notte, accende fuochi per scaldarsi e per far paura agli animali che come lui cercano cibo, lotta con chi si avvicina troppo o invade il suo territorio di caccia.

E' meglio unirsi e formare delle tribù, dato che per catturare grosse prede è necessario essere in tanti. Probabilmente, qualcuno si dedica alla ricerca di frutta e di tuberi (i meno forti), mentre gli altri inseguono le mandrie delle prede. Un continuo vagare e c'è ben poco tempo per pensare e riflettere.

Poi, lentamente, nasce l'agricoltura e si comincia a capire che è molto meglio organizzare la tribù, sempre più grande, in modo che possa sistemarsi in un luogo stabile. Non c'è nemmeno bisogno che tutti sappiano fare tutto. Qualcuno pensa alla caccia, qualcuno alla pesca, qualcuno alla coltivazione, qualcuno a fare la guerra agli invasori, qualcuno a costruire le case, qualcuno a decorarle e, finalmente, qualcuno inizia ad avere tempo per pensare, studiare la Natura, inventare soluzioni, addirittura fare delle filosofia. Qualcuno, inoltre, dotato sia di particolare intelligenza che di furbizia, assume il comando, spesso approfittando di una sua posizione di forza.

Si verifica quella che può essere considerata la più grande conquista dell’umanità di tutti i tempi: la nascita dello Stato organizzato. Non tutti fanno tutto, ma i compiti vengono sapientemente separati.

Ci sono sicuramente anche gli "svogliati", gli inetti, quelli che non hanno voglia o non possono fare niente. Non è facile a quei tempi e chi riesce a farlo è costretto a isolarsi e a fare una vita meschina. Oggi questi gruppi esistono ancora, ma sono -a volte- composti da incapaci e "furbi" (a modo loro), abilissimi nel non fare praticamente niente (anche perché non ne sarebbero capaci), ma di riuscire ad assumere i ruoli più importanti nella comunità. Se poi tutto va a rotoli non c'è da stupirsi. Conosciamo tutti benissimo come vengono chiamati... ma torniamo alle nostre cellule.

 

La società perfetta delle cellule

Anche loro vogliono progredire e un po' alla volta si riuniscono in tribù. Ciascuna cerca di stare attaccata all'altra in modo da difendersi al meglio da attacchi esterni. E già la forma sferica comincia a non essere l'ideale: troppo spazio vuoto tra una e l'altra, spazio che potrebbe essere facilmente invaso. Meglio cambiare forma per cercare una maggiore unità.

 

Il diagramma di Voronoi: a ciascuna il suo spazio

La matematica e la geometria assumono un ruolo importante. L'esagono, soprattutto, diventa figura quasi perfetta: pensiamo agli alveari delle api e alle bolle di sapone che si uniscono (non mancano però anche i pentagoni...).

 

Più in generale, è particolarmente interessante a questo riguardo è il diagramma di Voronoi. La sua definizione sembrerebbe avere poco a che fare con le cellule degli esseri viventi:

Stabilito un certo numero di punti, che possiamo chiamare "semi", esiste attorno a ciascuno di loro una specie di "proprietà privata" che contiene tutti i punti che stanno più vicini al loro seme rispetto ad altri semi posti nei dintorni. Queste proprietà private possono essere chiamate celle o -se preferite- cellule (in inglese si usa la stessa parola, "cell"). I limiti delle celle sono segmenti che hanno la stessa distanza da due semi. Gli angoli delle celle sono punti che hanno la stessa distanza da tre semi (usando il piano euclideo, ma si potrebbe anche estendere la distanza ad altre geometrie...).

 

Approfondimento: Come costruire un diagramma di Voronoi

Cominciamo con due soli punti: basta unirli e tracciare la perpendicolare a questo segmento nel suo punto medio, come mostra la figura che segue:

 

Per come è stata costruita, la retta r è il luogo dei punti equidistanti da A e B. Ne segue che tutti i punti che stanno alla sua sinistra hanno una distanza da A che è minore di quella rispetto a B. La retta r divide lo spazio nelle due celle relative ad A e a B.

Aggiungiamo, adesso, un terzo punto C al digramma appena disegnato. Come si trasforma il nostro diagramma? Non è difficile ripetere l'operazione precedente tra A e C e tra B e C.

Abbiamo costruito le rette s e t relative ai segmenti BC e AC. Teniamo presente. che:

Ogni punto della retta r è equidistante da A e B

Ogni punto della retta  s è equidistante da B e C

Ogni punto della retta t è equidistante da A e C

Le due rette, s e t, si intersecano in un punto V. Quel punto ha la stessa distanza da A e C e da B e C. Ossia VB = VC = VA. Ma la retta r è il luogo dei punti equidistanti da A e B e quindi deve avere un punto U  tale che UA = UB, ossia U deve coincidere con V. Chiamiamo questo vertice V_ABC. Le tre rette ci forniscono le nuove celle, considerando soltanto le semirette che partono da V_ABC. In particolare, ogni punto P della retta s che si trova a sinistra di V_ABC deve essere annullato, dato che è sicuramente più vicino ad A che non a B e a C. Analogo discorso vale per ogni punto R che sta nella parte inferiore della retta r rispetto a VABC (in quella zona "comanda"  il nuovo arrivato C). Per concludere  si elimina anche il tratto della retta t che sta nella parte alta rispetto a VABC, dato che ogni suo punto è sicuramente più vicino a B. Il nuovo diagramma è delimitato dalle parti continue delle retta retta nera e delle due rosse.

Il gioco continua e aggiungiamo un punto D.

Ciò che importa è costruire il vertice V_ACD seguendo la solita procedura.  Come scegliere il nuovo vertice tra quelli possibili? Il nuovo punto D appartiene alla cella di C, e, quindi la prima cosa da fare è trovare la retta che separa i loro domini (retta u). Essa incontra sicuramente la retta t nel nuovo vertice V_ACD cercato. Da questo punto passa sicuramente anche la retta v che separa le celle di A e di D. Basta escludere il pezzo di t tratteggiato ed ecco la nuova divisione delimitata dalle rette rosse e azzurre continue. Ovviamente, non vi può essere nessuna divisione tra la cella di D quella di B. Posso assicurarvi che è molto più facile eseguire direttamente le operazioni piuttosto che cercare di descriverle a parole.

Possiamo concludere aggiungendo ancora un punto E al diagramma precedente.

Notiamo che il punto E si intrufola all'interno del vecchio diagramma e la sua cella influisce su tutte quelle precedenti. Nessun problema... il punto E si trova nella vecchia cella di C e quindi la prima cosa da fare è determinare il vertice V_ECD . Poi si passa a V_AED, a V_ABE e, infine, a VEBC. E' immediato escludere i tratti che non interessano, ossia quelli appartenenti sicuramente alla nuova cella di E.

Vediamone subito un esempio con un numero di punti ben più elevato. Rimane il fatto che i vertici delle varie celle rappresentano sempre le intersezioni di tre divisioni.

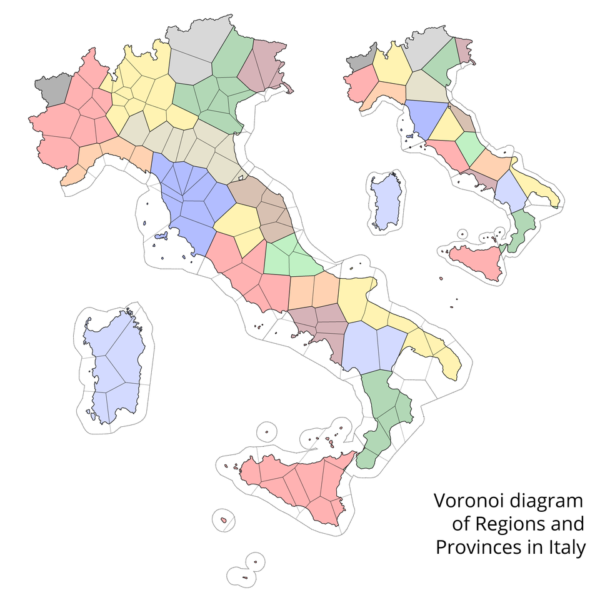
Se facciamo attenzione, ogni cella, colorata in modo diverso, contiene tutti i punti che hanno la distanza minima rispetto al loro seme. Senza passare a cellule, si potrebbe, ad esempio, considerare come "semi" le capitali delle regioni italiane (o i capoluoghi di provincia) e poi costruire le celle per ognuna di esse. La forma delle regioni e delle provincie sarebbe ben diversa da quella attuale.

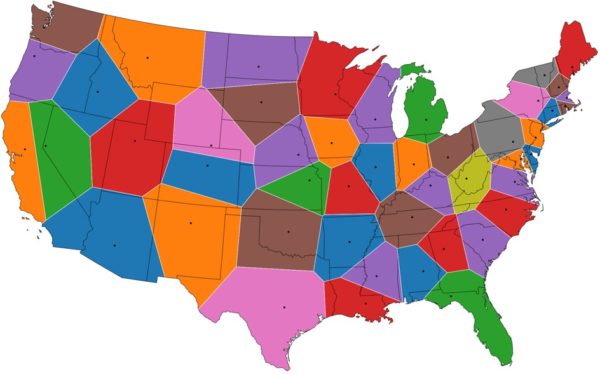
Anche per gli Stati Uniti è stato fatto, ed ecco il risultato:

Particolarmente interessante è vedere come la struttura diventi "dinamica". Ad esempio, inserendo un nuovo seme in movimento attraverso una popolazione di celle (cellule) già sistemate. Lo illustra molto bene il breve video che segue:

 

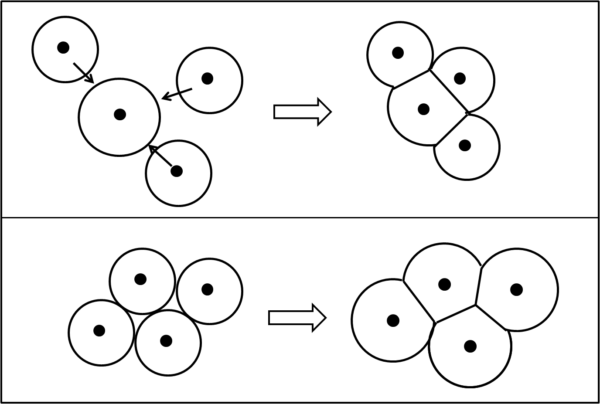
Per eliminare il nome cella e passare veramente a cellule, potremmo considerare due meccanismi molto semplificati, ma non assurdi. La figura che segue ne fa un semplice schema con pochissime cellule:

Tante cellule rotonde che si avvicinano (in alto), oppure tanti cerchietti che si gonfiano (in basso). Il seme è il loro centro (nucleo).

Possiamo facilmente estrapolare il tutto o, ancora meglio, andare a leggere questo articolo che discute proprio la struttura cellulare confrontandola con il diagramma di Voronoi. Di seguito una figura tratta dall'articolo, particolarmente esplicativa:

Torniamo alla evoluzione cellulare. Anche tra le cellule nasce il bisogno di costruire una vera civiltà. Bisogna crescere in numero, ma soprattutto bisogna che anche loro si specializzino: qualcuna deve pensare alla difesa esterna, qualcuna deve trasformare, altre devono distribuire, altre trasportare, altre costruire, altre assumere il cibo, altre recuperare l'ossigeno, altre, ancora, devono dirigere le operazioni. Insomma ognuna inizia a fare un lavoro diverso e diventa sempre più esperta.

Chi comanda tutto sono cellule che devono segnalare, decidere, manovrare, magari anche pensare, e molto altro ancora.

Veniamo finalmente al dunque della questione: tra le cellule ci sono quelle che devono creare uno scudo verso l'esterno e proteggere gli organi interni dove si svolgono i lavori più delicati e rischiosi. Non solo devono proteggere e quindi devono stare più unite possibile, ma devono anche essere capaci di muoversi secondo gli ordini che provengono dal centro direzionale. Devono sapersi adattare alla situazione nel loro complesso, ma, nel contempo, devono mantenere un'unità perfetta. In qualche modo, possiamo pensare allo spaziotempo curvo. Tanti piccoli "poligoni" capaci di adattarsi a ciò che dice la "massa", ossia il motore centrale, pensante. Tutti uniti, seguendo regole precise, che permettano una deformazione continua, capace di arrivare ai limiti più rischiosi, quando chi comanda il tutto ha un'energia fuori dal comune.

Insomma, stiamo parlando delle cellule epiteliari, quelle che formano la pelle, sempre a contatto con l'esterno e con condizioni di temperatura, pressione, interferenze con altri esseri viventi oppure no, sempre diverse e a volte molto critiche. Ma esse formano anche degli scudi protettivi per i macchinari più preziosi della società civile, non ultimo il sistema dei "canali" che distribuisce le sostanze primarie e l'energia a tutta la costruzione. No, nell'essere vivente complesso, multicellulare, non esistono i furbetti del quartierino e chi ha il comando è sempre il migliore, quello che lavora di più e con estrema rapidità. Ci stiamo accorgendo, però, che la rappresentazione disegnata su un piano non basta più e dobbiamo lavorare nelle tre dimensioni spaziali.

 

Un vero lavoro di squadra

Fino a qui, ho (s)parlato di biologia, con brevi accenni alle strutture geometriche più semplici, ma cosa succede quando i biologi vogliono cercare di capire la struttura e la forma particolare di quelle cellule così importanti per la difesa del nostro organismo? Studiano, elaborano modelli e poi chiedono aiuto a chi è specializzato in forme geometriche, più o meno vantaggiose per gli scopi biologici che vogliono ottenere.

I geometri disegnano, "inventano" soluzioni che siano di semplice descrizione, che possano semplificarsi in modelli standard e, non ultimo, che possano anche essere riprodotte in laboratorio. Per accettare certe forme chiedono, però, anche ai fisici per sapere se, in realtà, strutture geometriche che sembrano perfette da un punto di vista teorico e che andrebbero bene ai biologi, abbiano anche un significato fisico particolare.  Un po' come un architetto che sa disegnare una costruzione di bellissima estetica, ma che chiede agli ingegneri se può stare "in piedi" (sembra che Leon Battista Alberti fosse un po' così...).

In altre parole, bisogna dimostrare che una certa forma riesca a fare spendere meno energia, a permettere il massimo risultato con il minimo sforzo, essere in grado di rispondere al meglio agli ordini superiori. Sintetizzando, oltre che essere bella e perfetta geometricamente deve anche avere un valore fisico tale da averla fatta preferire dalla Natura (e quindi essere visibile ai biologi).

Una collaborazione importantissima tra tre discipline che lavorano in modo egregio e senza cercare di ostacolarsi per prevalere. Risultato? Una nuova forma geometrica, fantastica nella sua semplicità e nelle sue possibilità di utilizzo: lo SCUTOIDE. L'uomo l'ha scoperta solo nel 2018, ma non si inorgoglisca troppo: la Natura l'aveva già scoperta da miliardi di anni... Si parla spesso di scoperte, ma spesso non sono altro che comprensione della Natura (Galileo insegna). In altre parole, il pi greco non è stato ideato dall'uomo, ma dalla realtà che esisteva ben prima di lui. Lo scutoide è stato evidenziato, ma la Natura sembra dire: "Era ora che lo capiste!".

Sto scherzando (in parte) ma l'individuazione di una forma geometrica, così amata e seguita dalle cellule viventi "civilizzate" e "socialmente evolute" resta una conquista veramente eccezionale, capace di descrivere (e magari di ripetere in laboratorio) i moduli elementari per costruire, attraverso le tecniche più raffinate, delle perfette riproduzioni del tessuto epiteliare. Stranamente (ma spesso capita quando si scontrano interessi diversi, dato che la società umana è ben più rozza e impreparata rispetto a quella naturale -pensiamo anche solo a come una immensa colonia di virus sappia organizzarsi meglio della civiltà tecnologica odierna-) è passata quasi del tutto inosservata, quasi fosse solo un giochino geometrico.

E' venuta l'ora di darle il giusto risalto. Lo faremo dirigendoci principalmente verso la sua parte essenzialmente geometrica, dato che la biologia non è certo il mio campo. Tuttavia, per capire la perfetta connessione tra cellule viventi e forme geometriche, è fondamentale questo articolo, quello da cui tutto è partito.

 

Costruiamo lo scutoide

Cerchiamo di descrivere la costruzione tridimensionale (non banale!) e le varianti  più complesse che possono avvicinarsi sempre più alla realtà delle vere cellule viventi.

Il prismatoide

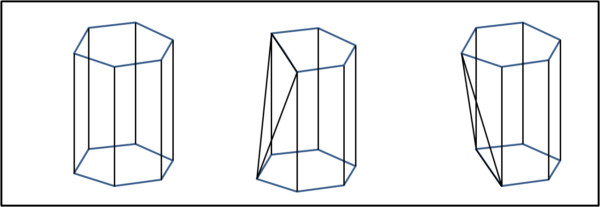
Tutti sappiamo cos'è un prisma. Nel caso più regolare, ad esempio, basta prendere due figure piane regolari uguali, come due esagoni (l'esagono è una forma piana molto amata dalla Natura, come già detto), che stiano su due piani tra loro paralleli e unire i vertici con rette giocoforza anch'esse parallele. La massima regolarità si ha, ovviamente, quando le rette che formano il "corpo" del prisma, sono perpendicolari ai due piani degli esagoni:

A sinistra un prisma retto, in cui le facce laterali sono rettangoli; a destra un prima obliquo, in cui le facce laterali possono essere anche  parallelogrammi.

Prendiamo adesso il nostro prisma, anche perfettamente regolare, ma rimpiccioliamo la faccia superiore mantenendola del tutto simile a quella inferiore. Otteniamo un tronco di piramide. Potevamo costruirlo molto più facilmente considerando una piramide vera e propria e poi tagliarla con un piano parallelo a quello di base. Abbiamo preferito definirlo in modo diverso proprio per associarlo ancora meglio al prisma. Un tronco di piramide è un prisma che ha le due basi sempre parallele, ma di dimensioni diverse. Ci verrà utile tra poco...

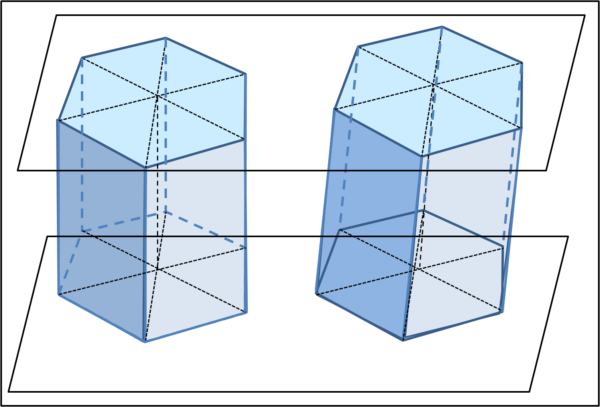
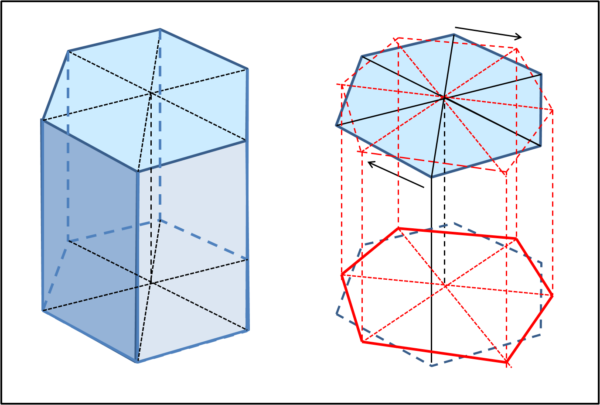
Manteniamo, per adesso,  i nostri esagoni uguali e su piani paralleli, ma divertiamoci a ruotarne uno dei due di un certo angolo come mostra la figura che segue:

Una manovra molto facile... ma come si sistemano gli spigoli verticali? Non possono più dar luogo a semplici rettangoli e, se vogliamo che la superficie sia composta sempre da piani, siamo costretti a creare una superficie laterale fatta da triangoli, come illustrato di seguito.

Perfetto (direi). Come lo chiamiamo un solido del genere? Beh... è stato scelto antiprisma.

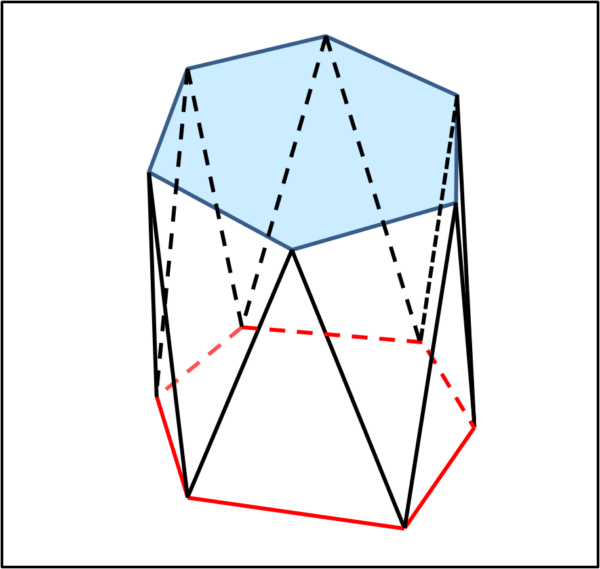
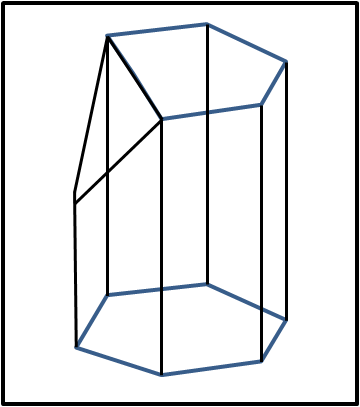
Facciamo un passo ulteriore, considerando il caso più semplice. Prendiamo il prisma originale, regolare, con basi due esagoni uguali e facciamo diventare quello superiore (o inferiore) un pentagono, saltando un vertice. Il solido resta a facce piane, ma per completarlo dobbiamo utilizzare un triangolo. Alla fine abbiamo una specie di mix tra un prisma e un antiprisma... Non ci resta che chiamarlo prismatoide.

Tuttavia, possiamo anche cambiare leggermente le cose proseguendo con lo spigolo verticale dell'esagono, che non trova il vertice corrispondente sopra (o sotto di sé) di sé, e poi (a metà strada, per esempio) fare intervenire la faccia triangolare. Bene, ci siamo! La figura ottenuta si chiama SCUTOIDE ed è proprio quella preferita dalla Natura per le sue cellule epiteliari.

E'  particolarmente interessante guardare questo breve video che anticipa e illustra certe semplici proprietà geometriche, presentato proprio da uno degli autori della ricerca (che, oltretutto, ha un volto veramente simpatico) che descrive i collegamenti più significativi tra biologia e geometria.

 

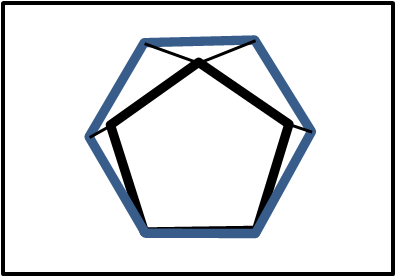
In realtà, quanto mostrato è un caso molto semplice, il più immediato e intuitivo degli scutoidi. Possiamo fare molto di meglio (e di più complicato), per avvicinarci al modello utilizzato dalla Natura. Consideriamo ad esempio una base esagonale e l'altra pentagonale, ma in modo tale che sia l'esagono che il pentagono abbiano i lati uguali. Un qualcosa, che visto dall'alto, mostra pentagono ed esagono con un lato sovrapposto.

 

Ovviamente, l'area del pentagono è più piccola di quella dell'esagono e, quindi, interviene nel gioco anche una specie di tronco di piramide (si parte dal grande e si restringe il tutto). Ovviamente, vogliamo sempre mantenere i poligoni su due piani paralleli. La faccenda si complica di molto e non è certo facile descrivere la costruzione di un qualcosa che comincia a non avere più le facce esterne piane.

Il video che segue mostra questa costruzione in modo puramente geometrico ed è la migliore che ho trovato in circolazione, ma penso che i nostri "maestri" di geogebra possano anche fare di meglio...

 

Se poi qualcuno volesse passare alla "pratica" e costruirsi un vero scutoide in tre dimensioni, consiglio vivamente di usare questo disegno. Basta ritagliare e incollare e il nostro solido nasce facilmente.

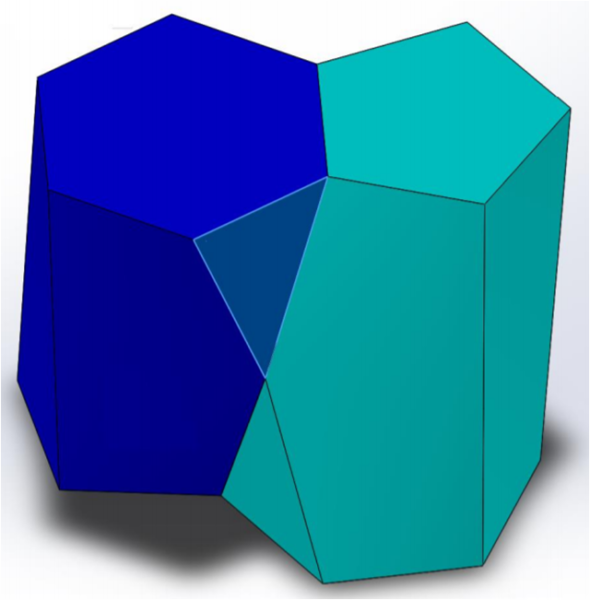
A questo punto si può già notare la peculiarità del "nuovo" solido: se ne prendiamo due, e ne ribaltiamo uno, è estremamente facile far coincidere due facce e avere l'incastro desiderato, tanto amato dalle cellule:

Tuttavia, nessuno ci vieta di modificare i poligoni, cambiando il rapporto tra area del poligono superiore e inferiore, passando anche a poligoni irregolari... magari seguendo il diagramma di Voronoi. Vediamo due scutoidi perfettamente complementari con basi diverse, in cui si notano bene le superficie curve (il triangolo e le basi restano comunque piane)

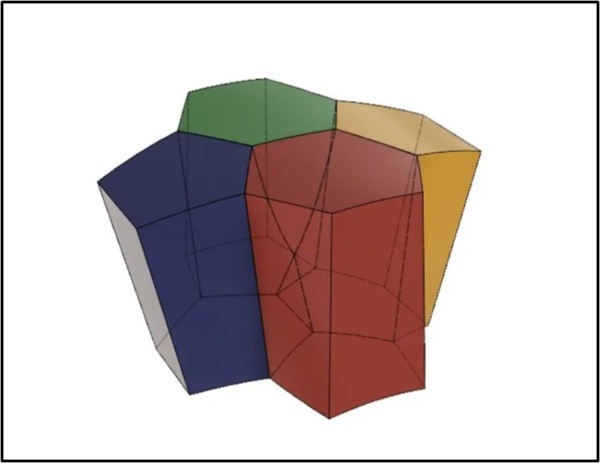
Possiamo vedere anche la combinazione di 4 scutoidi tali da creare una struttura curvilinea.

Anche di questa configurazione  è possibile ottenere una costruzione pratica, ritagliando e incollando:

Si può proseguire con sempre maggiore varietà...

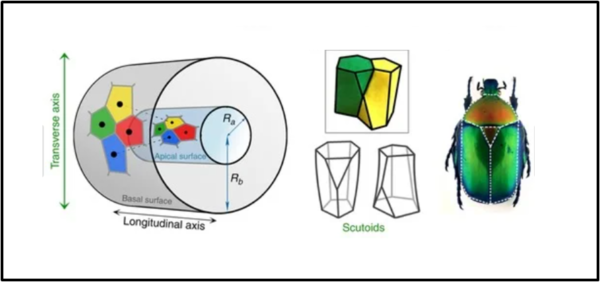
Ma, entrando con discrezione nel campo biologico, possiamo anche pensare ai canali che portano il sangue, a sezione circolare. Per dimostrarlo basta vedere una figura estratta dall'articolo originale che fa riferimento ai vasi sanguigni e alla loro struttura cilindrica, con un riferimento non troppo nascosto alle celle di Voronoi, per quanto riguarda le basi. A destra della figura vi è la spiegazione ufficiale del nome "scutoide": la sua forma assomiglia in qualche modo a quella del carapace di certi insetti.

Tuttavia, il nome ha una storia più lunga e simpatica. Appena scoperto, gli è stato dato il nome del leader del gruppo di ricerca, Escudo, e, quindi, Escudoide. Poi, però, si è preferito non esagerare con riferimenti troppo personali (le cellule che lo conoscono da miliardi di anni potrebbero alterarsi un pochino...) e siamo passati a Escutoide; infine è stata tolta anche la E, dando il massimo spazio all'insetto con quello strano "vestito".

I lavori proseguono nei tre campi e le possibilità che offrono sono ancora solo parzialmente conosciute.

In caso di novità, ci risentiamo!

 

A proposito di cellule QUI parliamo dei precursori neurali: cellule cilindriche che evolvono in modo diverso a seconda del tempo impiegato per riprodursi