Questo articolo è inserito in Dinamica e Meccanica

 

In questo articolo descriviamo e cerchiamo di spiegare (per quanto possibile) tre apparenti paradossi della fisica. Essi portano a risultati controintuitivi rispetto alle leggi fisiche comunemente accettate. In due casi, infatti, sembra che si possa eliminare o, almeno, contrastare la forza di gravità, in un terzo sembra potersi annullare la forza centrifuga.

 

La catena di maccheroni

Prendiamo una lunga catena formata da tanti tubicini rigidi collegati tra loro da un filo flessibile. Qualcosa simile alla figura che segue, come se fabbricassimo una catena di "maccheroni". Bene riempiamo un contenitore abbastanza alto con questa catena e poi prendiamo un capo della catena e lo portiamo fuori dal contenitore in modo che la forza di gravità lo faccia scendere verso il basso. Ci aspetteremmo, ovviamente, che a mano a mano che la catena inizia a scendere essa si porti con sé il resto della catena soggetta alla forza di gravità della parte libera di cadere il cui peso aumenta sempre di più.

Insomma ci aspetteremmo qualcosa come è raffigurato nella parte sinistra della figura che segue...

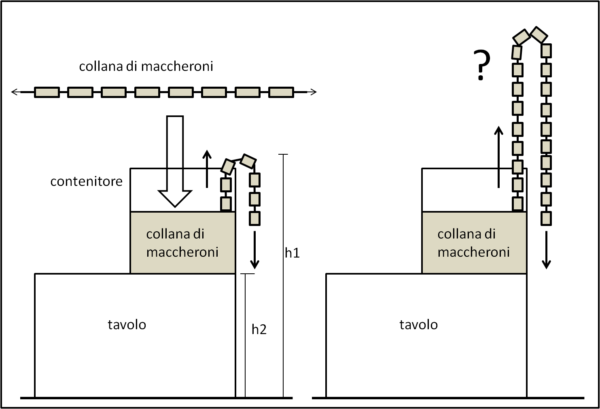
E, invece, no! La catena, prima di cadere verso il basso, si solleva rispetto all'orlo del contenitore come fosse una fontana che zampilla (parte destra della figura).

Vediamo anche un video che mostra quello che succede.

Si osserva, inoltre, che se aumenta l'altezza del contenitore rispetto al suolo, la fontana di tubicini sale sempre più in alto.

Questo apparente paradosso fisico o, quantomeno, questo effetto del tutto controintuitivo era già noto fin dalla metà del diciannovesimo secolo, ma è stato portato alla ribalta in una trasmissione televisiva della BBC condotta da Steve Mould , da cui il nome di "effetto Mould". La spiegazione è tutt'oggi ancora controversa, ma quella più calzante sembra essere quella fornita da due accademici dell'Università di Cambridge.  Cerchiamo di darne una spiegazione qualitativa lasciando l'analisi quantitativa all'articolo da loro pubblicato sul giornale della Royal Society.

Il tubicino che si solleva e raggiunge il bordo non ha nessun motivo logico di salire  più in alto dell'orlo, a meno che la non abbia subito una forza ulteriore. Ma dove si origina questa forza? Non certo nell'orlo del contenitore, ma proprio nella parte di catena che sta ancora dentro il contenitore. Vediamo, allora, cosa succede alla parte di catena che sta per essere trascinata verso l'orlo. La forza che trascina l'ultimo tubicino che si è sollevato, trascina anche quello successivo come è mostrato nella parte alta della figura che segue.

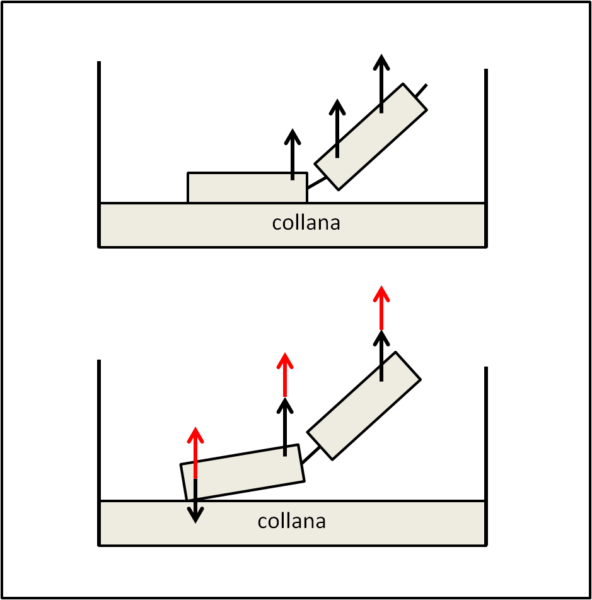
Tuttavia, lo solleva nella sua parte destra, costringendolo a ruotare attorno al suo centro di massa (in basso nella figura). La parte di sinistra, però, batte contro la catena ancora a riposo e subisce, perciò, una forza di reazione (rossa) che lo spinge verso l'alto. Ne segue che il tubicino viene sollevato a velocità maggiore di quella che avrebbe qualora fosse stato soltanto trascinato dalla forza di gravità della catena che cade oltre il bordo.

N.B.: ho usato i "maccheroni, in quanto costituiscono un elemento rigido soggetto a una coppia. Normalmente si vede una catena di palline, ma esse sono tenute insieme  in modo da formare anch'esse un sistema rigido a due a due. La stessa cosa non capiterebbe se avessimo una catena formata da palline attraversate da un filo flessibile, in quanto la pallina che inizia a salire potrebbe ruotare senza esercitare nessuna coppia su quella successiva. Questo tipo di catena, che non causa nessuna "fontana" è stata proprio usata per confermare l'ipotesi precedente.

Un processo dinamico veramente intrigante e controintuitivo attorno al quale non c'è ancora unanimità di pensiero. Fatto sta, però, che la fontana funziona!

 

Il pendolo di Kapitza o pendolo inverso

Il pendolo "inverso" di Kupitza era stato già proposto all'inizio del ventesimo secolo, ma si deve al premio Nobel Pyotr Kapitza una sua descrizione analitica che risale al 1951.

Vediamone le caratteristiche essenziali nella figura che segue:

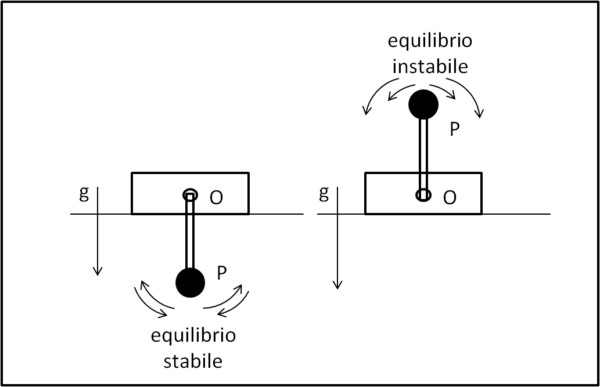
Il pendolo è composto da un'asta rigida con un peso P al suo bordo inferiore. L'asta può ruotare di 360 gradi attorno al suo punto di sospensione O che sta su un certo basamento. Ovviamente, l'unico punto di equilibrio stabile del pendolo è quella con il peso in basso, dove qualsiasi spostamento da questa configurazione riporta velocemente il pendolo nella condizione iniziale. Esiste anche una configurazione di equilibrio instabile, quella in cui il peso è posto nella parte superiore, esattamente sulla verticale rispetto al punto di sospensione. In questo caso, basta un piccolissimo spostamento per far ricadere il pendolo nella posizione iniziale col peso in basso.

Cosa succederebbe, però, se il basamento contenente il punto di sospensione si mettesse a vibrare in senso verticale? Se la frequenza della vibrazione fosse abbastanza alta ecco che la posizione di equilibrio instabile del pendolo diventerebbe l'unica stabile e tutti gli sforzi per farlo cadere verso il basso risulterebbero vani. Il bello è che questa "strana" stabilizzazione funziona anche con un pendolo doppio o triplo, come mostra il video che segue:

Un risultato davvero controintuitivo, la cui importanza, però, è enorme, avendo dato il via alla meccanica vibrazionale, capace di raggiungere equilibri dinamici mai ipotizzati prima. La trattazione analitica va oltre il livello di questo Circolo, ma per chi la volesse affrontare, consiglio questo articolo che, in qualche modo, la rende leggermente più semplice...

 

Il vortice inverso

Quest'ultimo apparente paradosso vede , tanto per cambiare, lo "zampino" di Einstein che ne ha dato, per primo, una spiegazione fisica.

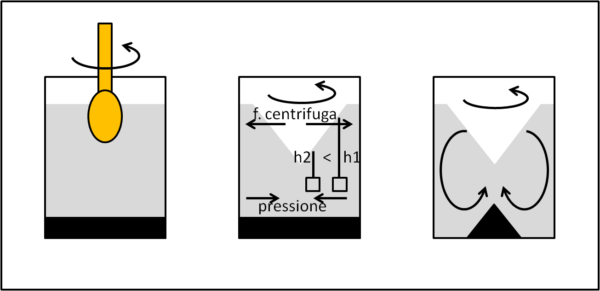
Sappiamo tutti come funziona una centrifuga. Mettendo in veloce rotazione delle provette contenenti liquidi di diversa densità, abbiamo una veloce separazione tra di essi: quelli più pesanti si porteranno verso le parti esterne delle provette. In qualche modo è un metodo che velocizza un processo altrimenti molto più lento. Se poniamo due liquidi a diversa densità in un bicchiere, dovremmo aspettare un po' di tempo prima che quello più pesante si depositi sul fondo. Tuttavia, se introduciamo la forza centrifuga attraverso la rotazione del liquido ecco che molto velocemente vedremo il liquido più pesante confinato ai bordi del contenitore. Pensiamo anche solo a un contenitore con dentro dell'acqua posto in rotazione: l'acqua tende ad andare verso il bordo del contenitore seguendo una curva ben nota a tutti.

Sulla base di questa esperienza ben nota, poniamo una sostanza più densa all'interno di un contenitore pieno d'acqua. Per rendere il tutto più evidente non ruotiamo il contenitore, ma solo il liquido al suo interno per mezzo, ad esempio, di un cucchiaino. Quest'azione causa qualcosa di inaspettato e controintuitivo:  al vortice che si osserva nella superficie superiore corrisponde una piccola montagna nella parte inferiore, in la sostanza più pesante si concentra verso il centro, proprio l'opposto di una centrifuga!

Vediamo, allora, come funziona l'intera faccenda... Cosa succede a un liquido in rotazione? Beh... lo sappiamo bene. Vediamo la situazione dall'alto e consideriamo cosa capita a un piccolo elemento di liquido dL. Esso subisce una velocità che lo porterebbe a sbattere contro il bordo del contenitore. Questa velocità, però, può essere  controbilanciata da una  accelerazione centripeta causata da una forza che punta verso il centro. Capita così che l'elemento di liquido si metta in rotazione "orbitando" attorno all'asse centrale. Ciò capita se tra accelerazione centripeta e velocità tangenziale esiste la ben nota relazione:

a = v²/r

dove r è la distanza dall'asse di rotazione.

Cosa succede se la velocità è, invece, più alta o più bassa? Beh... nel primo caso l'elemento parte per la tangente, ossia va a sbattere contro il bordo e viene trattenuto nel contenitore solo dalla presenza del suo bordo  e ivi si accumula, mentre nel secondo caso l'elemento cade verso il centro. Proprio ciò che avviene a un pianeta attorno alla sua stella. Tutto perfetto finora... Vediamo, adesso, la situazione  su un piano verticale. Nella parte superiore è presente un vortice di forma conica (o meglio con sezione parabolica) o giù di lì, proprio ciò che ci aspettiamo da un liquido in rotazione. Quello che importa è però la distanza del nostro elemento dL rispetto alla superficie superiore. La colonna di liquido che lo sovrasta determina la pressione a cui è soggetto l'elemento. Quello posto più lontano dal centro subisce, perciò, una pressione maggiore. Pressione maggiore significa movimento verso la zona di pressione minore, ossia una forza diretta verso il centro. Tuttavia, l'accelerazione che ne consegue è perfettamente bilanciata dalla velocità di rotazione. La pressione dipende solo dall'altezza della colonna di liquido, perciò la differenza di pressione si manterrà identica anche nel liquido posto in fondo al contenitore, quello più denso. Ciò implica che l'accelerazione verso il centro non cambia, però cambia la velocità dell'elemento a causa dell'attrito contro il fondo del contenitore. Ma, se diminuisce la velocità, abbiamo visto che il liquido tende a cadere vero il centro, formando così proprio il vortice inverso.

Tale fenomeno è noto come paradosso delle foglie di tè, e fu risolto nel 1926 da Albert Einstein, genio veramente poliedrico. Quando si mescola il tè nella tazza, si può vedere che si  forma un mulinello, un piccolo vortice superiore. Infatti, non appena incomincia a circolare, il liquido viene spinto verso l'esterno dalla forza centrifuga, esattamente come nel caso classico e intuitivo. Ripetiamo il ragionamento, seguendo Einstein (non fa mai male ripetersi...).

In un moto circolare le parti più esterne (più lontane dal centro di rotazione) si muovono più velocemente di quelle più interne, semplicemente perché devono percorrere più spazio nello stesso tempo: la velocità del liquido vicino ai bordi del contenitore è quindi maggiore di quello al centro. La forza centrifuga, però, dipende dalla velocità e il liquido al centro del contenitore sperimenta una forza centrifuga minore rispetto a quella che viene esercitata vicino ai suoi bordi che, impedendone la fuoriuscita, provoca un’innalzamento del livello superficiale vicino ad essi, mentre il liquido si “abbassa” verso il centro del contenitore (la forma della superficie è quella di una parabola). Otteniamo così il vortice superiore.

Ora, però, come in acque più profonde la pressione esercitata dal liquido è maggiore che non in acque meno profonde (dato semplicemente dal maggiore o minore peso della quantità di liquido presente, come dice la legge di Stevin), la pressione del liquido vicino ai bordi del contenitore è maggiore di quella al centro, dove il liquido è meno profondo.

Questa differenza di pressione spinge il liquido (e le foglioline di tè) a scorrere dall'esterno verso l'interno, ma a tale flusso si oppone l'azione esattamente contraria della forza centrifuga. Tuttavia, vicino al fondo e ai bordi del contenitore, il movimento del liquido è rallentato dall'attrito con la tazza: la minore velocità in queste parti si traduce in una minore forza centrifuga che non riesce a bilanciare il flusso opposto dovuto alla differenza di pressione.

Si instaura quindi un flusso secondario (quello primario è quello circolare del mulinello generato dal cucchiaino) per cui mentre gira attorno all’asse centrale, il liquido si sposta verso l’esterno in superficie, scende lungo la parete del contenitore, si sposta verso l’interno sul fondo e poi risale lungo l’asse centrale. Questo flusso sul fondo trascina le foglioline di tè che, a causa del loro peso, non riescono a risalire e si depositano al centro. Il tutto viene schematizzato nella figura che segue:

Einstein si occupò di questo fenomeno mentre ne studiava un altro, apparentemente del tutto diverso: l'erosione delle rive dei fiumi causate dallo scorrere dell'acqua.

L'interpretazione del fenomeno delle foglie del tè ha suggerito in tempi recenti lo sviluppo di una tecnologia medica basata su questa segregazione di materiale più pesante verso il centro. Ma, più in generale, il processo può purificare liquidi contenenti materiale più pesante. Insomma, proprio una centrifuga al contrario.

 

Vi piacciono i paradossi? Allora beccatevi anche QUESTO!