Abbiamo da poco affrontato il problema della visione insulsa che hanno certi giornalisti della ricerca scientifica. Ovviamente, ne sfruttano in pieno le realizzazioni pratiche, ma con grande arroganza (e ignoranza, ovviamente) la dileggiano sperando così di minimizzare la loro pochezza intellettuale.

Un problema non certo nuovo nella storia umana che, spesso e volentieri, ha cercato di annullare i progressi della mente al fine di imporre dogmi e credenze posticce, utili per ottenere  potere assoluto e visibilità. Le sfaccettature sono molte, ma tra le tante vi sono quelle relative alla divulgazione delle notizie. Un certo evento di tipo scientifico viene ingoiato da chi ha potere mediatico, elaborato e aggiustato in sintonia con i propri limiti, e poi dato in pasto al popolo comune che, per definizione, DEVE credere in ciò che gli viene regalato.

Purtroppo, i giornali e i media sono saturi di individui di questo genere e la loro proliferazione è enorme. Anzi, con i "social" le persone che credono di poterli imitare crescono a dismisura. Una frase regna spesso sovrana: "Non  capisco  niente di fisica, ma Einstein secondo me ha detto molto idiozie". In poche parole, per bene che vada, ci si convince che solo ciò che si è convinti di saper fare o capire è importante. Purtroppo, sempre più spesso, anche  coloro che potrebbero capire e far capire si adattano alla situazione in cambio di visibilità e notorietà.

Come piccolo esempio voglio raccontarvi ciò che è successo un paio di anni fa in un Liceo Scientifico di Monfalcone. Evento interessante sia per l'argomento in sé, sia per la problematica matematica a cui si riferisce. E' un esempio che mostra come, anche quando si cerca di dare risalto alle capacità di qualcuno, lo si fa -comunque- utilizzando frottole che non possono essere che pericolose per la dilagante ignoranza del popolo medio.

Ecco l'articolo apparso sul Corriere della Sera, il quotidiano più letto (si fa per dire) in Italia:

"Francesco crea al liceo la formula matematica che supera Archimede"

Accidenti, un ragazzino di 16 anni riesce dove non era riuscito nemmeno Archimede. Ben vengano i quotidiani che riescono a scoprire nuovi talenti, supportati dagli stessi insegnanti! Beh... la faccenda non è andata proprio così, a tal punto che quella del giornale può essere considerata una vera bufala, in grado -come sempre- di dimostrare l'ignoranza scientifica di chi l'ha scritta o - al limite- di dare una visione completamente errata della matematica e del mondo che le gira attorno..

Il problema da affrontare è abbastanza "normale" per un sedicenne che ancora non ha affrontato gli integrali:

"Data una parabola e una retta che la intersechi, determinare l'area del segmento parabolico così ottenuto".

Sinteticamente, si tratta della "quadratura della parabola" a cui era giunto Archimede e che dimostrò con il suo geniale metodo meccanico. Dimostrata, poi, anche per esaustione, venne, infine, molti secoli più tardi, risolta mediante l'integrazione. Quest'ultimo è il metodo usato oggi, di grande rapidità e precisione. Resta, comunque, il fatto che la formula ricavata da Archimede è ancora valida e seguita.

La formula dice che l'area del segmento di parabola è uguale ai 4/3 dell'area del triangolo in essa inscritto che ha per base la stessa base (distanza punti di intersezione tra retta e parabola) e per altezza la distanza tra questa retta e quella tangente alla parabola e a lei parallela. Lo vediamo meglio in Fig. 1.

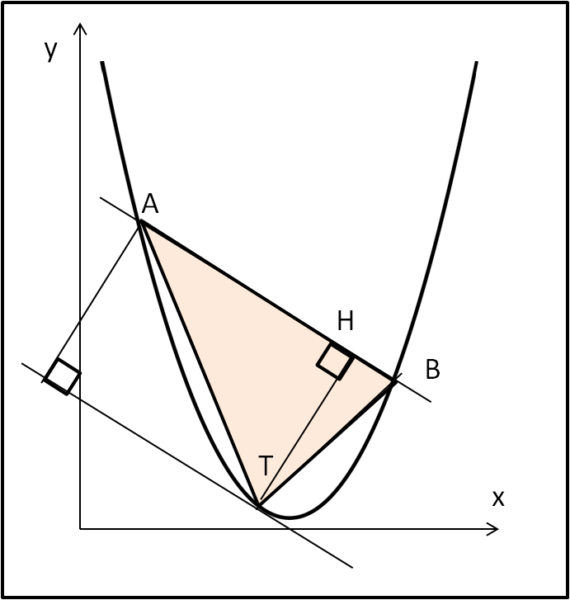
ll problema si limita, perciò, alla determinazione di alcune grandezze geometriche tali da permettere l'applicazione della formula di Archimede. In altre parole, la difficoltà da superare è solo e soltanto quella relativa all'applicazione di una formula ben nota. L'esercizio risulta interessante, dato che abbisogna di vari passi di geometria analitica semplici, capaci di mostrare la preparazione dello studente.

Ovviamente, il primo passo è trovare le intersezioni tra retta e parabola, ossia le coordinate dei punti A e B. Non ci vuole molto e basta fare sistema tra parabola e retta:

y = ax² + bx + c

y = mx + n

Trovate le coordinate dei due punti A(x1,y1) e B(x1.y2), attraverso l'equazione di secondo grado derivante dal sistema, è immediato il calcolo della distanza AB.

Il passo successivo è quello di trovare l'equazione della retta, tangente alla parabola e parallela ad AB. In pratica si ripropone il sistema precedente, dove adesso, però, la retta ha un valore di n variabile (m resta uguale perché la retta deve essere parallela a quella di partenza) e si impone l'esistenza di un solo punto di intersezione, ossia si impone l'uguaglianza a zero del discriminante dell'equazione risolvente. Trovata la retta tangente, ossia n, non resta che calcolare la distanza tra il punto A (ad esempio) e la retta tangente. Questa distanza è l'altezza del triangolo ABT, mentre AB ne è la base. Si può infine applicare la formula di Archimede per la soluzione del problema.

L'esecuzione dei vari passi è indicativa della preparazione dello studente e io la considererei fondamentale.

Se, invece, ci interessa che lo studente sveltisca il più possibile i passaggi algebrici da svolgere e dimostri, in particolare, la sua comprensione dei parametri di retta e parabola realmente necessari, la faccenda può cambiare. In realtà, l'unico parametro della parabola che caratterizza il problema è il coefficiente a, quello del termine di secondo grado, dato che è lui che ne determina la forma. b e c sono solo parametri che ne individuano la posizione nel sistema di riferimento scelto. Richiedendo un'area di segmento parabolico, poco interessa dove la parabola sia posta nel piano, ma solo e soltanto la sua forma. Ne segue che si deve poter trovare una formula che dipenda solo dal coefficiente "a" e dai due punti d'intersezione tra parabola e retta. Questa scorciatoia "pratica" non è difficile da trovare e porta alla formula:

A = 1/6 |a| |(x1 - x2)³|                .... (1) ^(*)

Essa indica chiaramente che l'area dipende dalla retta e dall'apertura della parabola. Resta il fatto che vanno, comunque, calcolate le ascisse dei punti di intersezione. E' possibile fare di meglio? Ossia trovare una formula che, sulla base dei soli coefficienti della parabola e della retta di partenza, ci dia immediatamente la formula da applicare? Sicuramente sì. Questo tipo di approccio è usato normalmente dai matematici (perfino dal sottoscritto) per cecare di "compattare" i vari passaggi da un'equazione all'altra. Lo scopo? Non certo per scoprire nuove formule, ma per limitare possibili errori nella stesura di un programma: meno equazioni si inseriscono e più è facile evitare errori di scrittura, sempre difficili da evidenziare a posteriori.

La strategia da utilizzare è abbastanza semplice: portarsi dietro le varie equazioni scritte in modo più generale possibile e inserire progressivamente, nelle determinazioni  a cui si arriva,  i valori dei parametri ottenuti precedentemente. Più che descrivere il processo a parole, è meglio fare un esempio. Utilizziamo proprio il problema del segmento parabolico.

Iniziamo quindi dalla determinazione dei due punti di intersezione tra retta e parabola generiche. Svolgiamo tutti i calcoli necessari e analizziamo il risultato:

y = ax² + bx + c = 0

y = mx + n

Per risolverla facciamo la differenza tra di loro:

ax2 + (b - m)x + (c - n) = 0

Risolviamo l'equazione:

x1,2 = (- (b-m) +/- √((b - m)² - 4a(c - n)))/2

Il discriminante DEVE essere diverso da zero altrimenti non avremmo una sezione parabolica.

Cosa ci dice la relazione precedente? Che possiamo scrivere facilmente la differenza delle ascisse dei punti di intersezione (in valore assoluto, ovviamente), continuando a utilizzare le equazioni generiche:

Basta scrivere:

|x1 - x2| = | (- (b - m) + √((b - m)² - 4a(c - n))/2a) - ( - (b - m) - √((b - m)² - 4a(c - n))/2a)| =  |2 √((b - m)² - 4a(c - n))/2a |= |√((b - m)² - 4a(c - n))/a|

Cosa abbiamo ottenuto? La differenza tra le ascisse è stata espressa in termini dei coefficienti di partenza della parabola e della retta (a, b, c, m e n).

A questo punto non ci resta che richiamare la formula " (1), che viene data per acquisita, e inserire al suo interno il valore di |x1 - x2| appena ottenuto:

A = 1/6 |a| |(x1 - x2)³| = 1/6 |a| |√(((b - m)² - 4a(c - n))³)/a³| = 1/6 |√(((b - m)² - 4a(c - n))³)|/a²

A = 1/6 |√(((b - m)² - 4a(c - n))³)|/a²

Sì, non è certo una formula banalissima da scrivere in un programma, ma è una e una sola e questa motivazione ne fa preferire la scelta.

Cos'è il risultato ottenuto? Assolutamente niente di straordinario a livello matematico se non quello di utilizzare una sola formula finale che dipende solo dai coefficienti iniziali. Una formula del tutto analoga alla (1) da un punto di vista concettuale, con possibili vantaggi (?) di tipo pratico.

Abbiamo forse superato Archimede? nemmeno per sogno, dato che abbiamo continuato a  usare la sua formula anche se visualizzata in modo diverso. Può avere un certo interesse  per il calcolo effettivo di un segmento parabolico? Direi proprio di no, dato che ormai i "computer" preferiscono gli integrali. C'era, perciò, un vero motivo matematico per dedurla? Sembra proprio di no, se non come esercizio da dare a un ragazzo che non conosce ancora gli integrali. Un problemino molto semplice se lo inseriamo nell'ambito di una qualsiasi prova di un olimpiade matematica... anzi, TROPPO banale.

Avete già capito che l'enfasi data dal nostro giornalista è del tutto gratuita e mostra molto bene come non abbia minimamente capito cosa vuol dire una "scoperta" matematica. Il fatto che evidenzi in modo particolare l'abilità calcistica del giovane studente sembra quasi voler trasmettere un messaggio ben diverso : anche i giocatori di calcio possono essere geni della matematica. In realtà, tra le righe, lo stesso ragazzo ammette la non straordinarietà del risultato, quando dice: "per trovarla (la soluzione)il procedimento era lunghissimo. Così sono partito dall’unico dato noto che avevo, i coefficienti della parabola e della retta, e ho ottenuto il risultato con una formula algebrica". Non parla di "novità", ma di accorciamento di tempi, sempre possibile quando una serie di operazioni può essere condensata in un'unica formula.

Tutto ciò viene, in fondo, confermato dal rettore: "In letteratura la formula non si trova. La si può comunque dedurre da quella più nota con semplici passaggi algebrici".

Ciò che più mi stupisce (sempre che non sia un'altra illazione del giornalista) è la reazione dell'insegnante che non sembra nemmeno di "primo pelo": "Beh, di errori non ce n’erano. Ho verificato io stessa. Dava sempre il risultato corretto. Il primo brivido per la schiena l’ho avuto allora". Addirittura i brividi, quando avrebbe dovuto capire subito il procedimento usato la ragazzo. Anzi, avrebbe dovuto essere lei a proporre quella serie di ovvi passaggi algebrici come esercizio per vedere le capacità intuitive e pratiche dei ragazzi.

Non so cosa dire di più, se non che un'apparente piccola "idiozia" pubblicata dal giornalista potrebbe avere effetti  negativi per la vera comprensione della matematica. In matematica serve capire i concetti non costruire formule da imparare a memoria. Archimede può stare tranquillo... al limite può compiacersi del ragazzo che ha dimostrato di avere capito i passaggi algebrici.

Concludo con un esempio sintetico del valore della nuova "scoperta". E' come se io dovessi usare la relazione (solo usarla!):

y = m t

ma sapessi anche che t può essere legata ad altri parametri secondo un'altra ben nota relazione:

t = s/r2

e "scoprissi" che vale la relazione sconvolgente:

y = m s/r2

No, amici miei, la matematica è ben altra "poesia" e i geni sono ben diversi!

(*) Dimostrazione della formula (1) attraverso gli integrali.

Come già detto, l'area non cambia di certo se trasliamo la parabola e la retta in modo da far coincidere il punto A con l'origine degli assi. Le equazioni diventano:

y = ax² + bx

y = mx

Troviamo il secondo punto d'intersezione tra retta e parabola

ax² + bx = mx

x(ax + b - m) = La soluzione x = 0 corrisponde  al punto A  mentre la soluzione B ha ascissa:

ax + b - m = 0

x = (m - b)/a

Riassumendo:

x1 = 0

x2 = (m - b)/a

x2 = x2 - x1

Abbiamo trovato i limiti di integrazione (0 e x2) e passiamo al calcolo degli integrali. In particolare, calcoliamo quello relativo alla retta a cui togliamo quello relativo alla parabola, in modo da ottenere l'area del segmento di parabola:

A =  ∫₀^x2mx dx - ∫₀^x2(ax² + bx) dx = - ∫₀^x2ax² + ∫₀^x2(m - b)x = - a x2³/3 + (m - b)x2²/2

Ma

(m - b)/a = x2

ossia:

m - b = a x2

Per cui

A = - a x2³/3 + a x2³/2 = a x2³/6 = a (x2 - x1)³/6

che è proprio la (1)