E' un momento in cui la parabola domina il nostro blog... perché non continuare?

Forse sarebbe meglio utilizzare -una volta tanto è permesso-, la definizione inglese: safety parabola che non rimanda a concetti legati alla religione. Anzi, la safety parabola è spesso utilizzata in guerra...

La sua definizione è piuttosto facile: il luogo dei punti dello spazio oltre il quale non si può essere colpiti da un cannone (o cose simili) che spara i suoi proiettili a una certa velocità costante. In realtà può anche essere usata per descrivere il getto dell'acqua quando si scaglia un sasso e problematiche analoghe. In poche parole il punto chiave è che la velocità v_o di espulsione deve essere costante, mentre è libero di variare l'angolo θ che ogni singolo proiettile fa rispetto al piano di terra.

Impostiamo il problema ricorrendo alle ben note equazioni del moto.

Il moto di un proiettile è divisibile in due parti: un moto rettilineo uniforme lungo l'asse orizzontale x e un moto uniformemente accelerato lungo l'asse verticale y, causato dalla forza di gravità terrestre che tende a far cadere il proiettile. In parole matematiche (Fig. 1):

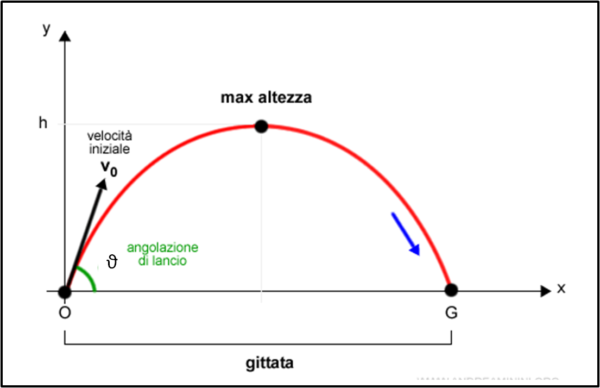
x = v_ocosθ t

y = v_osenθ t - gt²/2

Queste sono equazioni orarie, ossia dipendono dal tempo, mentre noi siamo interessati soltanto alla traiettoria nel piano x,y. Nessun problema... ricaviamo t dalla prima equazione e andiamo a sostituirlo nella seconda, in modo da eliminare il tempo.

t = x/(v_ocosθ)

y = x v_o senθ/(v_ocosθ) - x² g /(2v_o² cos² θ)

y = x tan θ - x² g /(2v_o² cos² θ)               .... (1)

Ovviamente, questa funzione è una parabola che descrive tutte le possibili traiettorie del proiettile al variare dell'angolo θ. Consideriamo adesso un punto P (X,Y) e vediamo quali sono le condizioni per potere essere toccato da una parabola di equazione (1).

Y = X tan θ - X² g /(2v_o² cos² θ)             .... (2)

E' facile ricavare che

1/cos²θ = 1 + tan²θ                   .... (3)

Infatti:

1/cos²θ = (sen²θ + cos²θ)/cos²θ =  sen²θ/cos²θ + cos²θ/cos²θ = tan²θ + 1

Sostituendo la (3) nella (2), otteniamo

Y = X tan θ - X² g (1 + tan²θ)/(2v_o²)

Y = X tan θ - (X² g  +X² g tan²θ)/(2v_o²)

Y = X tan θ - X² g/(2v_o²)  - X² g tan²θ/(2v_o²)

X² g tan²θ/(2v_o²) - X tan θ + (X² g/(2v_o²) + Y) = 0             .... (4)

Questa è un'equazione nella variabile tan θ che può portare a due soluzioni, a una sola o a nessuna a seconda del segno del suo discriminante. Il che vuole anche dire che esistono due parabole che toccano P, una sola o nessuna.

Scriviamo il determinante:

X² - 4 (X²g/2v_o²(X² g/(2v_o²) + Y))

Noi siamo interessati al caso in cui esso è uguale a zero, ossia al caso in cui esista una sola parabola che tocchi P.

X² - 4X⁴g²/4v_o⁴ - 4Y X²g/2v_o² = 0

X² - X⁴g²/v_o⁴ - 2Y X²g/v_o² = 0

2Y X²g/v_o² = X² - X⁴g²/v_o⁴

Y = X²(v₀²/2X²g) - (X⁴g²/ v_o⁴)(v_o²/2X²g)

Y =  - g X²/2v_o² + v_o²/2g                  .... (5)

Essa rappresenta la curva limite per cui i punti esterni non possono essere toccati da nessuna parabola, mentre quelli interni sono toccati da due traiettorie del proiettile. Questa curva limite è quella che si chiama proprio "parabola della salvezza". Essa è, ovviamente e nuovamente, una parabola ed è in pratica l'inviluppo di tutte le possibili traiettorie del proiettile al variare dell'angolo θ, come mostra la Fig. 2.

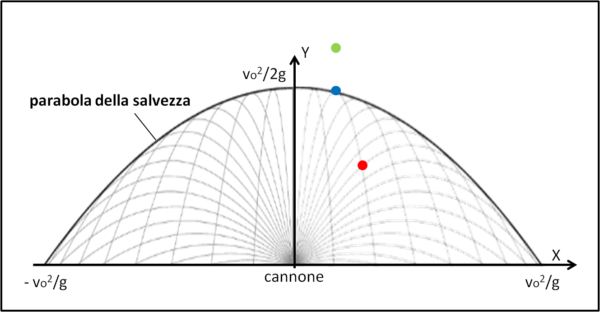
Ovviamente il suo vertice sta nel punto X = 0 e Y = v₀²/2g, mentre interseca l'asse X in due punti: Y = 0 e X_1,2 =+/- v_o²/g. Non ci meravigliamo di certo se il vertice rappresenta il lancio perfettamente verticale, mentre le due intersezioni non sono altro che le gittate massime del cannone.

Nella figura il punto rosso ammette due traiettorie (discriminante maggiore di zero), il punto azzurro ne ammette una sola  e si trova proprio sulla parabola della salvezza (discriminante uguale a zero), il punto verde può vivere tranquillo, dato che nessuna traiettoria può colpirlo (discriminante minore di zero).

Basta ora far ruotare il cannone attorno all'asse y per avere la visione a tre dimensioni (Fig. 2).

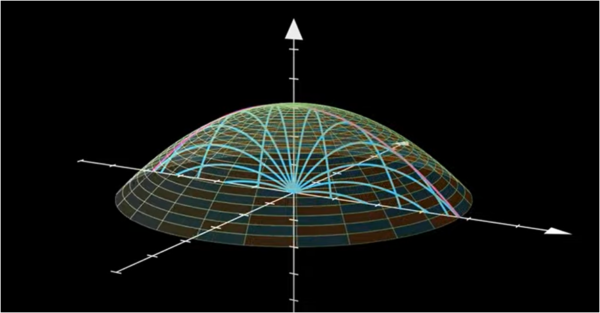
Forse sarebbe meglio chiamarlo "paraboloide di salvezza".

P.S.: Dimenticavo... Chi ha introdotto la parabola di salvezza è stato Evangelista Torricelli.