Categorie: Matematica
Tags: definizione Euclide geometria numeri composti numeri primi prologo
Scritto da: Vincenzo Zappalà
Commenti:5
I numeri primi sono veramente soli. 1. Prologo **
Questo articolo è inserito nella sezione d'archivio "I Numeri Primi"
La matematica sa come definirli, ma non sa ancora come trovarli... Di cosa parliamo? Dei numeri primi, gioia e dolore di tanti grandi matematici attraverso i secoli. Su di essi ci sarebbero da scrivere libri su libri ed è venuta l'ora di farne una breve storia, una storia che non vede ancora un lieto fine.
La loro definizione è semplicissima:
Tutti quei numeri interi positivi, diversi da zero, che possono essere divisi solo per se stessi oppure per uno.
Essi sono tornati alla ribalta del grande pubblico per merito di un romanzo scritto da Paolo Giordano (che in qualche modo faceva riferimento ai numeri primi "gemelli", ossia a quelli separati solo da un numero) e a una conferenza del matematico Odifreddi, che riprendeva il titolo del romanzo, ossia "La Solitudine dei Numeri Primi".
Odifreddi li presenta come numeri solitari, ma prende in considerazione argomenti e proprietà che, a mio modesto parere, sono tutt'altro che chiare e divulgative. Insomma, mi piace poco la sua trattazione.
Preferisco scorgere la loro solitudine attraverso una diversa interpretazione, in qualche modo "umanizzata".
Essi sono SOLI per due motivi tra loro molto stretti: ognuno di loro non ha genitori e, quasi di conseguenza, non può assolutamente procreare. Si sono creati senza l'ausilio di nessuno e, in modo simile, non potranno mai creare un altro come loro. L'azione per poter nascere e procreare è quella che noi chiamo moltiplicazione. Questa, per me, è la vera SOLITUDINE.
In parole più matematiche: Essi possono formare qualsiasi numero intero, ma nessuno con la loro proprietà fondamentale, ossia quella di non avere altri divisori che se stessi (tralasciamo il numero 1 che è divisore di qualsiasi numero e che non viene considerato come numero primo per varie ragioni). D'altra parte se la loro moltiplicazione portasse a un numero primo, questo numero non sarebbe più primo in quanto avrebbe come divisori sia se stesso che la sua radice quadrata. Esempio: 3 è primo, 9 non può essere primo dato che è divisibile sia per se stesso che per 3!
Questa loro caratteristica si ricollega subito al teorema fondamentale della matematica: Qualsiasi numero composto può essere creato solo attraverso il prodotto di numeri primi. In pratica, lo applichiamo normalmente quando eseguiamo la scomposizione in fattori primi, ossia quando cerchiamo in un numero composto i numeri primi che lo hanno formato.
Non ci stupiamo di certo se veniamo a sapere che questo teorema fondamentale è stato introdotto dal solito, immenso, Euclide. Ci stupiamo sempre, invece, pensando che Euclide NON conosceva l'algebra e dimostrava le sue proposizioni attraverso approcci geometrici accomunati a una logica sopraffina.
Vediamo, ad esempio, come lui definiva i numeri primi...
Un numero primo è un numero che può essere misurato solo attraverso l'unità.
Consideriamo un certo segmento la cui lunghezza sia uguale a un numero primo. Ad esempio, consideriamo il numero 7 e il suo segmento corrispondente. Bene. Qual è l'unico segmento che può essere contenuto un esatto numero di volte nel segmento 7? Solo è soltanto il segmento 1, dato che 2 o 3 o 4 o 5 o 6 non ne sono in grado. Ovviamente esiste un altro segmento capace di far ciò... lo stesso numero primo di partenza! (Fig. 1)
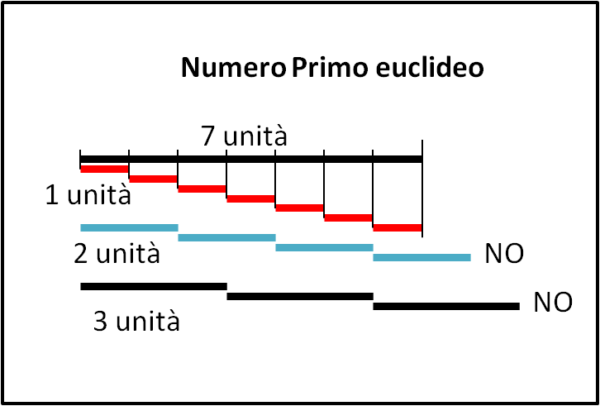
Pochi segmenti ed Euclide ha dato la definizione che ancora oggi viene usata.
Euclide, però, ci "serve" ancora...
Definiti i numeri primi e la loro vera solitudine, riassumiamo tutto ciò che vorremmo sapere su di loro. E' molto facile...
(1) Quanti sono ?
(2) Quali sono ?
(3) Esiste un procedimento capace di trovarli ?
(4) Come si distribuiscono all'interno dei numeri interi positivi ?
Beh... l'unica domanda a cui è stata data una risposta è la prima e la soluzione si deve nuovamente a quel genio prodigioso che è stato Euclide. Tutte le altre aspettano ancora una risposta definitiva...
Forza, cerchiamo di non lasciarli troppo SOLI e facciamo la storia di come gli uomini abbiano provato a rispondere ai loro problemi "psicologici", senza ottenere, però, un vero successo.






5 commenti
Proprio ieri Fabrizio Tamburini ha presentato a Venezia, in anteprima nazionale, il suo nuovo libro "Il mistero dei numeri primi". Tamburini è anche un socio e conferenziere del Planetario del Lido
vuoi dire che è inutile che continui...?
Permalosone! Volevo solo dire che il tema è sempre attualissimo e ben venga un ulteriore tuo intervento in questo affascinante settore :-)
E pensavo che magari tu magari lo conoscessi questo Fabrizio astrofisico, ecc.
Ma io stavo scherzando, scioccone!