(Q) Un bicchiere da riempire ***

04/10/22

(Q) Un bicchiere da riempire ***

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:15

Abbiamo a disposizione un bicchiere cilindrico che ha come base interna una circonferenza di raggio R. La sua altezza interna è  uguale a 2R. Inseriamo 4 sfere di diametro R all'interno del bicchiere in modo che 2 di esse tocchino il fondo e le altre due si appoggino su di loro ortogonalmente, come mostra la figura che segue (in modo da occupare il minimo spazio).

A questo punto, versiamo dell'acqua nel bicchiere fino a che tutte le sfere non siano perfettamente immerse (il livello dell'acqua deve essere tangente alle due sfere superiori).

Si chiede:

Qual è il volume di acqua necessario allo scopo, in funzione di R.

N.B.: invito i nostri "super eroi" ad aspettare un paio di giorni. Per loro è un esercizio sicuramente banale.

QUI la soluzione

Articoli correlati

15 commenti

  1. Cesco
    04/10/2022 at 10:14

    Domanda: le sfere hanno diametro o raggio R/2? Perché la posizione disegnata è per un raggio R/2,ma nel testo c'è scritto diametro

  2. Alberto Salvagno
    04/10/2022 at 12:05

    Il solito errore di stompa del proto. Le sfere ovviamente hanno diametro R e raggio R/2. Ci provo:

    quiz

  3. Vincenzo Zappalà
    04/10/2022 at 19:14

    Sì, avete ragione ho fatto un bel pasticcio... :oops:

  4. Vincenzo Zappalà
    05/10/2022 at 08:42

    N.B.: Dovrei aver messo le cose a posto e resa più chiara la figura. Invito Francesco a riprovare in queste condizioni...

    Scusate ancora...

  5. leandro
    05/10/2022 at 18:58

    Allora, per ragioni di simmetria i centri delle 4 sfere sono vertici di un tetraedro di spigolo =R.
    I 2 segmenti che congiungono i centri delle sfere inferiori e quello delle sfere superiori
    sono spigoli opposti di un tetraedro.
    Ora i centri di 4 spigoli di un tetraedro sono i vertici di un quadrato,
    quindi le sue diagonali sono la distanza di due spigoli opposti.
    Essendo i lati del quadrato la metà degli spigoli (talete applicato a un triangolo equilatero), la distanza tra due spigoli opposti sarà R/2 \sqrt[]{2} .
    Tale distanza deve essere sommata a due raggi delle sfere , cioè R.
    Quindi 3/4 R \sqrt{2} è l'altezza dell'acqua.
    Il calcolo del volume è banale.

  6. leandro
    05/10/2022 at 19:00

    Mi correggo: l'altezza è 3/2 R \sqrt{2}

  7. leandro
    05/10/2022 at 19:05

    E' una serata non favorevole al ragionamento  h= R+ R/\sqrt{2} = R(1+1/\sqrt{2})

  8. Vincenzo Zappalà
    05/10/2022 at 19:10

    Leandro, ti dispiacerebbe scrivere la formula finale? Sarà banale, ma è sempre meglio arrivare fino in fondo...

  9. leandro
    06/10/2022 at 07:46

    beh si, bisogna sottrarre dal volume del cilindro= \pi R^{2} R (1-\frac{1}{\sqrt{2}})

    il volume delle 4 sfere=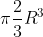 \pi \frac{2}{3}R^{3}

    viene \pi R^{3} (1+\frac{1}{\sqrt{2}}-\frac{2}{3})

     

  11. Vincenzo Zappalà
    06/10/2022 at 08:36

    Occhio, Leandro, alla prima formula che hai scritto...

  12. Andy
    06/10/2022 at 10:56

    Il mio ragionamento è questo:

    unendo i centri delle 2 sfere color sabbia in basso, il segmento congiungente sarà pari a due volte il raggio della sfera, cioè R;

    successivamente, unendo i rispettivi centri delle 2 sfere sabbia in basso con il centro di una delle sfere verdi in alto, si otterranno due distanze entrambe pari ad R;

    morale della favola, si disegna un triangolo equilatero di lato R, ma che giace su un piano non ortogonale al piano sul quale giace la base del bicchiere, bensì inclinato con un certo grado.

    Una figura, guardando il bicchiere dall’alto, visualizza meglio:

     

    Se invece si guarda il bicchiere da una visione laterale, il segmento inclinato è il triangolo equilatero di prima visto di “taglio”, secondo la sua dimensione di misura maggiore (il segmento tratteggiato blu), ovvero l’altezza, che in un triangolo equilatero e pari a lato × √3 / 2

    allora si riesce a vedere un triangolo rettangolo di ipotenusa pari all’altezza del triangolo equilatero e di cateto minore pari al raggio della sfera che è R/2:

    applicando il teorema di Pitagora, si determina la misura del segmento blu tratteggiato incluso tra i due raggi verticali delle sfere, che è anche il cateto maggiore del triangolo rettangolo di cui prima:

    linea \:blu=\sqrt{(\frac{R\sqrt3}{2})^2 - (\frac{R}{2})^2} = \sqrt{\frac{R^2 \:3}{4} - \frac{R^2}{4}} = R \sqrt{\frac{1}{2}} = R \frac{\sqrt2}{2}

     

    allora l'altezza h sarà uguale a: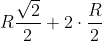 R \frac{\sqrt2}{2} + 2 \cdot \frac{R}{2} = R (\frac{\sqrt2}{2} + 1)

    Non resta che calcolare il volume del cilindro di altezza h e sottrarre 4 volte il volume della sfera di raggio R/2, per ottenere il volume dell'acqua necessaria a ricoprire le sfere sino a quando il pelo dell'acqua è tangente alle sfere poste in alto:

    V = \pi R^2 \: (\frac{\sqrt2}{2} + 1)R - 4 \cdot \frac{4}{3} \pi (\frac{R}{2})^3 = \pi R^3 (\frac{\sqrt2}{2}+1) - \frac{2}{3} \pi R^3

    che semplificata diventa:

    V = \pi R^3 (\frac{\sqrt2}{2} + \frac{1}{3})

     

    P.S.

    Per curiosità, il piano su cui giace il triangolo equilatero è inclinato rispetto al piano della base del bicchiere di:  arccos(\frac{1/2}{\sqrt3 / 2}) ≈ 54°,73561

     

    Sperando che il tutto sia corretto...

     

  13. Andy
    06/10/2022 at 14:49

    Chiedo scusa, errata corrige:

    secondo la descrizione che ho fatto, nella prima immagine ho invertito i colori delle sfere:

    quelle sabbia si trovano di sotto, andamento nord-sud, le verdi sopra andamento est-ovest.

     

  14. leandro
    06/10/2022 at 15:36

    \pi R^{2}R(1+\frac{\sqrt{2}}{2})

    La prima formula che esprime il volume del cilindro a pelo d'acqua.

    Il volume delle sfere è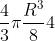 \frac{4}{3}\pi \frac{R^{3}}{8}4

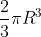
    = \frac{2}{3}\pi R^{3}

    da cui il volume d'acqua = \pi R^{3} (1+\frac{\sqrt{2}}{2}-\frac{2}{3})

    Sembra che i valori concordino con quelli di Andy.

  15. leandro
    06/10/2022 at 15:45

    Qualcuno si chiederà perché esiste un quadrato inscritto nel tetraedro.

    Beh ogni faccia è un trangolo equilatero. se congiungiamo i punti medi di questo triangolo otteniamo un segmento pari a metà spigolo e ad esso parallelo, quindi due triangoli adiacenti hanno segmenti mediani paralleli. Stesso ragionamento per gli altri 2 triangoli equilateri. Per ragioni di simmetria anche gli angoli del quadrilatero sono uguali , quindi si tratta di un quadrato inscritto nel tetraedro. Qui la simmetria gioca un ruolo essenziale.

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.