L'unica vera difficoltà di questo problema geometrico è, forse, quello di riuscire a visualizzare un sistema in tre dimensioni attraverso le sue proiezioni piane. Leandro ha seguito il procedimento che utilizza un tetraedro e sono ben lieto che lo abbia fatto perché probabilmente è il metodo più elegante. Io, invece, esporrò un metodo che sfrutta al meglio le visioni piane del sistema, in modo simile a quanto fatto da Andy. Complimenti, ovviamente, sia a Leando che ad Andy.

Consideriamo da prima la visione dall'alto come mostra la Fig. 1

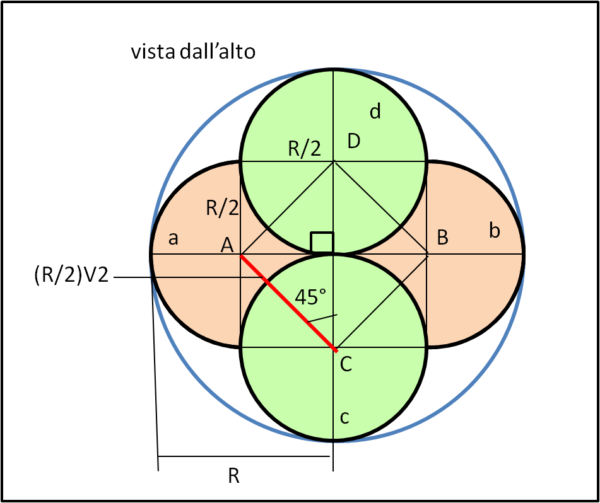
Le due sfere rosa si sistemano nel piano inferiore e le due sfere verdi nel piano superiore. Le congiungenti i loro centri formano tra loro un angolo di 90°. Con Pitagora segue immediatamente che:

AC = R√2/2

Adesso, ruotiamo il nostro bicchiere come mostra la Fig. 2, guardandolo sempre dall'alto:

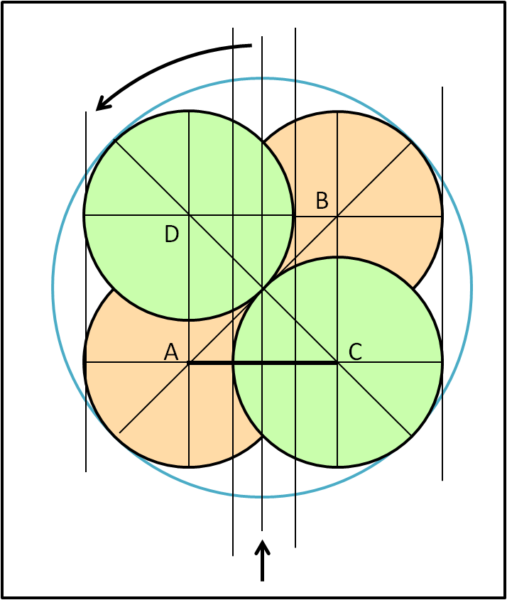
Non ci resta che rappresentare la visione laterale, come vista dalla direzione della freccia nera:

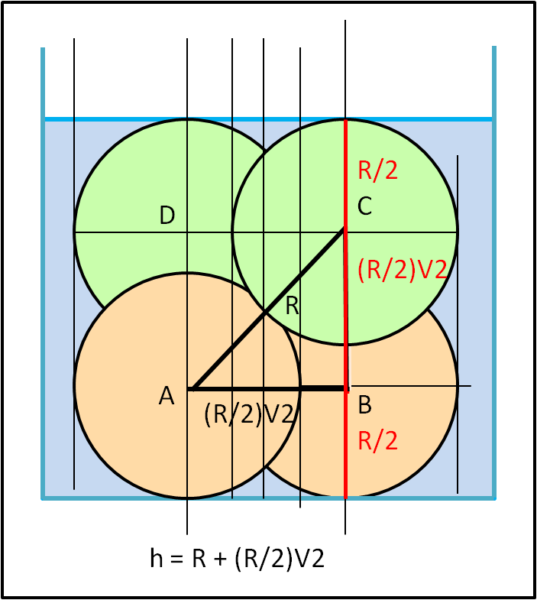
Avendo cambiato la visione, quello che prima avevamo segnato come segmento AC, diventa, adesso, il segmento AB. La distanza tra i centri della sfera rosa e verde non è altri che R. Ne segue che anche BC deve essere uguale ad AB, sempre per Pitagora.

L'altezza dell'acqua h tale da coprire interamente le 4 sfere, è perciò:

h = R/2 + R/2 + R√2/2 = R(1 + √2/2)

Calcoliamo il volume del cilindro pieno d'acqua:

Vc = π R² h = π R³(1 + √2/2)

Calcoliamo il volume delle 4 sfere:

Vs = 4 (4/3 π (R/2)³) = π R³(16/24) = π R³ 2/3

Non ci resta che togliere dal volume del cilindro pieno d'acqua il volume delle quattro sfere per ottenere il volume dell'acqua necessaria a coprire completamente le sfere.

Va = Vc - Vs = π R³(1 + √2/2) - π R³ 2/3 = π R³(1 + √2/2 - 2/3) = π R³(1/3 + √2/2)

Va = π R³(2 + 3√2)/6

QUI trovate il quiz.