Questo articolo è inserito in Matematica e Geometria

 

Il punto: la più piccola entità geometrica.

Piccola sì, ma importantissima! Talmente importante che il matematico svizzero Jakob Steiner nel 1826 introdusse la definizione di potenza di un punto, attraverso un teorema che può essere scritto come segue:

Consideriamo un cerchio di centro O e un punto P (esterno o interno al cerchio). Tracciamo da P una retta qualsiasi che intersechi il cerchio in due punti. Il prodotto delle lunghezze da P ai due punti di intersezione è una costante. Questa costante viene chiamata POTENZA del punto P.

N.B.: Il teorema si estende anche a un punto P preso sulla circonferenza.

Questa semplice definizione si basa, come quasi tutta la geometria "normale", su teoremi enunciati dall'immenso Euclide (non per niente si chiama euclidea). Le sue applicazioni sono molteplici e permettono di risolvere problemi geometrici di grande interesse.

Prima di cominciare, permettetemi di fare uno strano confronto. Aver definito il potere di un punto rispetto a un cerchio è un po' come aver descritto una semplificazione geometrica della legge di gravitazione universale o, addirittura, della relatività generale. Esse, infatti, ci dicono che la presenza di una certa massa influenza un qualsiasi punto che si trovi a una certa distanza (teoricamente, anche interno ad essa). Se identifichiamo la massa con un cerchio di un certo raggio, il potere di un punto ci dice proprio quali sono gli effetti della massa-cerchio su di esso, compreso il caso in cui il punto sia proprio sulla circonferenza (qualcosa come il raggio di Schwarzschild per i buchi neri?).

Scusate l'assurda divagazione e torniamo al teorema.

Per la dimostrazione basta richiamare due teoremi di Euclide, quello delle corde e quello delle secanti, che, in fondo, sono la stessa cosa. Mentre il primo è ben conosciuto, il secondo è molto meno pubblicizzato... Enunciamoli e dimostriamoli rapidamente attraverso una geometria veramente elementare.

 

Il teorema delle corde

Da un punto P qualsiasi interno al cerchio  tracciamo due corde qualsiasi che intersechino la circonferenza in A, B e C, D. (Fig. 1).

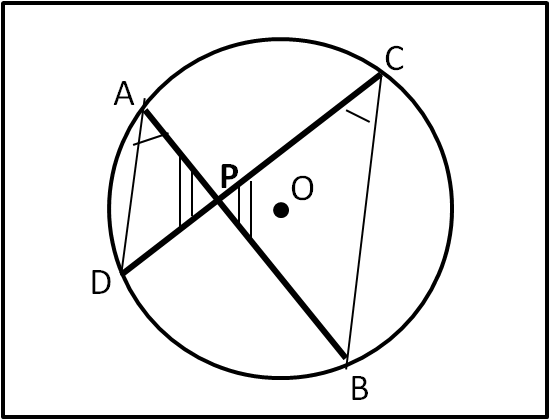
Il teorema dice che vale la relazione:

PA · PB = PC · PD

La dimostrazione è immediata e basta tracciare i segmenti AD e CB. I due triangoli APD e CPB sono simili in quanto gli angoli APD e CPB sono uguali, mentre DAB = DCB perché angoli alla circonferenza dello stesso arco DB. Dalla similitudine segue che:

PA/PD = PC/PB

e, di conseguenza anche la tesi.

Il fatto che angoli alla circonferenza di uno stesso arco siano uguali è conosciuto da tutti, ma -forse- non tutti conoscono un suo caso particolare. Consideriamo in Fig. 2 un arco AB e facciamo variare il punto P lungo la parte di circonferenza maggiore tra A e B.

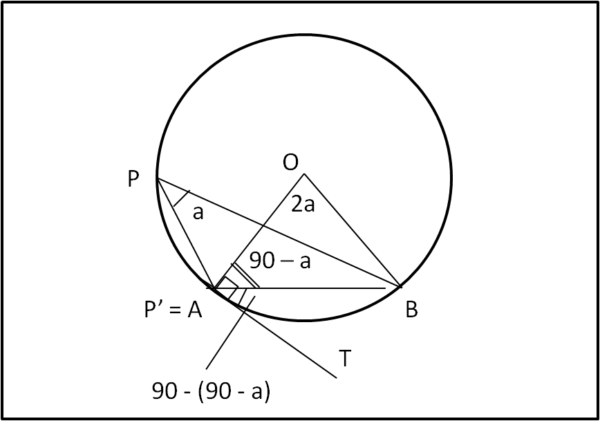
L'angolo acuto APB = a è sempre uguale a stesso. Se facciamo variare P lungo l'arco minore della circonferenza otteniamo un angolo ottuso che è sempre uguale a stesso ed è supplementare a quello precedente.

(a) Cosa succede, però, se il punto P viene a coincidere con A (o con B)? L'angolo acuto che rimane uguale a se stesso è in questo caso l'angolo tra la congiungente A con B e la tangente alla circonferenza nei punti A (o B). Dimostriamolo...

Uniamo O con A e B. Il triangolo OAB è isoscele (OA = OB) e, quindi, OAB = OBA. Sappiamo che AOB è doppio dell’angolo alla circonferenza APB = a. Ne segue che OAB =  (180° – 2a)/2 = 90° – a.

AT è la tangente alla circonferenza in A e, quindi, OAT = 90°. Ne segue che TP’B = TAB = 90° – (90° – a) = a, come volevasi dimostrare.

Teniamo da conto questo risultato che ci servirà tra non molto...

 

Teorema delle secanti

Questa volta consideriamo il punto P esterno al cerchio e da esso tracciamo due rette che intersechino la circonferenza rispettivamente in A, B e C, D. Dobbiamo dimostrare che vale sempre la relazione precedente, ossia:

PA · PB = PC · PD

Consideriamo la Fig. 3

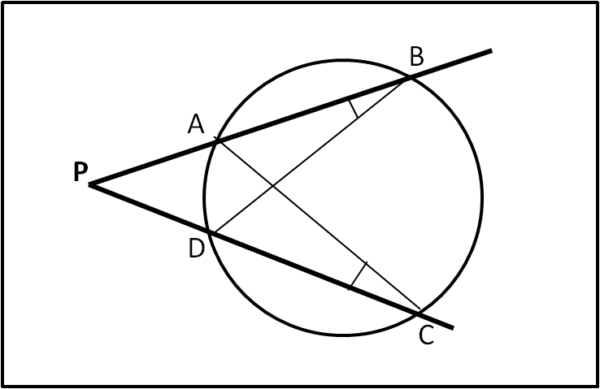
I due triangoli PAC e PDB sono simili in quanto l'angolo in P è in comune e gli angoli in B e C sono uguali perché entrambi angoli alla circonferenza di uno stesso arco AD.

Ne segue che

PA/PD = PC/PB

e, quindi, la tesi:

PA · PB = PC · PD

Ci rimane da dimostrare il teorema della secante e della tangente, relativo al caso particolare in cui una delle due rette sia tangente alla circonferenza nel punto T (Fig. 4).

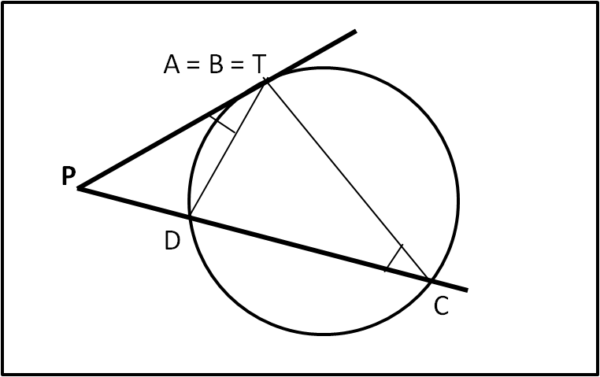
In questo caso consideriamo i triangoli PTD e PTC. Essi hanno l'angolo in P in comune e gli angoli PTD e TCD uguali in quanto entrambi angoli alla circonferenza dello stesso arco DT. Questa uguaglianza la possiamo confermare per quanto dimostrato precedentemente in (a).

Ne segue che:

PD/PT = PT/PC

e, di conseguenza:

PT² = PD · PC

Che è esattamente il teorema della secante, nel caso in cui A coincide con B e con T.

 

Potenza di un punto

Uniamo P con il centro O del cerchio (Fig. 5).

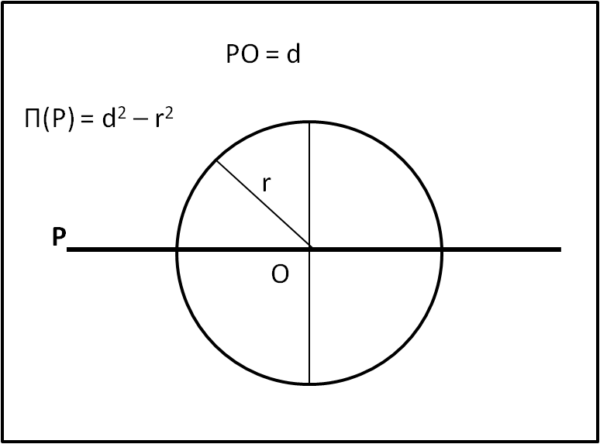
Definiamo la potenza Π(P) del punto P rispetto alla circonferenza di raggio r e centro O nel seguente modo:

Π(P) = d² - r²

dove d è la distanza di P dal centro O.

Ma cosa c'entra questa definizione con il nostro teorema iniziale? C'entra eccome! Dopo aver dimostrato i teoremi di Euclide, possiamo tranquillamente dimostrare il teorema della potenza. Basta un attimo di riflessione e la Fig. 6:

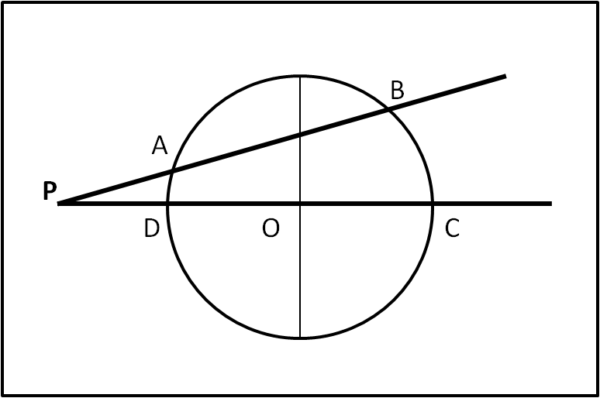
Se vale il teorema delle secanti, è ovvio che come retta tracciata da P, posso prendere proprio quella che passa per il centro O. Ne segue che per qualsiasi altra retta secante vale la relazione:

PA · PB = PD · PC

Ma

PD = d - r

e

PC = d + r

Sostituendo:

PA · PB = (d - r)(d + r) = d2 - r2 = Π(P)

e il teorema iniziale è dimostrato. In altre parole, basta tracciare una secante al cerchio e moltiplicare tra loro le distanze dal punto P alle intersezioni con la circonferenza per ottenere la potenza del punto P rispetto al cerchio.

Si può anche fare di più, conoscendo il teorema della tangente-secante. Al posto del prodotto PA · PB si può scrivere PT², dove T è il punto di tangenza. Ne segue che il quadrato della distanza tra P e il punto di tangenza T ci regala nuovamente la potenza del punto. Quest'ultima definizione deriva facilmente anche da una semplice applicazione del teorema di Pitagora, come mostra la Fig. 7.

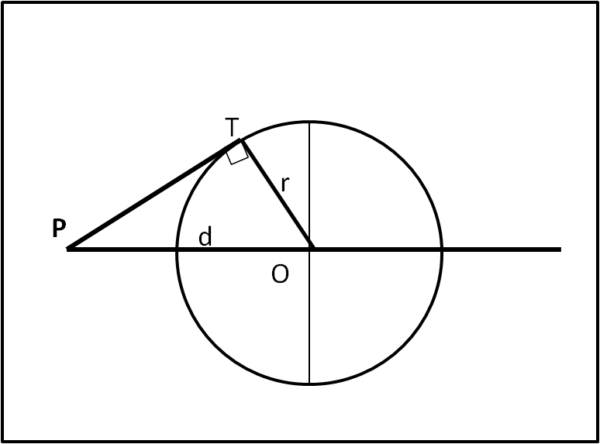
Uniamo O con T e consideriamo il triangolo rettangolo PTO. Per Pitagora abbiamo:

PT² = PO² - OT² = d² - r² = Π(P)

Concludiamo notando immediatamente che la potenza di un punto è:

• positiva se il punto è esterno al cerchio
• negativa se il punto è interno
• uguale a zero se il punto sta sulla circonferenza

La potenza di un punto si può estendere facilmente nelle tre dimensioni e permette "capriole" geometriche non banali.

 

QUI un'applicazione del teorema della tangente-secante