Categorie: Matematica
Tags: Archimede esaustione rettificazione circonferenza spirale velocità
Scritto da: Vincenzo Zappalà
Commenti:13
Rettificazione della circonferenza **
Questo articolo vuole rispondere a una precisa richiesta del nostro amico Pierluigi riguardante la dimostrazione che ha permesso ad Archimede di rettificare una circonferenza, ossia di trovare un segmento che abbia la stessa lunghezza dell'intera circonferenza. In questo contesto, l'articolo può essere considerato come completamento di questa trattazione. Un risultato eccezionale che, però, ricordiamo non risolve il problema della quadratura del cerchio con riga e compasso, dato che fa uso di una curva che opera come "macchina" per ottenere lo scopo.
La dimostrazione di Archimede, per quanto è giunto fino a noi, sembra che fosse ottenuta attraverso il solito metodo dell'esaustione. Un procedimento lungo e che nasconde la parte più essenziale: "Perché mai Archimede avrebbe dovuto pensare alla spirale e a quel particolare segmento?" Probabilmente, perché aveva già capito a cosa poteva andare a parare. Lasciatemi, allora, risolvere la rettificazione della circonferenza con un metodo che non comporta derivate o trigonometria, ma solo un preciso ragionamento e un paio di triangoli simili.
Il metodo era stato esposto da Torricelli e Roberval nel XVII secolo e io ho cercato di renderlo il più intuitivo possibile, cercando di mettermi nei panni del grande matematico (Dio mi perdoni!).
Iniziamo, allora, la nostra dimostrazione partendo proprio dalla lontana, ossia dalla spirale dello stesso Archimede, la macchina giusta per il giusto scopo. Che tipo di moto descrive un punto che disegna la spirale? Un moto composto da due moti uniformi, uno di traslazione lungo la retta (il bastone) che ruota e uno dovuto proprio alla rotazione del bastone. Introduciamo la Fig. 1.
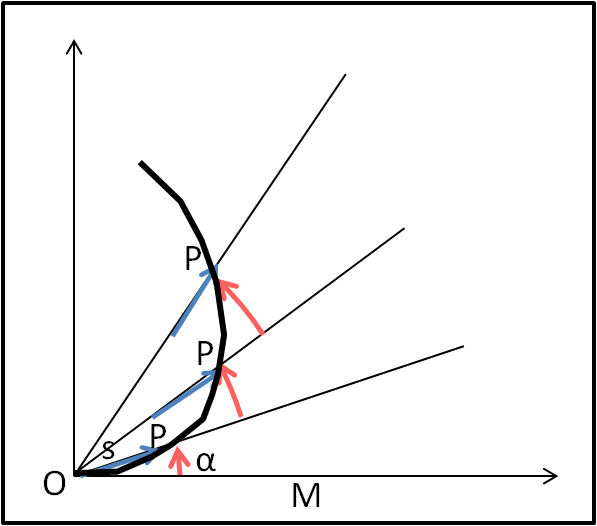
Descrivendo un moto siffatto, il punto P parte dall'origine ed è soggetto ad una velocità lungo l'asse rotante e ad una velocità angolare propria del bastone. Entrambe le velocità sono costanti e possono essere scritte come:
vr = s/t
dove s = OP(t)
ω = α/t
dove α = MOP
In tempi uguali il punto P si muove sulla spirale spostandosi di un segmento s lungo il bastone e ruotando di un angolo α.
Al tempo t qualsiasi il punto P continua a essere soggetto alle due velocità costanti vr e ω.
Descriviamo la nostra circonferenza da rettificare, avente raggio R = OP (Fig. 2)
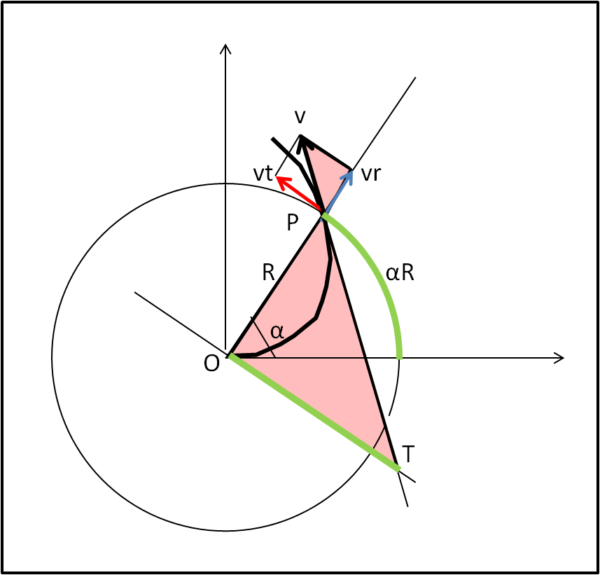
Nel punto P la tangente alla spirale individua la direzione della velocità v che è la combinazione di vr e ω. Possiamo facilmente scrivere che:
vr = R/t
ω R = vt (vt velocità tangenziale nel moto circolare uniforme)
Ma sappiamo anche che:
ω = α/t
vt = αR/t
vr e vt sono le due componenti in cui si può scomporre la velocità v del punto P che descrive la spirale.
Adesso, tracciamo la perpendicolare da O alla congiungente OP e prolunghiamo la tangente alla spirale in P fino a incontrare la perpendicolare in T.
I due triangoli rosa sono simili per costruzione, per cui possiamo scrivere la proporzione:
OT/OP = vt/vr = (αR/t)/(R/t)= Rαt/Rt = α
OT/OP = OT/R = α
OT = Rα
Ma Rα non è altri che l'arco di cerchio che corrisponde all'angolo α. Per cui il segmento OT ha una lunghezza pari all'arco di circonferenza di raggio R. La nostra circonferenza è stata rettificata.
Il caso generale della figura, infatti, può essere riportato al caso particolare in cui α = π/2.
Otteniamo la Fig. 3
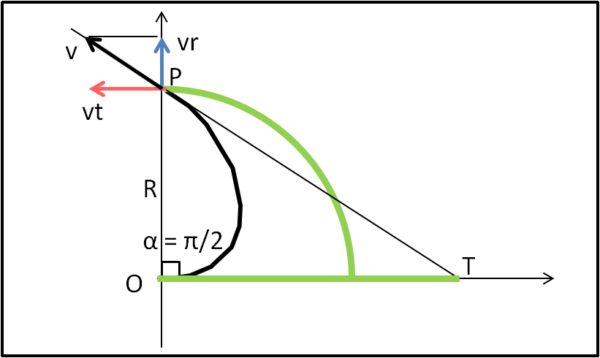
Essa ci dice che il segmento OT è uguale all'arco di cerchio della circonferenza di raggio R, corrispondente ad un angolo di π/2. Ne segue che 1/4 di circonferenza è uguale ad OT. Basta tracciare un segmento OT pari a quattro volte quello indicato in figura per avere la lunghezza dell'intera circonferenza!
Molti contestano che questo metodo possa essere stato pensato da Archimede per due motivi:
(1) Archimede conosceva la scomposizione di un vettore?
(2) Perché Archimede dice di avere usato l'esaustione?
Mi permetto di rispondere in modo molto personale:
(1) Scomporre il modulo di una velocità secondo due direzioni tra loro perpendicolari segue, in fondo, direttamente dal teorema di Pitagora.
(2) Probabilmente l'esaustione lo vedeva come protagonista ed era considerato un metodo molto "alla moda".
Ovviamente, posso aver torto, ma sono convinto che Archimede fosse in grado di affrontare il problema secondo quanto descritto. In ogni caso, ho dato una risposta a Pierluigi senza usare derivate e trigonometria, ma solo semplice geometria.
Spero di averlo accontentato...






13 commenti
Grazie, una prima osservazione: nella figura 3 parli del segmento AT ma la lettera A non c'è. Ti riferisci forse invece ad OT?
ovviamente sì, caro Pierluigi... correzione fatta e grazie!
Una prima osservazione: la Spirale di Archimede permette di ottenere un segmento che è un quarto di circonferenza. Anche la Quadratrice di Dinostrato produce un segmento lungo un quarto di circonferenza. Possiamo quindi dire che le 2 curve hanno stessa lunghezza?
Non per niente entrambe vengono usate per la trisezione dell'angolo e la rettificazione della circonferenza. Due curve ugualmente adatte allo scopo. In fondo abbiamo sempre la combinazione di un moto traslatorio e uno circolare, entrambi uniformi... Ma questo fatto non dice che le curve hanno la stessa lunghezza, bensì che servono entrambe a misurare una stessa lunghezza.
Che calcolo si può usare per determinare la lunghezza della Spirale di Archimede?
Dall'equazione della curva si calcola l'integrale di linea... ma mi sembra di andare troppo nel particolare. La formula, comunque, si trova facilmente
L =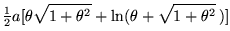
dove a è il passo
Sì, è un aspetto molto specifico della questione che servirebbe a confrontare la lunghezza della Quadratrice di Dinostrato con quella della Spirale di Archimede.
Tornando invece al discorso generale, come si può arrivare alla stessa dimostrazione usando la Trigonometria?
Non so Pierluigi, prova a cercare tu se trovi qualcosa a riguardo...
L'ho chiesto perché alla fine dell'articolo hai scritto che la dimostrazione si basa sulla geometria senza ricorrere a trigonometria o derivate. Ho effettuato una ricerca per la trigonometria, ma senza esito. Usando invece le derivate si arriverebbe allo stesso risultato?
Ma a quale dimostrazione ti riferisci? Si sta facendo confusione...
Se ti riferisci alla rettificazione della circonferenza... non vedo perché complicarsi le cose, quando è appena stata dimostrata in modo semplice. Non è cosa banale, ma appena ho un po' di tempo posso anche descriverla. Tuttavia, il blog deve occuparsi di molte cose e non può continuare a battere su una cosa già dimostrata.
Dico bene che la tangente al punto P incontra l’asse x in T? In tal caso PT sarebbe l’ipotenusa del triangolo rettangolo e mediante il Teorema di Pitagora si potrebbe fare la riprova di calcolare OT.
Questa volta, caro Pierluigi, ti accontento ancora, ma poi non posso passare il tempo dietro alla spirale di Archimede. OK?