Torniamo ancora una volta sulla spirale di Archimede e vediamo come si può riuscire a dimostrare l'uguaglianza tra OA e l'arco di cerchio R α, dimostrata vettorialmente (e molto semplicemente) nell'articolo precedente, attraverso la trigonometria e con l'aiuto di un paio di derivate. Pubblico questo metodo per far contento il nostro Pierluigi, ma poi, prometto, che non ci tornerò più sopra.

Iniziamo col ricavare l'equazione polare della spirale e utilizziamo la Fig. 1

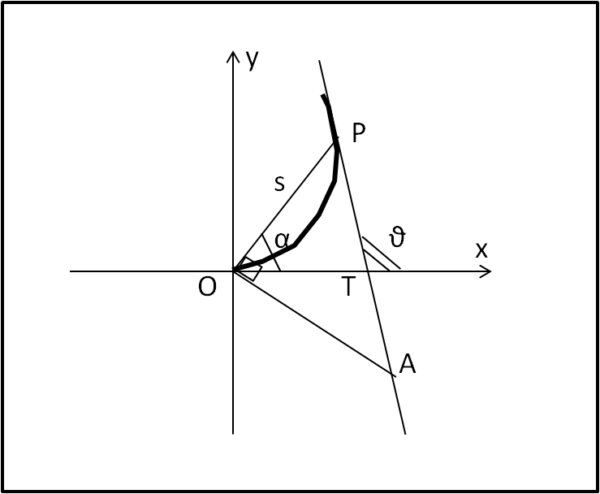
Sappiamo che il punto P che descrive la spirale si muove di moto rettilineo uniforme su un asse, ossia:

s = v t

t = s/v

Nel contempo l'asse ruota di un angolo α e, quindi, P ruota insieme all'asse di una velocità angolare

α = ω t

t = α/ω

in  conclusione, eliminando t:

α/ω = s/v

s = α v/ω

Possiamo scrivere il moto di P in  coordinate polari:

x = s cos α

y = s sin α

Ossia:

x = α (v/ω) cos α 

y = α (v/ω) sin α

A questo punto divertiamoci a calcolare la tangente alla curva nel punto P. Essa deve avere come coefficiente angolare la derivata dy/dx che non è altro che la tangente trigonometrica dell'angolo che la retta fa con l'asse delle x. Chiamiamo questo angolo θ.

dx/dα = (v/ω) cos - α (v/ω) sin α

dy/dα =  (v/ω) sin α + α (v/ω) cos α

dy/dx = ((v/ω) sin α + α (v/ω) cos α)/((v/ω) cos α - α (v/ω) sin α)

tan θ = (sin α + α cos α)/(cos α - α sin α)        .... (1)

Consideriamo il triangolo OPT = OPA

Abbiamo:

θ = π - π + α + OPA

OPA = θ - α

per cui

tan (OPA) = tan (θ - α)

La formula della tangente della differenza di due angoli ci dice che:

tan (OPA) = (tan θ - tan α)/(1 + tan θ · tanα )

Sostituendo tan θ con la (1), si ha:

tan (OPA) = ((sin α + α cos α)/(cos α - α sin α) - tan α)/(1 +(sin α + α cos α)/(cos α - α sin α) · tanα )

Lascio a voi il divertimento di elaborare la formula e giungere al risultato

tan (OPA) = α                      .... (2)

Perché è così importante avere ottenuto questo risultato?

Disegniamo la Fig. 2

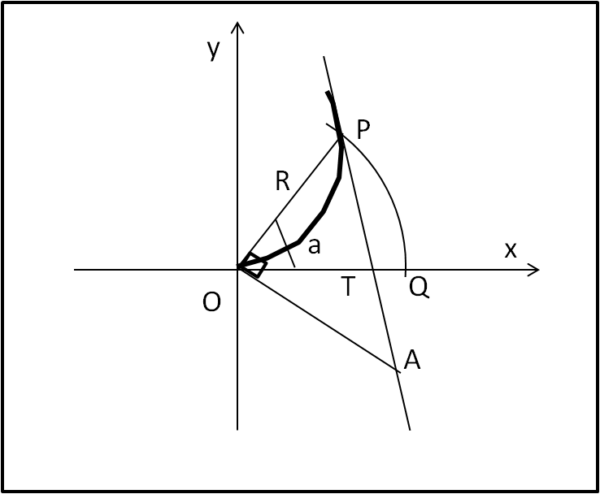
Abbiamo:

arco(PQ) = R α

Vogliamo dimostrare che

OA = R α                                 .... (3)

Ma, vale anche :

tan (OPA) = OA/OP

OA = OP tan (OPA)

OA = R tan (OPA)                .... (4)

Ne segue che dimostrare che OA = R α  vuole dire dimostrare che:

α = tan (OPA)

Ma questo è proprio ciò che è stato dimostrato dalla (2)

Spero che a questo punto Pierluigi sia contento e che ci permetta di ... cambiare argomento (sto scherzando, ovviamente!)