Categorie: Fisica classica
Tags: attrito attrito statico equilibrio inerzia reazione vincolare
Scritto da: Vincenzo Zappalà
Commenti:11
L'attrito: un nemico o un amico? **
QUI gli altri articoli dedicati all'attrito
E' un periodo in cui la matematica e la geometria stanno dominando la scena dl nostro Circolo. Direi di allentare un po' la pressione (anche i numeri primi possono aspettare) e dedicarci un po' alla fisica classica, anche quella più semplice. C'è rischio, infatti, che a volte ci si spinga troppo oltre rispetto a una conoscenza di base, favorendo i più preparati. Questo Circolo vorrebbe accontentare tutti coloro che hanno ancora voglia di far faticare un po' il cervello, e non rivolgersi solo ad una "elite". Introduciamo, allora , un concetto fisico che si cerca sempre di tralasciare e che ha invece un'importanza fondamentale nella realtà di tutti i giorni: l'attrito.
Quante volte, nel cercare di descrivere un fenomeno fisico, abbiamo aggiunto la frase: "Supponendo che non ci sia attrito"? Moltissime volte sicuramente! Questo fatto potrebbe farci pensare che l'attrito sia qualcosa di negativo, che vorremmo eliminare dalla nostra vita quotidiana. Ma è proprio così? Provate a camminare con delle scarpe a suola molto liscia sul ghiaccio o a mettere in moto la vostra automobile su una superficie molto bagnata. In entrambi i casi non vi augurerei di subirne gli effetti. Senza attrito scivolereste sia voi che la vostra macchina!
Eh sì, cari amici, se non ci fosse l'attrito la vita sarebbe molto pericolosa. E, quindi, evviva l'attrito! Quanto ho detto sembra un controsenso e sarebbe giusto chiedersi: "L'attrito è cosa utile o solo un rompiscatole?". La risposta migliore è accettarlo come dato di fatto e utilizzarlo quando è positivo, cercando di escluderlo solo per semplificare la soluzione di un certo problema fisico. Aggiungere l'attrito può essere un ulteriore difficoltà nel cercare di descrivere il moto di un corpo, ma risulta essenziale perché si possano effettuare gran parte dei movimenti che avvengono nella realtà.
E' venuta l'ora di prenderlo in considerazione e capire bene come e perché funziona. Oltretutto, la sua definizione è estremamente semplice e intuitiva. Ben più complicate sono invece le cause che lo generano, dato che per capirle si è costretti a entrare nel microcosmo e tenere in conto le interazioni che avvengono tra le particelle fondamentali della materia. Per adesso, perciò, limitiamoci a descrivere come agisce.
In generale, potremmo dire che l'attrito è una forza che si oppone al moto di un oggetto. Fermandoci qui, potremmo dire che stiamo parlando di inerzia, ossia della prima e della seconda legge di Newton. La prima ci dice infatti che un corpo qualsiasi, non soggetto a nessuna forza esterna, mantiene il suo stato di moto rettilineo uniforme che può anche essere nullo, quando il corpo è fermo. La seconda legge, però, ci dice anche che se volessimo mettere in moto un corpo fermo dovremmo impartirgli una forza capace di donargli un'accelerazione. Se la forza è di brevissima durata, il corpo continuerebbe a muoversi di moto rettilineo uniformo governato dalla sua massa costante: a parità di forza, l'accelerazione sarebbe più o meno grande solo in base alla massa che deve essere spostata. In poche parole, possiamo confermare che questa costante tipica del corpo è un qualcosa che si oppone al moto. Tuttavia, per piccola che sia la forza, ne deve seguire, in qualsiasi caso, un movimento, per piccolo che sia. Ribadiamo ancora che, se la forza viene cancellata, il corpo continua a muoversi con la velocità acquisita grazie all'accelerazione impartitagli.
Quanto detto, però, capita nel vuoto... e il vuoto è un qualcosa ben lontana dalla nostra vita quotidiana. Se imprimessimo una forza a un oggetto sul pavimento, esso potrebbe anche non muoversi affatto o, più facilmente, si muoverebbe con un'accelerazione molto più bassa di quanto detto da Newton e non continuerebbe a muoversi di moto rettilineo uniforme, ma tenderebbe a rallentare fino a fermarsi. Un fenomeno analogo accadrebbe se facessi rotolare qualcosa sul pavimento, ma anche se lanciassi qualcosa attraverso l'aria, a parte la gravità che tenderebbe a farla cadere.
Dobbiamo, perciò, concludere che, oltre alla massa inerziale, deve esistere qualcos'altro che si oppone al movimento dell'oggetto. Questo "qualcosa" è una forza che nasce dal contatto tra due oggetti, di cui uno può essere, ad esempio, il pavimento. Questa forza è chiamata attrito.
Si possono avere tre tipi di attrito: radente, volvente e viscoso. Il primo si ha quando si ha uno strisciamento tra due corpi, il secondo quando si ha un rotolamento, il terzo quando il movimento avviene all'interno di un fluido. Iniziamo a parlare di attrito radente, forse il più semplice da trattare.
L'attrito radente, può essere di due tipi: statico o dinamico. La differenza sta nello stato di moto del corpo. Si ha il primo quando si ha un corpo fermo rispetto a un altro e si vuole iniziare a farlo muovere, si ha il secondo quando il corpo è già in movimento relativo e si vuole variare il suo moto.
Bene, iniziamo con l'attrito radente statico.
Consideriamo un certo oggetto A posto su una superficie B. Essi sono relativamente fermi. Quali forze agiscono sul corpo A? Beh... se siamo sulla Terra agisce sicuramente la forza di gravità Fp che tende a far cadere A verso il basso. Ma se è posto sul pavimento (che diventa la superficie B), il corpo A subisce anche una forza di reazione Rp da parte di B che è uguale e contraria alla forza peso. Una forza questa che non implica alcun movimento, essendo perpendicolare alla superficie su cui il corpo può scivolare. Tuttavia, è proprio questa reazione, che possiamo anche chiamare vincolo, che, alla fine, causa l'opposizione al movimento del corpo in direzione ad essa perpendicolare. Non solo massa, allora, ma anche reazione vincolare.
Detto in parole molto povere, per adesso almeno, la reazione mette a contatto la superficie di A e la superficie B, causando un'interazione più o meno profonda tra di esse, soprattutto a livello microscopico. E' ciò che viene anche chiamata rugosità o irregolarità di superficie e dipende chiaramente dal tipo di materiale e da quanto esso abbia subito una maggiore o minore levigatura. Una scarpa sul terreno fa fatica a scivolare se il terreno è pieno di irregolarità, ma può portare a gravi ruzzoloni se il terreno è, ad esempio, formato da ghiaccio.
Possiamo perciò dedurre che la forza che si oppone al movimento di strisciamento tra due superfici, dipende dalla reazione vincolare e dal tipo di superfici che la reazione mette a contatto. La reazione agisce in direzione perpendicolare al pavimento, ossia alla superficie B su cui si vuole far scorrere il corpo A, mentre, invece, la forza che si oppone allo scorrimento, ossia la forza d'attrito, agisce sul piano di scorrimento, in direzione uguale a quella della forza che vogliamo impartire per smuovere l'oggetto A, ma in verso opposto. Non basta, però, dato che questo vettore-forza deve essere moltiplicato per un certo fattore adimensionato μs che si lega al tipo di materiale e al suo grado di levigatura, ossia alla reciproca scorrevolezza. Un fattore che varia tra zero, quando non vi è assolutamente attrito (caso teorico di Newton), e un valore massimo di 1.
Normalmente, la forza di reazione vincolare è uguale a contraria alla forza peso del corpo che si vuole mettere in moto, ma può essere anche maggiore se si imprimesse una forza supplementare al corpo schiacciandolo, ad esempio, verso il pavimento. La forza di reazione è sempre perpendicolare al piano di scorrimento, per cui ciò che conta è la componente della forza peso (e di qualsiasi altra forza si applichi sul corpo) normale alla superficie.
Notiamo, infine, che mentre la reazione vincolare non si oppone direttamente al movimento, la forza d'attrito è una forza "latente" sul corpo A, che agisce solo quando gli imponiamo una forza F che tende a farlo muovere e, in particolare, scorrere lungo B. Si ha movimento solo se
F > μs Rp
La figura che segue riassume schematicamente quanto detto finora:

Il coefficiente μs è un valore tipico per i legami chimici e fisici che esistono tra i due corpi a contatto e ci dice, in pratica, quale forza dobbiamo imprimere per poter muovere il corpo A. Se è zero basta una qualsiasi leggerissima forza; se è uguale a 1 la forza deve essere pari, in modulo, alla reazione vincolare. In casi particolari può addirittura superare 1. E' facile trovare sulla rete le tabelle con i più importanti coefficienti di attrito.
Per adesso, fermiamoci, qui e vediamo di presentare un paio di problemi pratici e di svolgerli strizzando l'occhio alle condizioni di equilibrio statico. Li presenterò come quiz, dando però la soluzione: chi se la sente potrà sempre risolvere da solo il problema e poi controllare il risultato.






11 commenti
Chiedo un piccolo chiarimento, forse sottointeso nell'articolo. Il valore di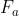 non dovrebbe essere comunque minore del valore di F?
non dovrebbe essere comunque minore del valore di F?
Con , il modello sopra farebbe muovere A indietro. Questo farebbe pensare che
, il modello sopra farebbe muovere A indietro. Questo farebbe pensare che 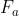 del nostro modello dipenda anche da F, almeno come limite superiore.
del nostro modello dipenda anche da F, almeno come limite superiore.
Cerco di spiegarmi meglio. Supponiamo di fare diverse tentativi di spostare A da fermo con forze decrescenti fino a che non riesco più a muoverlo, vale a dire fino a che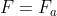 . Se riduco ulteriormente la forza applicata F e
. Se riduco ulteriormente la forza applicata F e 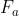 dipendesse solo da
dipendesse solo da 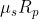 , il modello sopra ci direbbe che A inizia a muoversi all'indietro.
, il modello sopra ci direbbe che A inizia a muoversi all'indietro.
caro Fabrizio,
l'attrito nasce solo quando si applica una forza. Secondo la tua ipotesi, se io non applicassi forza l'oggetto dovrebbe muoversi comunque. Ma questo è assurdo. Fa non può causare moto, può solo contrastarlo.
Fabrizio, capisco bene il tuo dubbio, ma lo chiarisce bene la frase di Vincenzo:
Notiamo, infine, che mentre la reazione vincolare non si oppone direttamente al movimento, la forza d'attrito è una forza "latente" sul corpo A, che agisce solo quando gli imponiamo una forza F che tende a farlo muovere e, in particolare, scorrere lungo B. Si ha movimento solo se F > μs Rp
Si ha movimento solo se F > μs Rp
Pensiamo a un muro... Se io spingo posso anche subire una forza di reazione, ma il muro non si muove. Nel caso in esame c'interessano solo le forze applicate al muro. Se aumento la forza, però, a un certo punto il muro si rompe. Il muro non può superare una certa resistenza. Così l'attrito non supera un certo valore.
Mettiamola così. Se io lancio un pietra contro l'oggetto A, la pietra subisce una forza uguale e contraria. Può anche tornare indietro o rompersi a causa della reazione. Tuttavia, A non si muove perché l'attrito lo tiene fermo. Per farlo muovere devo superare proprio questa forza che è propria del corpo A e che compare solo se si cerca di rompere l'equilibrio statico. Ricordiamo che il corpo A è vincolato al pavimento ed è in quiete proprio grazie alla reazione alla forza peso. La stessa forza peso, però, potrebbe vincere sulla reazione che mantiene l'equilibrio: il pavimento si rompe e A si muove verso il basso. Fino a un certo peso il pavimento si oppone come vincolo, ma se la forza peso aumenta, si ottiene la rottura dell'equilibrio. Tuttavia, se diminuisco la forza peso, il corpo non si muove verso l'alto, ma resta in quiete: la reazione "si adegua". In questo caso si parla di resistenza del materiale del pavimento... ma il discorso è analogo.
Mi è chiaro quanto dite e corrisponde alla esperienza. Però il mio commento non è su questo, ma semplicemente sul modello di questa della forza d'attrito. Se il modello descritto nell'articolo prevede che:
1) l'attrito nasce in presenza di una forza F che tenta di mettere in movimento A;
2) l'intensità della forza che si contrappone al movimento è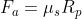 , (che appare indipendente dalla intensità di F).
, (che appare indipendente dalla intensità di F).
Allora, secondo il modello, cosa accade se applico una forza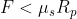 ?
?
Per il punto 1) nasce l'attrito che si contrappone al movimento poichè c'è la forza F. Infatti ci aspettiamo che A non si muova.
Meno chiara è l'applicazione del punto 2) del modello. Se, secondo il modello, l'intensità della forza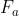 è
è 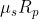 , allora la risultante delle forza applicate su A è
, allora la risultante delle forza applicate su A è 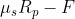 , che ha una intensità
, che ha una intensità 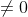 invece di essere nulla. Vale a dire che l'applicazione delle leggi di Newton (che comunque valgono anche in presenza di attrito se consideriamo anche le forze che lo rappresentano) porterebbe a contraddirre l'affermazione ricordata da Alberto "Si ha movimento solo se F > μs Rp"
invece di essere nulla. Vale a dire che l'applicazione delle leggi di Newton (che comunque valgono anche in presenza di attrito se consideriamo anche le forze che lo rappresentano) porterebbe a contraddirre l'affermazione ricordata da Alberto "Si ha movimento solo se F > μs Rp"
Per questo mi aspetterei che il modello di questa forza di attrito preveda che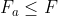 . Ad esempio
. Ad esempio
che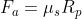 per
per  e
e  per
per 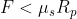 .
.
In questo modo il modello della forza d'attrito rappresenterebbe anche l'affermazione "Si ha movimento solo se F > μs Rp".
Forse ho capito il tuo problema... Penso che tutto vada a posto se consideriamo come forza di attrito il suo valore massimo affinché A si muova. Se la forza che impartiamo è minore è anche minore la forza di attrito e riesce a pareggiare i conti, mantenendo l'equilibrio. Per iniziare il movimento è necessario che la forza di attrito raggiunga il suo valore massimo. Resta comunque il fatto che la forza d'attrito massima è quello che è e dipende solo dalla reazione della forza peso (in modulo), moltiplicata per il valore del coefficiente di attrito tipico del materiale. E' un po' come se la forza d'attrito non si sprecasse inutilmente e finché può si limitasse a essere uguale e contraria alla forza che impartiamo noi. Possiamo scrivere:
0 ≤ Fa ≤ Fa max
D'accordo?
Aggiungo:
la forza d'attrito Fa reagisce alla forza F che impartiamo noi. Questa reazione è sempre uguale e contraria alla forza F, ma ha un suo valore massimo, che dipende dal coefficiente e dalla reazione alla forza peso. Se F supera questo valore, il corpo si muove. Pensiamo che stiamo lavorando sui corpi solidi e non su punti.
D'accordo su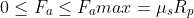 ,
,
Volendolo inserire in un programma dovrei scrivelo
per dare dei valori definiti a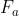 .
.
Per quanto può valere la mia opinione, mi pare corretto