Per non cadere la nostra scala deve restare in equilibrio. Perché questo sia ottenuto sono necessarie due condizioni (Equazioni Cardinali della Statica):

(1) La somma delle forze deve essere uguale a zero

(2) La somma dei momenti delle forze rispetto a un punto qualsiasi deve essere uguale a zero

In poche parole, forze e momenti devono annullarsi.

Consideriamo dapprima la nostra scala di lunghezza L, soltanto appoggiata al pavimento, come mostra la Fig. 1.

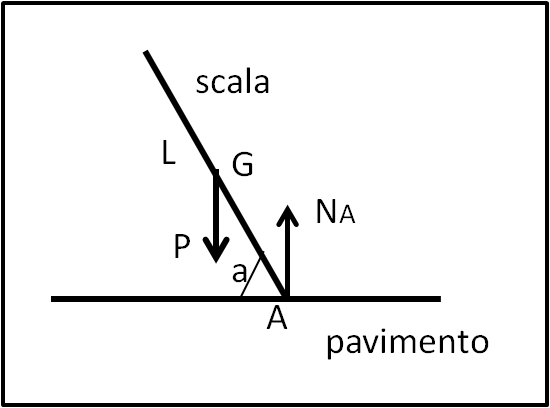
Essa subisce la reazione vincolare N_A in A, perpendicolare al pavimento e parallela alla forza peso P, che possiamo applicare nel baricentro della scala. Non vi sono altre forze. Utilizziamo le Equazioni Cardinali.

(1) Le forze sono due, parallele e con verso contrario. Ne segue che i loro moduli devono essere uguali:

N_A = P

(2) Calcoliamo la somma dei momenti rispetto al punto A. Vi è un solo momento, ossia quello della forza P, dato che quello di N_A vale zero in quanto passa per il punto A (il braccio della forza è zero).

Ne segue che non possiamo avere equilibrio, dato che il momento di P non si può annullare. La conseguenza è che la scala ruota attorno ad A finché non cade tutta sul pavimento.

Per fermare la scala nella sua rotazione proviamo a inserire un  muro che blocchi la rotazione. Il punto B sia il punto d'incontro tra scala e muro. Adesso le forze che agiscono sulla scala sono tre: la forza peso e le due reazioni vincolari N_A e N_B, in A e B (Fig. 2)

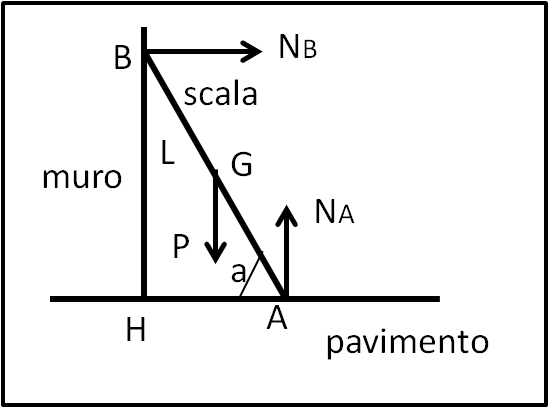
(1) Annulliamo i momenti, che adesso sono due (quello di N_B e quello della forza peso), sempre rispetto ad A.

Il braccio di N_B non è altri che L  (lunghezza della scala) per il seno di a. Il momento è, quindi:

M1 = N_B L sin a

Il braccio di P non è altri che L/2 per il coseno di a, ossia P L/2 cos a, dato che il baricentro si trova a una distanza da A pari a L/2.

M2 = P L/2 cos a

I due momenti hanno segno contrario e quindi possiamo eguagliare i moduli:

N_B L sin a = P L/2 cos a

N_B = P/(2 tan a)

(2) Annulliamo le forze.

Iniziamo da quelle verticali, che hanno verso opposto.

N_A = P

Accidenti! Abbiamo ancora una forza(N_B) che rimane da sola e non si può annullare.

Conclusione: potremmo anche fermare la rotazione della scala, ma non potremmo vietare che il vincolo in B "sposti" tutta la scala verso destra. Facendo ciò si perde il vincolo in B e la scala ruota come abbiamo visto nel primo caso. In modo molto semplicistico potremmo dire che la scala scende e si sposta verso destra permettendo una rotazione che, appena bloccata, costringe la scala a spostarsi ancora un po' e via dicendo fino a che non si adagia sul pavimento. In altre parole, la scala è sempre in moto, un moto roto-traslatorio, descritto rigorosamente da Fabrizio.

Assodato che senza attriti la scala cade sempre, vediamo di esercitarci distruggendo (teoricamente) la Relatività Generale.

Non perdetevi il prossimo quiz!