Una scala semplificata (new, con appendice)**

13/11/22

Una scala semplificata (new, con appendice)**

Categorie: Fisica classica Tags: Scritto da: Vincenzo Zappalà Commenti:4

QUI gli altri articoli dedicati all'attrito

 

Semplifichiamo il problema della scala e vediamo di riuscire ad arrivare a una soluzione concorde...

Per far ciò eliminiamo l'attrito della scala contro il muro. La situazione è quella di Fig. 1

Figura 1

Annulliamo le forze, ottenendo:

FA = NB

P = NA

Vogliamo metterci nelle condizioni di massimo attrito possibile, ossia scriviamo:

FA = μ NA

Ne segue che:

NB = FA = μ NA = μ P

Annulliamo i momenti rispetto ad A

NB L sin a = P x cos a

Sappiamo, però, che NB = μ P, quindi:

μ P L sin a = P x cos a

μ L sin a = x cos a

x = μ L tan a                      .... (1)

x = 0.35 . 5 . 1.73 = 3.03

L'imbianchino può salire di meno...

Dove sta il punto critico di questa soluzione? Indicatemi per bene quale relazione non è corretta...

APPENDICE

Sembra che ciò che dà più fastidio sia il coefficiente di attrito massimo...

Bene, allora prendiamo la relazione:

NB L sin a = P x cos a

e scriviamo, al posto di NB, FA  (obbligatorio per l'equilibrio)

L'equazione ci dice quando vi è equilibrio, su questo non si discute.

FA L sina a = P x cos a

Ricaviamo FA

FA = P (x/L tan a)

Tutta la parentesi è una costante per l'imbianchino che sale a una certa altezza. Segue che:

FA = k P

e k è proprio il coefficiente massimo per ottenere l'equilibrio.

Se

FA < (x/(L tan a) P

se x/L decresce può anche diminuire a.

La Natura impone un certo valore per l'equilibrio.

Articoli correlati

4 commenti

  1. Cesco
    13/11/2022 at 15:30

    Eliminando l'attrito sul muro togliamo una forza diretta verso l'alto che aiuta a tenere la scala in piedi.

  2. leandro
    13/11/2022 at 18:30

    Questa rappresentazione grafica rende tutto più semplice

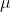    La tangente dell angolo \beta rappresenta sempre il coefficiente \mu, indipendentemente dalla

    posizione della scala; questo per effetto della imposizione di staticità.

    P = Na + Fb

    E' interessante notare che al variare di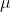 \mu il punto si muove su una circonferenza di raggio P/2 ; quando \alpha è massimo \beta sarà minimo e viceversa

    Dalla figura si calcola subito Nb = P/2 (cos 2\alpha)  , indipendentemente da tutto il resto. Idem per Na .

     

    .....

  3. Fabrizio
    14/11/2022 at 01:16

    Se c'è un punto critico, io non lo vedo.

    Le 3 equazioni della statica,  N_{B} - F_{A} = 0\; , \; \; N_{A} - P = 0\; , \; \; x P \cos{\left(\alpha \right)} - L N_{B} \sin{\left(\alpha \right)}= 0, danno un'unica soluzione per ciascun valore di x:

    N_{A} = P \qquad N_{B} = \dfrac{x P}{L \tan{\left(\alpha \right)}} \qquad F_{A} = \dfrac{x P}{L \tan{\left(\alpha \right)}} .

    Le soluzione sono di equilibrio se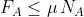 F_A\le\mu\, N_A. Sostituendo le forze con le espressioni trovate diventa:

    \frac{ x P }{L \tan{\left(\alpha \right)}} \leq \mu P.    Quindi è possibile l'equilibrio per  x \leq \mu {P \! \! \! \! {\color{Red} \backslash}}\frac{L \tan{\left(\alpha \right)}}{P \! \! \! \! {\color{Red} \backslash}}=0.35\,5 \tan(60^o)=3,03.

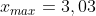    Da cui x_{max}=3,03.

  4. Vincenzo Zappalà
    14/11/2022 at 08:16

    va beh... in qualche modo abbiamo risolto il problema. Cambiamo argomento...

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.