QUI gli altri articoli dedicati all'attrito

 

Un breve riassunto sull'attrito radente insieme ad un'applicazione classica.

Abbiamo parlato molto di attrito, facendo un esempio che ha portato a lunghe discussioni. Temo che questo fatto abbia confuso un po' le idee a riguardo. Riprendiamo, allora, l'argomento dall'inizio e applichiamolo poi a un corpo inserito su un piano inclinato. Penso che quest'esempio sia decisamente più semplice e intuitivo.

Poggiamo il nostro corpo rigido su un piano (pavimento) orizzontale e cerchiamo di farlo scorrere (Fig. 1).

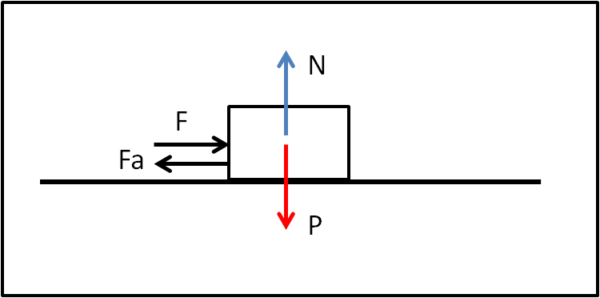
Se non vengono applicate forze esterne, il corpo rigido è soggetto solo a due forze: la forza peso P e la reazione vincolare N del pavimento. In queste condizioni il corpo è in equilibrio e non subisce nessun attrito. Vale ovviamente la relazione

N = P

Il nostro scopo, però, è quello di muovere il corpo verso destra. Introduciamo, allora, una forza F diretta verso destra. Il contatto tra il corpo rigido e il pavimento cerca di opporsi al movimento e lo fa attraverso una forza di attrito Fa. Questa forza riesce a opporsi alla forza F fino a un certo valore di quest'ultima. Ossia, aumentando la forza, aumenta anche la forza di attrito che riesce a mantenere l'equilibrio del corpo. Vi è, però, un limite a tutto ciò e, se la forza supera la forza di attrito massima (che dipende sia dalla forza peso P, ossia dalla reazione N che è uguale e contraria, sia da un certo coefficiente tipico delle superfici a contatto), il corpo inizia a muoversi verso destra. In queste condizioni critiche possiamo scrivere che la forza impressa al corpo uguaglia la forza di attrito massima:

F = Fa^max = μ_sN

Questa fase, in cui la forza aumenta fino a riuscire a superare anche l'attrito massimo è quella che abbiamo visto nella Fig. 1 di quest'articolo. In particolare ricordiamo la linea inclinata a 45°, in cui all'aumentare della forza impressa F aumenta la forza d'attrito Fa, che riesce a uguagliare la forza F. Se questa, però, va oltre un certo limite, la forza d'attrito è costretta a cedere e il corpo si muove verso destra. Entriamo nella fase di attrito dinamico in cui si ha un coefficiente μ_d che è normalmente minore di μ_s. L'attrito dinamico rimane costante e deve subire la forza che viene impressa al corpo. Se questa rimane costante il corpo si muove con velocità uniforme, altrimenti accelera o rallenta. Ciò che è importante notare è che l'attrito statico si adegua alla forza che si imprime (fino a un certo valore limite), quello dinamico è invece una costante.

Limitiamoci a un caso emblematico di equilibrio statico e dinamico, quello di un corpo rigido posto su un piano inclinato, illustrato in Fig. 2.

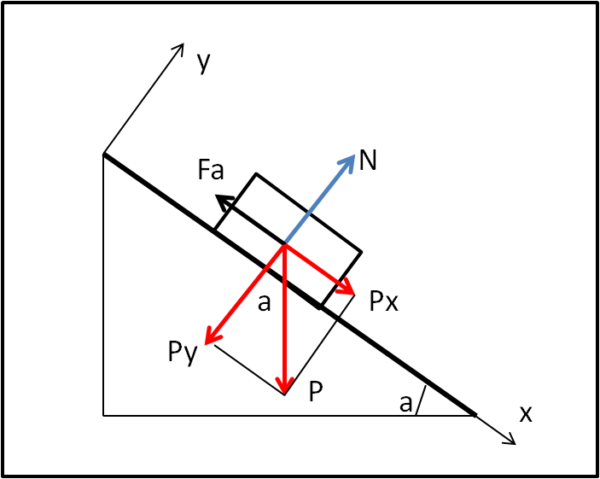
Il corpo ha peso P e l'inclinazione del piano è pari ad a. Disegniamo tutte le forze in gioco. Sul corpo rigido oltre che la forza peso è applicata la reazione vincolare N che è diretta in direzione perpendicolare al piano di appoggio. Agisce inoltre la forza d'attrito lungo il piano d'appoggio e diretta verso sinistra (si oppone allo scorrimento verso il basso). Introduciamo due assi (x,y) ortogonali tra loro, in cui quello delle ascisse è lungo il piano di scorrimento e quello y perpendicolare ad esso.

Scomponiamo la forza peso P nelle sue due componenti. la componente Py è quella che agisce verso il piano inclinato e causa la reazione vincolare N uguale e contraria. Non vi sono altre forze lungo l'asse y, per cui la risultante delle forze è sempre pari a zero:

Py = N

il corpo ha quindi un'accelerazione ZERO lungo l'asse y, qualsiasi siano i valori dell'attrito, dell'angolo a e del peso P.

Passiamo all'asse delle x. Sono presenti due forze: la componente Px della forza peso diretta verso il basso e la forza d'attrito Fa, diretta in verso opposto. Ricordiamo ancora che per fare iniziare a muovere il corpo verso il basso è necessario che la componete della forza peso superi la forza di attrito massima.

La componente della forza peso Px, che tende a far muovere il corpo verso il basso, è data da:

Px = P sin a

Per mantenere il corpo fermo, la forza d'attrito deve uguagliare (in modulo) questa componente

Riesce, però, a far ciò,  solo fino al suo valore massimo che è:

Fa^max = μ_sN cos a = μ_sP cos a

Si mantiene, perciò, l'equilibrio statico fino a che:

P sin a = μ_sP cos a

Ossia:

tan a = μ_s

Come previsto le vere incognite sono due, il coefficiente d'attrito e l'angolo a. Conoscendone una, si ricava l'altro nelle condizioni limite per l'equilibrio statico.

Notiamo, inoltre, che la forza peso P sparisce (più aumenta il peso e più aumenta la reazione vincolare e quindi l'attrito), ma è lei che con la sua componente y aiuta l'attrito a equilibrare, finché può, la forza impressa al corpo, che è però donata, anch'essa, dalla forza peso, mediante la sua coordinata lungo x. La forza peso ha un ruolo sia di agitatore che di calmante...

Notiamo, inoltre, che in queste condizioni limite anche l'accelerazione lungo l'asse x è ZERO, ossia il corpo non si muove.

Immaginiamo, adesso, che l'angolo a, ad esempio, sia molto grande, ossia superi l'angolo limite per far restare il corpo in equilibrio statico (tan a >μ_s) . In questo caso, la componente Px supera la forza d'attrito massima e il corpo è costretto a scivolare verso il basso. Calcoliamo la sua accelerazione:

m a_x = P sin a - Fa^max cos a > 0

m a_x = mg sin a - Fa^max cos a > 0

Ho lasciato indicata Fa dato che a questo punto dobbiamo introdurre l'attrito dinamico e vedere cosa succede, ricordando che Fa_d = μ_dP = μ_dmg = costante

a_x = g(sin a - μ_d cos a)

Il corpo è soggetto a un'accelerazione positiva se è positiva la quantità entro parentesi, ossia se

a_x = sin a - μ_d cos a > 0

Ciò capita se

μ_d cos a < sin a

tan a > μ_d

L'accelerazione è invece negativa, ossia il corpo rallenta, se

μ cos a > sin a

ossia

tan a < μ_d

il corpo, infine, si muove con accelerazione uguale a ZERO, ossia di moto rettilineo uniforme, se:

tan a = μ_d

Normalmente, quindi, se il corpo si muove senza forze aggiuntive, ma solo a causa dell'angolo critico a , la tan a continuerà, a maggior ragione, a essere maggiore di μ_d < μ_s.