Abbandoniamo il quiz sulla quadratura del cerchio, ma colleghiamo il problema a un genio assoluto di arte e di scienza.
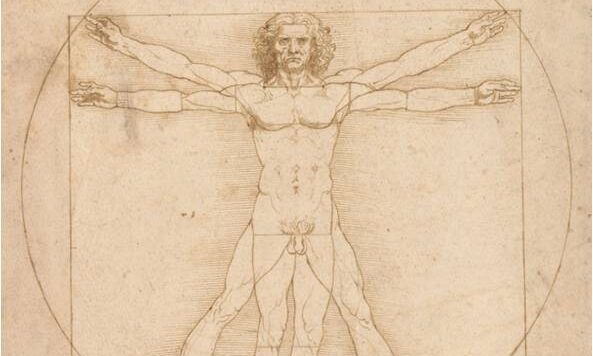

Abbandoniamo il quiz sulla quadratura del cerchio, ma colleghiamo il problema a un genio assoluto di arte e di scienza.

L'homo sapiens sapiens è costretto a riscrivere il cielo stellato per aiutare lo sviluppo dei cellulari, l'organismo artificiale più importante per le future generazioni.
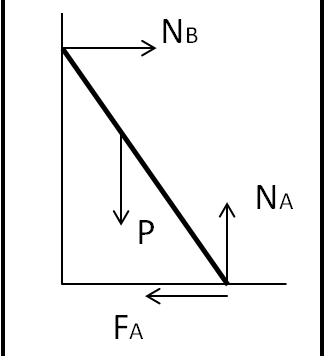
Riprendiamo ancora la nostra scala e semplifichiamo il problema. Forse così sarà più facile trovare il nocciolo del disaccordo o dell'equivoco che sia...

Un imbianchino esperto di statica avrebbe, forse, non fatto mai nascere la relatività generale...
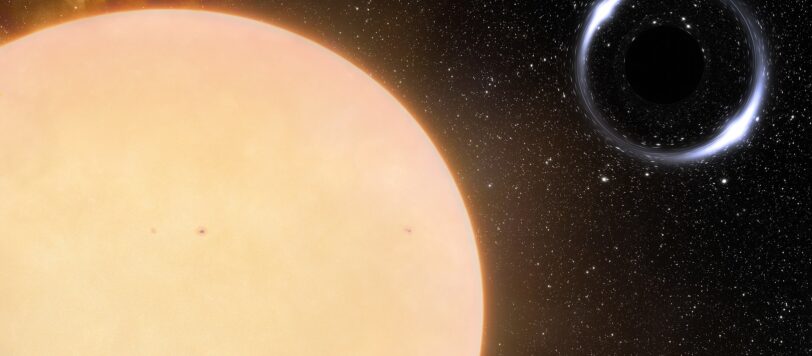
Scoperto il buco nero più vicino a noi, anche se cercava di mimetizzarsi evitando di... mangiare.
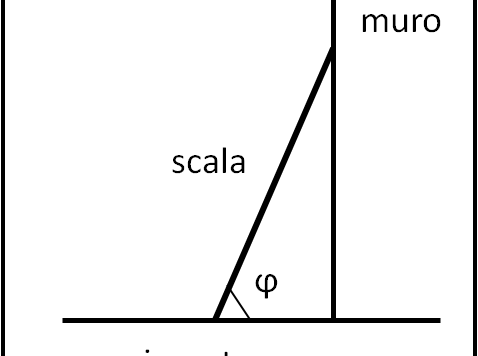
Abbiamo introdotto l'attrito statico radente e siamo pronti a vederne un paio di applicazioni. Tuttavia, prima di iniziare, vi pongo una domanda che sembra banalissima (e forse lo è), a cui, però, viene normalmente risposto senza alcuna spiegazione fisica.
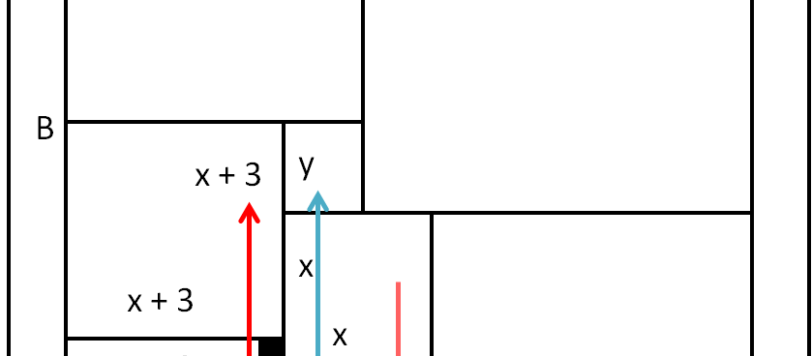
Un quiz che è, forse, risultato un più difficile del previsto. Bravo, come sempre, al nostro Fabrizio.

Il cielo viene osservato di notte... ma la luce diurna potrebbe nascondere qualcosa di molto pericoloso.
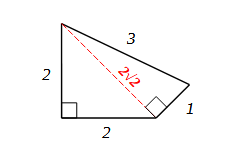
Questo articolo nasce come una serie di considerazioni e prove numeriche “sul campo” relative al teorema di Pitagora e all’ipotesi di Enzo su di una sua estensione a qualsiasi poligono, che ha ottenuto un primo riscontro particolare grazie alla “riscoperta” della spirale di Teodoro di Cirene. L’ipotesi di Enzo era quella di vedere, se possibile, l’applicabilità del teorema di Pitagora anche a poligoni con più di tre lati. Così ho deciso di tentare algebricamente se fosse stato possibile trovare una identità di tipo pitagorico (inizialmente limitata solo per valori interi) per poligoni generici con più di tre lati.