Iniziamo con le derivate delle funzioni trigonometriche che ci permetteranno di fare entrare in scena il primo dei limiti notevoli fondamentali.

Funzione seno

f(x) = sin(x)

Credete che sia una faccenda semplice? Assolutamente no e ci presenta proprio un bellissimo gatto che si morde la coda.

Facciamo finta di non sapere cosa succederà e proviamo  a eseguire il rapporto incrementale della funzione seno e passare al limite per h che tende a zero.

d(sin x)/dx = lim_{h →0} (sin (x + h) - sin (x))/h = lim_{h →0} ((sin x cos h + cos x sin h) - sin (x))/h

d(sin x)/dx = lim_{h →0} ((sin x cos h)/h + (cos x sin h)/h - sin (x))/h)

Il limite di una somma è uguale alla somma dei limiti e sin x e cos x sono costanti rispetto ad h, che è la nostra variabile:

d(sin x)/dx =lim_h→0 sin(x)(cos h - 1)/h + lim_h→0 cos x sin h/h

d(sin x)/dx = sin x  lim_{h →0} (cos h -1)/h + cos x  lim_h→0sin h/h          .... (1)

Ahi, ahi... il limite segnato in grassetto si pone subito come un ostacolo imprevisto. Sostituendo  h con 0 cadiamo in una forma indeterminata 0/0. Un bel problema che, però, abbiamo imparato a trattare attraverso la regola De L'Hôpital, ossia facendo la derivata del numeratore e del denominatore e passando al limite. Si ha subito:

lim_h→o sinh/h =lim_h→o cos h/1 = 1

Magnifico? No, assolutamente no! Come facciamo a sapere quanto vale la derivata di sen h se è proprio quello che stiamo cercando? Eh no, dobbiamo seguire un'altra strada... In altre parole dobbiamo ricavare il limite di sin h/h in altro modo, per poi poter proseguire.

Ricapitoliamo: siamo partiti dal rapporto incrementale di sin x ma ci siamo fermati davanti al limite di sin h/h. Per superare questo ostacolo abbiamo applicato la regola di De l'Hopital, il che però comporta la conoscenza della derivata di sin h. Non c'è che dire, il gatto si morde proprio la coda: Per trovare la derivata di sin h abbiamo bisogno di calcolare il limite di sin h/h, ma per determinare il limite di sin h/h abbiamo bisogno di conoscere la derivata di sin h.

Ed ecco quindi la necessità di ricavare il limite di sin x/x attraverso un altro metodo. Noi useremo quello geometrico, sapendo che avremo a disposizione un risultato di estrema importanza, il limite NOTEVOLE di sin x/x, utile in molti altri casi.

Limite di sin x/x

La cosa migliore da fare? Calcolare il limite di partenza per via puramente geometrica.

Consideriamo in Fig. 1 il cerchio di raggio r unitario (r = 1).

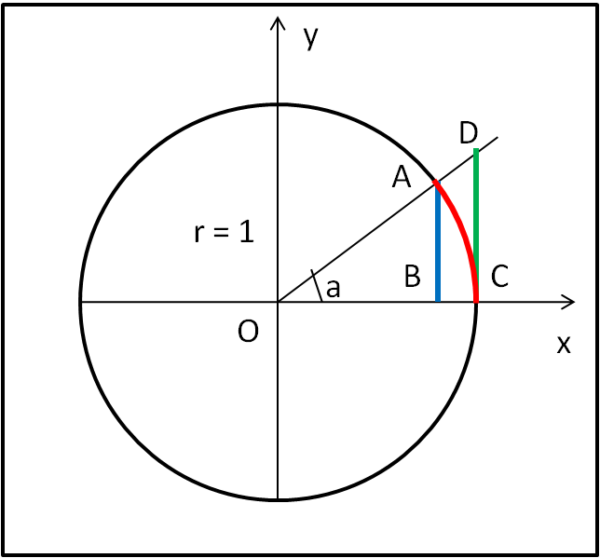
Prendiamo un angolo a che tenda a 0 positivo (0⁺), ossia che si avvicini a 0 provenendo dalla parte positiva. In tal modo siamo sicuri che tutte le grandezze che andiamo a calcolare sono positive.

AB = sin a

AC = r a = 1 a = a            (arco di cerchio)

DC = tan a

Risulta immediata la relazione:

AB ≤ AC ≤ DC

sin a ≤ a ≤ tan a

Essendo le grandezze positive posso prendere il loro reciproco e invertire l'ordine delle disuguaglianze:

1/sin a ≥ 1/a ≥ cos a/sin a

A questo punto posso moltiplicare le tre grandezze per una quantità positiva (sin a) senza cambiare le disuguaglianze

sin a/sin a ≥ sin a/a ≥ cos a sin a/sin a

1 ≥ sin a/a ≥ cos a

Adesso possiamo passare ai limiti per a che tende a 0⁺

lim_a→0+1 ≥ lim_a→0+sin a/a ≥ lim_a→0+cos a

1 ≥ lim_a→0+sin a/a ≥ 1

Ne segue perciò che:

lim_a→0+sin a/a = 1

Non ci resta che provare anche per a che tende a 0^-

La cosa è velocissima...

lim_a→0-sin a/a

Può essere scritto come

sin 0^-/0^-  =  - sin(0⁺)/- (0⁺) = sin 0⁺/0⁺

Ne segue che il limite per a che tende a 0^- è identico al limite che tende a 0⁺, per il quale abbiamo già trovato il risultato. Per cui:

lim_a→0sin a/a = 1

Teniamolo bene a mente!

 

Il limite trovato ci permette di tornare al calcolo della derivata del seno (1).

d(sin x)/dx = sin x lim_{h →0} (cos h -1)/h + cos x lim_h→0sin h/h

d(sin x)/dx = sin x lim_{h →0} (cos h - 1)/h + cos x · 1                .... (2)

In realtà ci rimane da calcolare il primo limite che è ancora una forma 0/0. Potremmo risolvere anch'esso per via geometrica, ma possiamo farlo anche con un piccolo trucchetto...

Sappiamo ormai che:

lim_h→0sin h/h = 1

quadriamo entrambi i membri

lim_h→0sin h²/h² = 1

Ma è ben noto che sin²h + cos²h = 1

ossia:

sin² h = 1 - cos ² h

sostituendo, abbiamo

lim_h→0 (1 - cos ²h)/h² = 1

lim_h→0 (1 - cos h)/h · lim_{h→0 ⁽}1 + cos h)/h = 1

lim _h→0 (1 - cos h)/h = 1/(lim_{h→0 ⁽}1 + cos h)/h = lim_h→0h/(1 + cos h) = 0/2 = 0

Per cui il nostro limite indeterminato diventa

lim _h→0 ((1 - cos h)/h) = 0

Notiamo che scrivere (1 - cos h) o (cos h - 1) è la stessa identica cosa dato che il risultato vale 0

Tornando alla nostra derivata (2), mettendo a frutto quanto appena ricavato, abbiamo:

d(sin x)/dx= sin x lim_{h →0} (cos h - 1)/h + cos x

d(sin x)/dx = sin x · 0 + cos x

d(sin x)/dx = cos x

 

Gli articoli dedicati alle derivate delle funzioni fondamentali sono disponibili QUI

e fanno parte del corso completo di matematica