La risposta di Maurizio è sostanzialmente corretta (l'angolo , infatti, vale proprio 150°), ma si è basata su un caso particolare, quello in cui le diagonali dell'aquilone sono parallele ai lati del quadrato ed uguali ad esso. Come, invece, ha fatto notare Fabrizio, il caso più generale comporta diagonali maggiori del lato del quadrato e, quindi, è necessario DIMOSTRARE che le diagonali sono uguali tra loro.

La figura diventa la Fig. 1

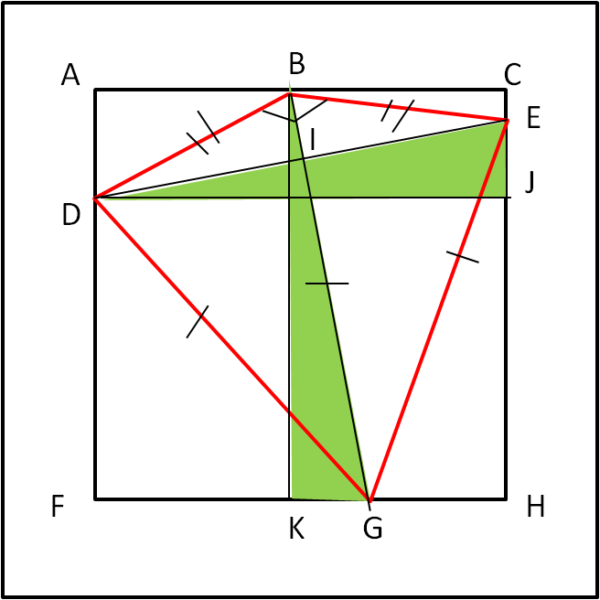
In questo caso non possiamo più dire che le diagonali sono uguali in quanto uguali al lato del quadrato. Tuttavia, non è difficile dimostrare che le diagonali, pur essendo maggiori del lato, continuano a restare uguali tra loro.

Disegniamo, infatti, i due triangoli verdi nella Fig. 1. Essi sono congruenti, dato che gli angoli in K e J sono entrambi retti per costruzione. BK = DJ dato che entrambi sono uguali al lato del quadrato. Infine, le due diagonali dell'aquilone sono  perpendicolari tra loro. Ciò significa che gli angoli che formano con altre due rette perpendicolari tra loro devono essere uguali. Ne segue che gli angoli in B e D devono essere congruenti. In conclusione i due triangoli verdi devono essere congruenti. Ma, essendo congruenti, le loro ipotenuse sono congruenti, ossia:

DE = BG

Le due diagonali dell'aquilone, perciò, pur non essendo uguali al lato del quadrato, restano comunque uguali tra loro.

Un'ipotesi di partenza diceva che GB = GD = GE. Adesso abbiamo dimostrato che DE = BG. Possiamo concludere che:

DG = DE = GE, ossia il triangolo DEG è equilatero e, quindi, l'angolo in G deve essere di 60 °. Inoltre, sappiamo che i due triangoli DGB e BGE sono congruenti (i tre lati sono uguali) e isosceli. Ne segue che angolo DGB = 30°. Chiamiamo x l'angolo DBG che è la metà dell'angolo che vogliamo trovare. Essendo il triangolo DGB isoscele, DBG = GDB = x, possiamo scrivere:

x + x + 30° = 180°

2x = 150°

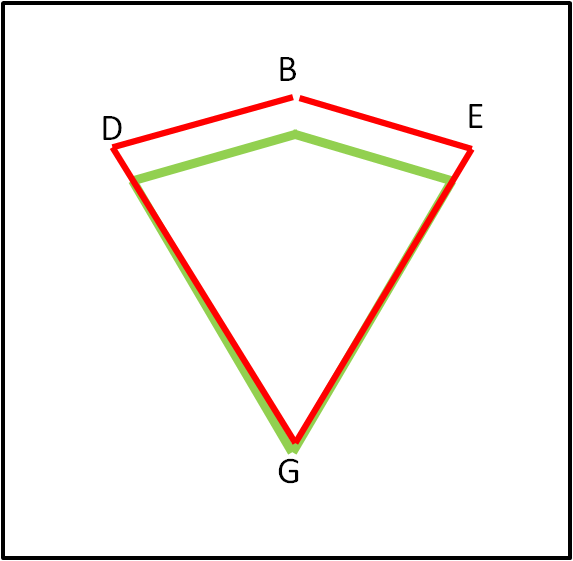
E' piuttosto simpatico il fatto che anche ne caso generale l'angolo incognito rimane 150° come nel caso particolare descritto correttamente da Maurizio. Possiamo concludere che il nostro aquilone si allarga, ma mantiene l'angolo in B uguale. Qualcosa come quello che abbiamo disegnato in Fig. 2.

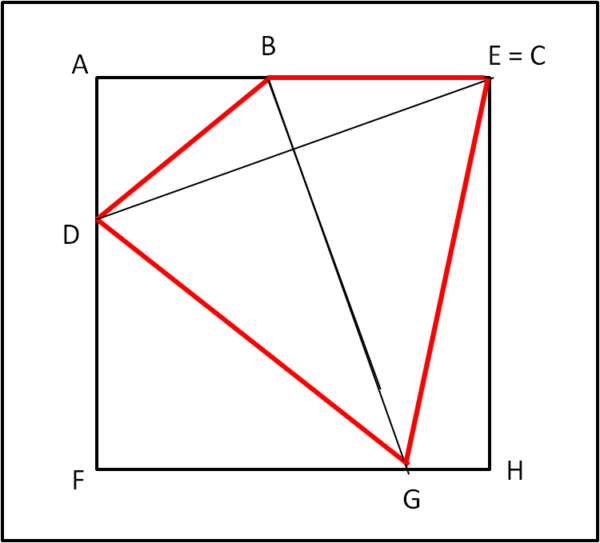
Il caso limite, con grandezza massima, dovrebbe essere quello in cui il lato BC si sovrappone a BE, come mostra la Fig. 3.

Insomma, questi aquiloni sono veramente pieni di sorprese. Un bravo a Fabrizio, ma anche a Maurizio!