(QI) Due cerchi in un ... tunnel (con soluzione) **
Abbiamo un semicerchio di raggio sconosciuto, dentro al quale sono contenuti due cerchi uguali, anch'essi di raggio sconosciuto. I due cerchi possono essere comunque piazzati, sul diametro orizzontale del semicerchio.
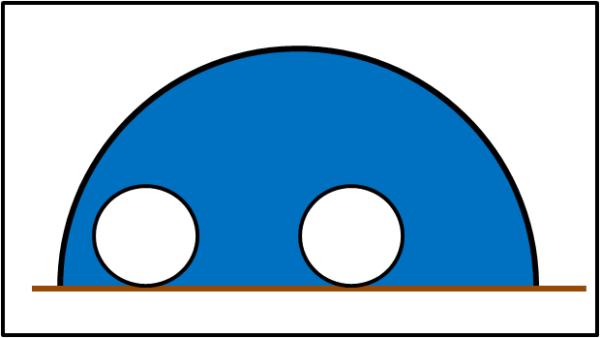
Sfortunatamente possiamo misurare la lunghezza di un solo segmento!
Riusciamo, in qualche modo, a determinare esattamente l'area azzurra?
Soluzione
Come dimostrato da Fabrizio non vi era nessun bisogno di spostare i cerchi piccoli: bastava tracciare una retta orizzontale che fosse tangente a entrambi. La lunghezza del segmento ottenuto tra i punti d'incontro della retta e il cerchio grande era più che sufficiente per risolvere il quiz. I vari passaggi sono spiegati perfettamente nel commento di Fabrizio.






4 commenti
Chiamo con R il raggio (incognito) del semicerchio grande.
con r i raggi (incogniti) dei due cerchi piccoli che possono rotolare sul diametro orizzontale del cerchi grande.
con d il segmento che unisce i centri dei due cerchi piccoli.
se faccio rotolare i due cerchi piccoli in modo che le verticali condotte dai loro centri si intersichino con gli estremi del diametro del centro grande misurando d ottengo;
d = 2R da cui R = d/2
poi faccio rotolare i due cerchi piccoli in modo che le loro circonferenze intersichino gli estremi del diametro del cerchio grande e misuro la distanza tra i loro centri che chiamo l ho:
l + 2r = 2R da cui ricavo r = R - l/2
ora posso calcolare la superficie blu del semicerchio grande come differenza tra la sua superficie e quella dei due cerchi piccoli ottenendo
blu = π (d/2)2/2 - 2 (π (R - l/2)2)
Dalla figura precedente si posiziona uno dei due cerchietti in modo che un estremo B del diametro AB coincida con l'estremo sinistro del semicerchio e facendo in modo che la perpendicolare dell'altro punto A unisca il centro del cerchio grande.
Si misura AC. L'area blu sarà uguale a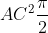
Infatti l'area blu è data dalla differenza tra l'area del semicerchio di rggio R e le due aree dei cerchietti piccoli di diametro d= 2r.
A =)
Essendo ABC triangolo rettangolo, il termine fra parentesi è il quadrato del cateto AC.
A prima vista sembrerebbe che dobbiamo trovare due incognite (il raggio del cerchio grande e quello dei cerchi piccoli) con una sola misura. Non sembrerebbe possibile, a meno che le incognite non siano veramente due. Da qui mi è venuto lo spunto per la soluzione che propongo.
Sono costretto a ripetere che i cerchi piccoli SONO CONTENUTI nel cerchio grande. Non posso farli uscire...