Questo articolo è inserito in Dinamica e Meccanica

Una soluzione tecnologica di estrema semplicità ha permesso di far correre i treni su due stretti binari senza farli deragliare, soprattutto in curva. Vediamo di descriverla in modo puramente geometrico

(1) Dove si "elimina" il cilindro 

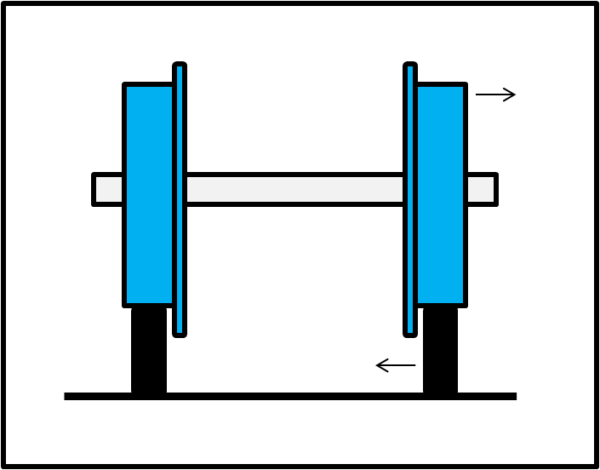
Sappiamo tutti che un treno viaggia su due rotaie, i cui i binari sono piuttosto stretti. A prima vista sembrerebbe una situazione molto pericolosa, dato che basterebbe un leggero spostamento laterale ed ecco che il treno uscirebbe dal suo percorso obbligato, con le tragiche conseguenze del caso. I più attenti si saranno accorti che le ruote hanno due cerchi più grandi ai loro estremi in modo da vietare l'uscita dai binari. Qualcosa come quello mostrato in Fig. 1.

Le due ruote, a sezione cilindrica, sono solidali tra loro e con l'asse che le sostiene (ruote e asse ruotano in perfetto accordo). Un leggero spostamento delle ruote verso un lato o l'altro dei binari verrebbe bloccato dai due cerchi di raggio maggiore posti alle loro estremità. Perfetto?

Non tanto direi... fidarsi solo di quei due cerchi aggiuntivi sarebbe alquanto rischioso e, se non altro, si andrebbe incontro a una rapida usura del materiale dovuto allo sfregamento. Sarebbe molto meglio usarli solo come protezione aggiuntiva e affidare il compito di mantenere l'assetto ideale a qualcosa di più sicuro che sia in grado di AUTOCORREGGERSI.

Non parliamo poi di quello che succederebbe in curva... La ruota più interna dovrebbe percorrere un tragitto più corto di quello della ruota esterna, ma se le ruote sono solidali tra loro ciò non sarebbe possibile: i treni non hanno il differenziale come le automobili! In poche parole, il treno tenderebbe ad andare dritto e i due "blocchi" laterali non potrebbero certo permettere di mantenere una minima stabilità in curva. Succederebbe una vera catastrofe come mostra la Fig. 2 in cui si riporta la visione dall'alto: il treno uscirebbe comunque dai binari.

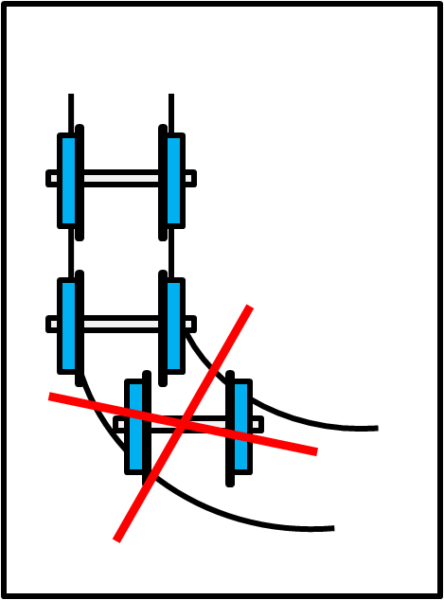
Niente da fare, sembra proprio che le ruote cilindriche non siano la scelta migliore. Discutiamo, allora, un po' di geometria.

(2) Dove ci si dedica al tronco di cono

L'unica strada che ci rimane è quella di escludere le ruote cilindriche, proprio quelle che sembrano permettere la massima stabilità. Ma, purtroppo, il treno deve curvare...

Analizziamo allora più attentamente come rotola un cilindro e un tronco di cono. Lo facciamo in Fig. 3.

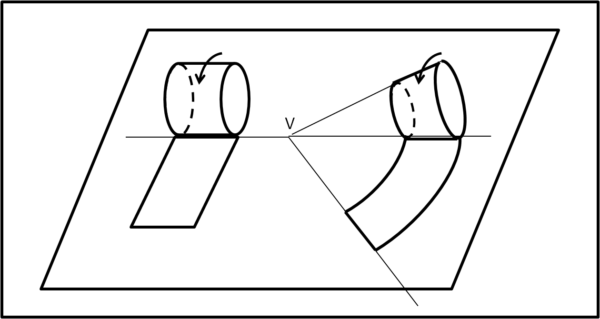
Per simulare il rotolamento su un piano basta vedere cosa succede se "apriamo" la nostra figura e la sviluppiamo su di esso. A sinistra abbiamo il cilindro che, come previsto, permette un moto rettilineo uniforme. A destra abbiamo un tronco di cono. Il suo sviluppo mostra come la superficie ottenuta e, quindi, il suo rotolamento, descriva un arco di curva. Immaginiamo di prendere un cono e di vincolare la posizione del suo vertice. Il rotolamento sarebbe proprio quello mostrato in figura. Rispetto al sistema solidale con il vertice, il cono e, di conseguenza anche il tronco di cono, descrive una traiettoria curva. In altre parole l'estremo di sinistra del tronco di cono descrive un tratto curvilineo più corto di quello esterno. Se le parole non bastano, prendete un bicchiere di carta e fatelo rotolare: la pratica dimostrerà i fatti molto chiaramente.

Il tronco di cono sembrerebbe essere ancora peggio del cilindro: non funzionerebbe nemmeno su un rettilineo.  Ma ne siamo proprio sicuri?

(3) Dove si raddoppia il tronco di cono

Immaginiamo di dare alle ruote del treno una forma a tronco di cono. Abbiamo due possibilità: la parte più grande del tronco di cono sta all'esterno oppure all'interno. Possiamo facilmente studiare il comportamento utilizzando due bicchieri di carta e unirli tra di loro, incollando tra loro le basi maggiori oppure le basi minori. Otteniamo i due solidi (a) e (b) nella parte alta di Fig. 4.

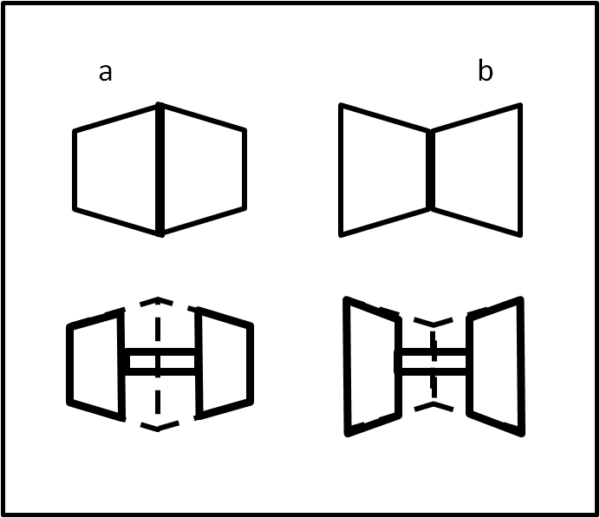
Mi direte subito : "Ma che c'entrano con le ruote di un treno?", Beh... semplice, basta tagliare la parte interna dei due solidi e ottenere proprio i nostri due tipi di ruota, come mostra la parte bassa di Fig. 4. Permettetemi, perciò, di utilizzare ancora i solidi di Fig. 4 per il prossimo esperimento, dato che il risultato sarà del tutto identico a quello delle due ruote separate.

(4) Dove un piano inclinato risolve il problema.

Seguendo le orma di Galileo, costruiamo un piano inclinato formato da due binari e facciamo rotolare i due solidi su di esso, come mostra la Fig. 5.

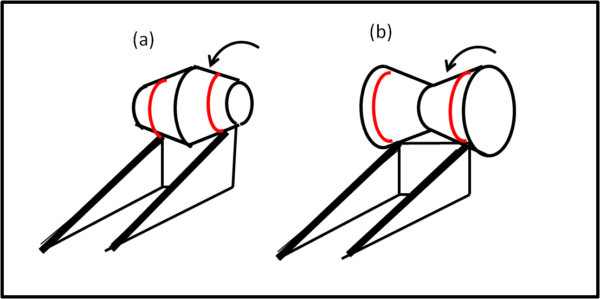
Anzi, prima di eseguire l'esperimento, ragioniamo sul possibile vincitore. Non vi è dubbio che il caso (b) (ruote con il cerchio più piccolo verso l'interno) sembra decisamente più stabile di quello con i cerchi più grandi verso l'interno. Proviamo a metterli su un tavolo e ci accorgiamo subito che (b) rimane nella stessa posizione anche se gli diamo un leggero colpo laterale. Il caso (a), invece, si inclina immediatamente. Il caso (b) mostra un equilibrio stabile, mentre (a) lo mostra instabile. Però, però, stiamo parlando di equilibrio statico. vediamo il tutto in movimento, utilizzando il nostro piano inclinato.

Facciamo rotolare la nostra coppia di bicchieri. Per controllare la configurazione più stabile spostiamo leggermente  il sistema verso destra o sinistra, come preferite.

Il caso (b) porta a una rapida uscita del doppio tronco di cono, mentre il caso (a) arriva in fondo senza problemi, in posizione migliore di quando era partito. Come mai? Potete provare con i due bicchieri, ma questa situazione si ripete ogni volta. Il caso (a) è quello che garantisce una perfetta stabilità nel suo movimento. Cosa è successo? Per capirlo, guardiamo frontalmente le due discese e notiamo la "splendida" autocorrezione.

(5) Dove si preferisce  il doppio tronco di cono dalla forma a "barile"

Disegniamo la Fig. 6 che riporta una visione dall'alto.

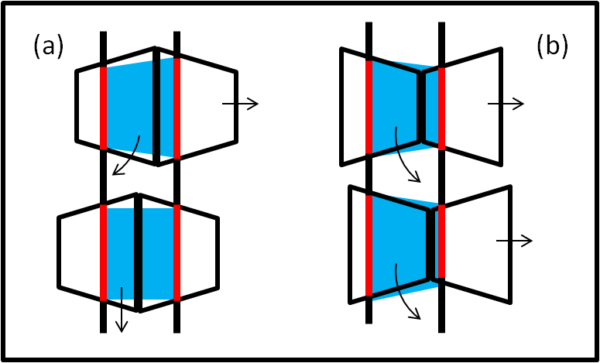
Spostiamo sia (a) che (b) leggermente verso destra, in modo da simulare un piccolo errore. Nel caso (a), la circonferenza di contatto con il binario di sinistra è inizialmente più piccola di quella di destra. Questo fatto significa che ciò che stiamo facendo rotolare non è un cilindro, ma il tronco di cono che abbiamo colorato in azzurro. Ciò comporta che il nostro doppio bicchiere tende a rotolare verso sinistra rispetto ai binari rettilinei, ossia verso una situazione di perfetto equilibrio (sezione azzurra perfettamente cilindrica). Nel caso (b), invece, le cose non funzionano affatto.  Otteniamo nuovamente un tronco di cono azzurro, ma, questa volta, la circonferenza di contatto maggiore è quella di sinistra. Ne segue che il doppio tronco di cono  tende a rotolare verso destra, peggiorando la situazione fino alla inevitabile fuoriuscita dai binari.

Attenzione: non confondiamo le due parti del solido (trochi di cono) con il tronco di cono che ha per basi le due circonferenze di contatto. Resta il fatto, comunque, che la possibilità di ottenere quest'ultimo tronco di cono deriva dall'avere scelto due tronchi di cono affiancati come solido in rotolamento.

(6) Dove si cerca di curvare

Bene... tutto risolto per il moto rettilineo, ma resta ancora aperto il problema, non certo banale, delle curve. Eh no, cari amici! Le due ruote a tronco di cono risolvono brillantemente anche questo problema. Vediamo il perché in Fig. 7.

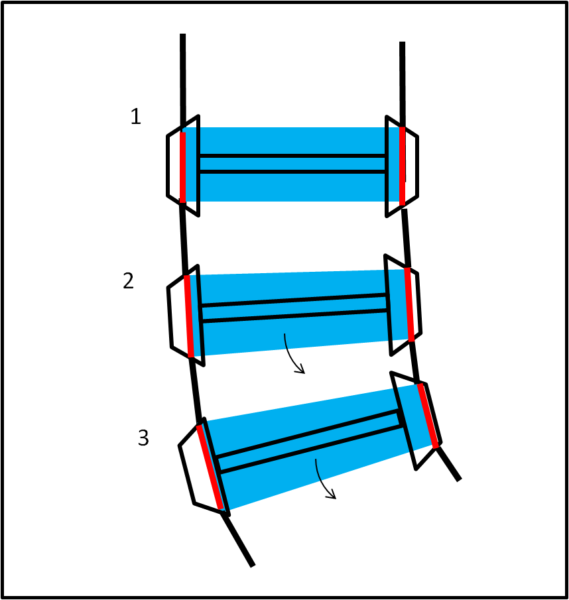
Tra la situazione (1) e la (2) inizia la curva. Le ruote tenderebbero ad andare dritte, ossia a spostarsi leggermente verso sinistra rispetto ai binari. Facendo questo, però, la circonferenza di contatto della ruota di sinistra diventa più grande di quella di destra. Il cilindro delimitato dalle due circonferenze si trasforma subito nel tronco di cono azzurro e inizia a rotolare spostandosi verso destra. Lo spostamento continua e ci accorgiamo che la traiettoria delle ruote segue perfettamente la curva. Si raggiunge l'equilibrio e il tronco di cono azzurro permette alle ruote di continuare a seguire i binari senza rischi di deragliamento.

Magnifico! Ovviamente, non possiamo pretendere curve troppo strette o velocità troppo elevate, ma il tutto funziona perfettamente. Per garantirci una maggiore sicurezza, abbiamo anche i due cerchi più grandi da inserire nella sezione più grande dei due tronchi di cono. In poche parole, le ruote auto stabilizzano il loro movimento. Una soluzione geometrica semplice, ma veramente geniale!

Finora abbiamo visto il tutto dall'alto, ma il tronco di cono azzurro deve vedersi anche frontalmente e la Fig. 8 ci mostra la configurazione durante la curva. Noi non ce ne accorgiamo, ma tutto il treno si inclina leggermente.

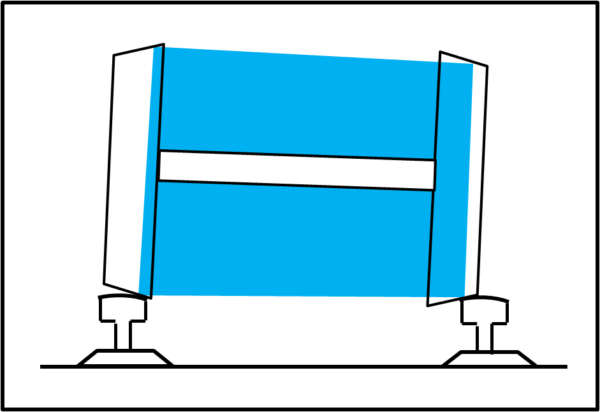
La trattazione è stata semplificata al massimo senza bisogno di introdurre forze e cose del genere. In realtà, il tutto viene aiutato dalla forma a "fungo", dei binari e dalla loro leggerissima inclinazione verso l'interno, soprattutto per avere una maggiore superficie d'appoggio tra ruote e binari.

D'ora in poi, quando prenderete il treno, pensate con al tronco di cono che, con il suo moto curvo, riesce a farvi viaggiare con sicurezza senza uscire dai binari. Potenza della geometria!