Categorie: Matematica
Tags: corde geometria piana quiz tre cerchi
Scritto da: Vincenzo Zappalà
Commenti:30
(QI) Il problema dei tre cerchi ***
Voglio presentarvi un simpatico problema piano legato alla convivenza di tre cerchi qualsiasi, che si intersecano vicendevolmente. Lo presento come "quiz", ma vedremo che servirà a introdurre due nuove definizioni e aprirà la strada a interessanti casi particolari. Insomma, tre cerchi ne possono "combinare" delle belle...
Il problema è illustrato in Fig. 1.
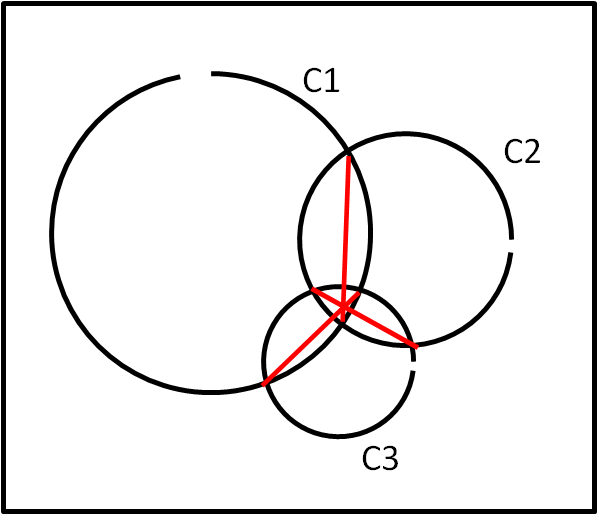
Prendiamo tre cerchi di raggio diverso e facciamoli intersecare a due a due. Tracciamo le corde individuate da ciascuna coppia di punti di contatto tra i due cerchi. Esse si incontrano in un solo punto (provare per credere).
Bene... la domanda è molto semplice:
Perché succede questo fatto?
In altre parole, dimostrare rigorosamente, rimanendo sul piano del foglio, che le tre corde si intersecano in un punto
Ritengo che non sia un quiz banale come potrebbe apparire a prima vista (penso, inoltre, che abbia varie possibilità di soluzione). Il metodo che ho usato, in particolare, abbisogna di alcuni concetti non generalmente conosciuti (noi ne abbiamo parlato... ma, di sicuro, non vi dico COME e QUANDO).
Mi aspetto soluzioni diverse e spunti per la prosecuzione dell'argomento.
QUI l'articolo con varie soluzioni






30 commenti
Caro Enzo,
il punto d'incontro delle tre corde sembra essere "parente stretto" dell'ortocentro relativo al triangolo avente per vertici i 3 centri delle rispettive circonferenze. Mi spiego meglio con una figura:
Se traccio le parallele ad x, y, z che chiamo x', y', z' passanti per i vertici del triangolo OO'O'' , queste ultime saranno parimenti perpendicolari ai segmenti OO' , O'O'' , O''O, lati del triangolo OO'O'' , rappresentando quindi 3 segmenti dove giacciono le tre altezze del suddetto triangolo e che si incontrano in un punto che è l'ortocentro del triangolo.
Praticamente il sistema di assi xyz (che sono le tre corde) si può considerare come un sistema traslato del sistema di assi x'y'z' (dove giacciono le 3 altezze).
Le tre corde possono essere viste come i tre assi radicali. L'equazione dell'asse radicale tra due circonferenze si ricava facendo la differenza tra le equazioni delle due circonferenze. Nel nostro caso:
circonf.1) x^2+y^2+ax+by+c=0
circonf.2) x^2+y^2+dx+ey+f=0
circonf.3) x^2+y^2+gx+hy+m=0
sottraendo la 2) dalla 1): (a-d)x+(b-e)y+(c-f)=0
sottraendo la 3) dalla 1): (a-g)x+(b-h)y+(c-m)=0
sottraendo la 3) dalla 2): (d-g)x+(e-h)y+(f-m)=0
Si puo' notare che l'ultima equazione e' la differenza tra seconda e la prima, cioe' non e' indipendente dalle prime due. Allora le tre rette (assi radicali) appartengono a un fascio di rette, in questo caso fascio proprio. Quindi le tre corde si incontrano in uno stesso punto.
Caro Andy,
c'è qualcosa che non torna nella tua dimostrazione... Tu dici:
Se traccio le parallele ad x, y, z che chiamo x', y', z' passanti per i vertici del triangolo OO'O'' , queste ultime saranno parimenti perpendicolari ai segmenti OO' , O'O'' , O''O, lati del triangolo OO'O'' , rappresentando quindi 3 segmenti dove giacciono le tre altezze del suddetto triangolo e che si incontrano in un punto che è l'ortocentro del triangolo.
Tre segmenti paralleli a tre segmenti che si incontrano in un punto (ortocentro) non è detto che si intersechino in un punto.
Caro Artù...
non correre, ti prego: non tutti sanno cosa sono gli assi radicali. Tu sei sulla giusta strada, ma forse bisognerebbe il tutto spiegando meglio i vari passaggi...
caro Andy,
ho riletto attentamente il tuo metodo. Devo dire che in realtà la traslazione funziona, ma sono ancora incerto sul fatto che sia una dimostrazione accettabile. Come dimostrare che esiste sempre questa traslazione? Cerca di convincermi di più...
Ci provo, mentre attendo in auto (ferma) a Taranto.. L'asse radicale di due circonferenze intercesantesi in due punti e' la retta passante per tali due punti. Come si fa quando in geometria analitica, si vogliono trovare eventuali punti di intersezione tra due curve, mettiamo a sistema le equazioni delle due circonderenze. Sottraendo la seconda dalla prima, ottengo l'equazione:
(a-d)x+(b-e)y+(c-f)=0
che e' l'equazione di una retta. In particolare e' l'equazione della retta passante per i due punti di intersezione tra le due circonferenze. Cioe' e' l'equazione dell'asse radicale tra le due circonferenze.
Si ripete il ragionamento per le altre due coppie di circonferenze, la prima con la terza e la seconda con la terza, trovando le equazioni degli altri due assi radicali.
Poi si nota che l'equazione del terzo asse radicale e' combinazione di quelle degli altri due assi. Cio' fa si che una coppia di coordinate (x,y) che soddisfi le prime due equazioni, soddisfa anche la terza. Cioe' , in pratica, che per il punto di intersezione dei primi due assi radicali, passa anche il terzo. Cioe', infine, che le tre corde del nostro problema si incontrano in uno stesso punto.
Cari Andy e Artù,
faccio alcuni commenti...
(1) per Andy: devo ammettere che il tuo metodo è estremamente interessante dal punto di vista grafico. Ottenuto il triangolo è poi facile spostarlo fino a far sì che i suoi vertici stiano sulle corde iniziali. Però,, mi piacerebbe sapere come ottenere (non graficamente) la traslazione necessaria.
(2) per Artù: stai seguendo il metodo che avevo in testa io... però l'ultima parte quella delle combinazione delle due mi sembra un po' vaga.
Il problema dei tre cerchi dà luogo a moltissime configurazioni e a tanti teoremi, sarebbe perciò molto bello che ognuno di voi esponesse con tutti i passaggi ciò che si deve fare per arrivare alla conclusione. Li pubblicherei insieme alla mia che si rifà alla potenza di un punto.
Inoltre, essendo Artù un ben noto esperto in 3D, mi piacerebbe che tirasse fuori un metodo ulteriore che si basa sullo spostamento del problema piano a quello in 3D. Un metodo immediato...
Insomma, per non stancare troppo l'occhio vi faccio lavorare!
Sono ancora a Taranto...
"Inoltre, essendo Artù un ben noto esperto in 3D, mi piacerebbe che tirasse fuori un metodo ulteriore che si basa sullo spostamento del problema piano a quello in 3D. Un metodo immediato..."
In pratica... date tre sfere che si intersecano a due a due, dimostrare che i tre piani radicali si intersecano in una stessa retta. Oddio, ho gia' il mal di testa
Finalmente a casa..
Riprendendo il ragionamento sulle tre corde del problema, che ho considerato come segmenti dei rispettivi tre assi cardinali delle tre circonferenze date, se dimostro che esse appartengono ad uno stesso fascio proprio di rette (che per definizione ha un unico punto in cui si incontranno tutte le infinite rette del fascio) ho risolto il problema.
Ho già scritto, nei precedenti commenti, come ricavare le equazioni dei tre assi cardinali. Una volta trovate, potrei procedere con il ricavare le coordinate del punto di intersezione tra i primi due assi cardinali e poi andare a sostituire queste coordinate nell'equazione del terzo asse e constatare che esse la soddisfano (problema risolto). Oppure (e io preferisco questa strada perchè l'altra richiede più calcoli) posso ricordarmi che l'equazione di un fascio proprio di rette di equazioni ax+by+c=0 e dx+ey+f=0 si ottiene con una combinazione lineare delle due suddette equazioni:
ax+by+c+k (dx+ey+f)=0
essendo k un parametro al variare del quale ottengo le infinite rette del fascio proprio. Spiegai questa cosa in questo articolo:
http://www.infinitoteatrodelcosmo.it/2016/06/25/introduzione-alla-geometria-dello-spazio-seconda-parte/
Nel nostro caso, le due rette che utilizzo per definire il fascio hanno equazione (vedere miei commenti precedenti):
(a-d)x+(b-e)y+(c-f)=0
(a-g)x+(b-h)y+(c-m)=0
Pertanto, l'equazione del fascio proprio di rette sarà:
(a-d)x+(b-e)y+(c-f)+k [(a-g)x+(b-h)y+(c-m)]=0 (1)
Allora, se dalla (1) riesco a ricavare, per un particolare valore di k, l'equazione del terzo asse radicale, allora avrò dimostrato che anche questa retta appartiene allo stesso fascio proprio definito dalle prime due. Cioè avrò dimostrato che i tre assi cardinali, ossia in ultima analisi le tre corde del problema, passano per uno stesso punto.
Pongo allora k=-1. La (1) diventa:
(a-d)x+(b-e)y+(c-f)-(a-g)x-(b-h)y-(c-m)=0
cioè
(a-d-a+g)x+(b-e-b+h)y+(c-f-c+m)=0
cioè
-(d-g)x-(e-h)y-(f-m)=0
ossia
(d-g)x+(e-h)y+(f-m)=0
Ed ecco spuntare fuori proprio l'equazione del terzo asse radicale ! Anche esso appartiene al fascio proprio definito dai primi due. Quindi il punto di interezione delle tre rette è lo stesso. Problema risolto.
cominciamo con Artù...
Beh, la sua dimostrazione funziona, anche se -forse- si potrebbe semplificare usando la potenza di un punto rispetto a una circonferenza In tal modo basterebbe solo dimostrare che l'asse radicale è proprio la retta che passa per i due punti intersezione. Artù l'ha data come definizione di asse radicale, ma sarebbe meglio introdurre l'asse radicale di due circonferenze il luogo dei punti che hanno la stessa potenza rispetto a entrambe (si generalizza quindi, anche a circonferenze che non si intersecano). Quando una potenza vale zero deve valere zero anche per l'altra, da cui segue che i due punti intersezione stanno sull'asse radicale. Presa un'altra coppia di circonferenza trovo un altro asse radicale che ha un punto in comune col primo. Ne segue che questo punto ha la stessa potenza rispetto a tutte e tre le circonferenze, per cui deve essere unico. Se A uguale a B e B uguale a C, C deve essere uguale ad A...
Passiamo ad Andy,
forse mi sbaglio, ma il suo metodo ha solo spostato l'incognita. Infatti, il suo triangolo, mediante traslazione, può essere trasportato con i vertici sulle corde intersezione. Ma, il problema è ora di dimostrare che ciò può accadere. Il fatto che capiti spostando materialmente il triangolo e trovando la soluzione non differisce dal fatto che tracciando le tre corde troviamo graficamente un solo punto.
Cosa ne pensate?
Per il problema in 3D...
Stesso metodo. Le equazioni delle tre sfere in un sistema di assi cartesiani x,y,z sono:
1) x^2+y^2+z^2+ax+by+cz+d=0
2) x^2+y^2+z^2+ex+fy+gz+h=0
3) x^2+y^2+z^2+lx+my+nz+p=0
Quando due sfere si intersecano, la curva di intersezione è una circonferenza appartenente ad un piano che è in pratica l'quivalente nello spazio dell'asse radicale nel piano. Trovo l'equazione di tale piano mettendo a sistema le equazioni delle due sfere che si intersecano e trovo, rispettivaemte:
(a-e)x+(b-f)y+(c-g)z+(d-h)=0 (piano tra le due sfere 1) e 2) (1)
(a-l)x+(b-m)y+(c-n)z+(d-p)=0 (piano tra le due sfere 1) e 3) (2)
(e-l)x+(f-m)y+(g-n)z+(h-p)=0 (piano tra le due sfere 2) e 3) (3)
Ora mi accorgo che la (3) è combinazione lineare delle (1) e (2). Allora, per le considerazioni fatte nel caso piano (lì avevamo fascio proprio di rette, qui abbiamo fascio proprio di piani), il piano tra le circonferenze 2) e 3) appartiene al fascio proprio di piani definito dai primi due piani. Quindi, i tre piani passano per una stessa retta.
Manca solo una bella figura per rendere meglio il concetto.
Chissa cosa accadrebbe nello spazio quadridimensionale x,y,z,t....
In realtà, caro Artù, il sistema delle tre sfere non ha bisogno di calcoli.. Basta prendere le tre sfere in modo che abbiano i centri su uno stesso piano. Le tre sfere si intersecano secondo i piani che hai detto tu, ma questi tre piani devono per forza avere una retta in comune perpendicolare al piano dei centri. I tre piani sono in realtà individuati dai tre cerchi intersezione che, visti dall'alto, danno proprio le tre rette. E' come se si prendessero tre bolle di sapone e si facessero compenetrare tra loro. Viste dall'alto danno p0roprio la figura del piano.
Non è facile visualizzare quanto detto, ma forse tu ci potresti riuscire.. sei o non sei un mago delle 3D ????
si può fare di meglio, ma mi attende, a minuti, il corso di aggioramento sulla sicurezza del lavoro nei cantieri...
Caro Enzo,
cercherò di essere più chiaro partendo da una figura:
che è la stessa figura postata prima ma eliminando le circonferenze per utilità visuale.
Il triangolo di vertici OO'O'' (con O, O', O'' centri delle circonferenze originarie) è uno e uno solo (relativo ovviamente alla disposizione delle tre circonferenze) e non trasla.
Se prima traccio le altezze di tale triangolo (x' , y' , z'), che si incontrano in un punto unico definito come ortocentro, equivale a dire che delle infinite rette del fascio passante per il punto definito ortocentro, solo 3 di queste avranno le caratteristiche:
di essere perpendicolari ai lati del triangolo;
e passanti per ogni vertice opposto al singolo lato del triangolo;
e su queste uniche tre rette giacciono le tre altezze (in verde).
Se parimenti considero il fascio delle infinite rette che passano per il punto di intersezione delle 3 corde, solo tre avranno la caratteristica di essere contemporaneamente perpendicolari ai segmenti congiungenti, a coppie, i centri delle tre circonferenze (segmento OO' , segmento O'O'' , segmento O''O); e su queste tre rette (che coincidono con i 3 assi radicali). giaceranno le corde così come disegnate.
Ora, se l’altezza verde x’ del triangolo OO’O’’ è per definizione perpendicolare al segmento congiungente i due centri OO’, e la corda rossa x (giacente sull'asse radicale relativo alla distanza OO') è anch'essa perpendicolare ad OO', allora x' ed x sono senz'altro parallele; per lo stesso ragionamento:
y' è parallela ad y
z' è parallela a z
Se considero il sistema di tre semirette X'Y'Z' (sulle quali giacciono le altezze x' , y' , z') con origine nell'ortocentro (che è uno e uno solo), e il sistema di tre semirette XYZ (sulle quali giacciono le corde x,y,z) con origine nel punto di incontro delle tre corde, vengono rappresentati due sistemi perfettamente uguali (anche se collocati sul piano in posizioni differenti). Ma essendo uguali, se uno ammette un unico punto di incontro, allo stesso modo anche l'altro ammetterà un unico punto di incontro.
Comincio con Andy...
mi hai "quasi" convinto... Mi rimane un dubbio, però. Tu trovi che le tre rette rosse sono parallele a quelle verdi e questo mi sta bene. ma poi dici:
Se considero il sistema di tre semirette X'Y'Z' (sulle quali giacciono le altezze x' , y' , z') con origine nell'ortocentro (che è uno e uno solo), e il sistema di tre semirette XYZ (sulle quali giacciono le corde x,y,z) con origine nel punto di incontro delle tre corde,...
Ma chi mi dice che esiste un punto d'incontro di queste tre rette parallele a quelle verdi iniziali? Le rette potrebbero essere parallele ma non incontrarsi in un solo punto. Ammettere che esista questo punto è come ammettere che le tre rette rosse si incontrano in un punto che è proprio la tesi.
Ti dico la verità? Spero di sbagliarmi perché il tuo approccio mi piace tantissimo!
Caro Artù,
la tua figura è perfetta. Prendendo le tre sfere si potrebbe dimostrare visivamente (facendole avvicinare un po' alla volta) che i tre cerchi che rappresentano la loro intersezione reciproca si incontrano i due punti ? Ciò dimostrerebbe la tesi dei tre cerchi che altro non sarebbero che le proiezioni delle sfere sul piano dei loro centri.
Ancora un piccolo sforzo... ce la puoi fare!
Faccio un ragionamento per esclusione:
date le tre circonferenze intersecanti, costruito il triangolo unente i tre centri, tracciate le sue tre altezze,
per quanto già detto prima, traccio tre rette blu a caso, parallele alle altezze del triangolo e ovviamente perpendicolari ai suoi lati, tagliano delle corde nelle 3 circonferenze e si incontrano in un punto, come in figura 1:
parallelismo e perpendicolarità vengono rispettate, tagliano delle corde, ma non nei punti di mutue intersezioni delle circonferenze così come in ipotesi.
In figura 2 stesse condizioni di prima, ma rette blu che si intersecano in più di un punto:
anche qui parallelismo e perpendicolarità vengono rispettate, tagliano delle corde, ma non nei punti di mutue intersezioni delle circonferenze così come in ipotesi.
Ultimo caso in figura 3:
In questo caso, se le rette blu sono parallele alle altezze del triangolo e tagliano delle corde nei punti di intersezione delle 3 circonferenze, allora si incontrano in un solo punto.
Scusami Andy, forse sto rimbambendo, ma non sono ancora convinto... Posso accettare che due corde che passano per i punti d'intersezione di due cerchi si incontrano sicuramente in un punto. Adesso però dovrei dimostrare che la terza corda passa ancora per quel punto. Visivamente è vero, ma è proprio quello che voglio dimostrare senza costruire la figura. In pratica, se due corde intersecanti due cerchi si incontrano in punto anche la terza deve passare per quel punto... O, magari, dimostrare che se si trasla il triangolo in modo che due suoi vertici stiano sulle due corde, se ne deriva che anche il terzo vertice deve stare sulla terza corda.
Sarebbe bello se qualche altro ottimo matematico ci desse il suo parere... magari Mau o Fabrizio o Leandro o Arturo o chissà quale altro esperto si nasconde nelle pieghe del blog...
E se capovolgessimo il problema in questo modo ?
Dati tre segmenti che , per costruzione si intersecano in un punto, posso trovare i centri dei tre cerchi considerando a due per volta i segmenti come corde di un cerchio che passa per i loro 4 punti estremi.
Non esistono altri possibili cerchi all'infuori di questi tre.
Data l'arbitrarietà della scelta dei tre segmenti come lunghezza e orientamento (l'unico vincolo è che si devono intersecare in uno stesso punto) penso si possa dire che qualsiasi terna di cerchi come quella proposta implicherà l'unicità del punto di intersezione dei tre assi radicali.
(Dato che ho dormito poco può darsi che stia dicendo sciocchezze)
Aggiungo solo questa considerazione, poi mi taccio.
Anche quella di Mau sembra interessante... ma fatemi tornare al triangolo di Andy. Impostiamo la faccenda in un altro modo.
Tracciamo soltanto due corde (rosse). Esse avranno sicuramente un punto in comune. Sulla retta verde, che non sappiamo ancora se passa da quel punto, poniamo un vertice che scorre su di essa e che è formato dalle corrispondenti rette parallele, segnate in blu, alle due corde . In tal modo si possono costruire infiniti triangoli simili a quello di Andy in cui le tre corde sono le altezze. Non è ancora completata la dimostrazione, ma penso (adesso non ho tempo...) che lo stesso ragionamento si può fare per altre due corde e si dovrebbe poter dimostrare ciò che si voleva.
Ditemi qualcosa....
Ecco, lo sapevo ...
Nel mio ragionamento c'è la premessa ingannevole che dati 4 punti ( a caso) passi sempre una circonferenza (e per giunta una sola).
Ebbene, sappiamo che per tre punti passa di certo una e una sola circonferenza. MA ... per 4 punti questo non è affatto vero. Se prendiamo una coppia delle nostre corde rosse la cosa più probabile è che non si possa costruire nessuna circonferenza.
Quindi ... tutto da rifare.
Tuttavia, disegnati i cerchi e, successivamente tracciate le 3 corde rosse, penso si possa ragionare sul fatto che se una delle tre corde ( AB ) , ruotando attorno all'estremo B, non passasse più per l'incrocio delle altre due, il suo estremo A si sdoppierebbe in A' e A'' con le conseguenti contraddizioni sulla lunghezza della corda.
Una sorta di dimostrazione per assurdo.
Scusa Enzo, ma direi che hai scritto "le rette blu parallele alle corde" mentre forse intendevi "perpendicolari alle corde".
Ossia le rette blu (che sono parallele tra loro) risultano perpendicolari ad una corda. E' così ?
Proprio così caro Enzo,
la tua impostazione dovrebbe fugare ogni fraintendimento;
ho preparato una sequenza ripetuta di immagini, con il triangolo originario (congiungente i tre centri) tratteggiato, con in verde le sue altezze, un triangolo qualunque simile all'originario (in realtà ha le stesse dimensioni, ma dovrebbe funzionare lo stesso con un qualunque altro triangolo simile, anche perché qualsiasi figura è simile a se stessa) di colore blu e infine, disegnate di rosso, le rette incidenti che contengono le corde, prese alternativamente a due a due; e una freccetta dorata "segnaposto" che punta costantemente il punto di incontro delle rette:
Corretto Mau... grazie!
Sono contento Andy... avevi proprio ragione. Basta proprio prendere le corde due a due e ripetere il ragionamento senza imporre che le corde passino per uno stesso punto. In tal modo si costruisce un triangolo con le tre altezze e queste devono per forza passare per un solo punto. Non c'è nemmeno bisogno di prendere il triangolo che passa per i centri, direi...
Forse un analogo ragionamento si potrebbe fare anche con i semiassi e magari le mediane. Basta cambiare il triangolo risolutivo...
Beh... è stata proprio una bella discussione, grazie!
Se siete d'accordo, io scrivo la mia originaria che fa uso della potenza di un punto (e ve la mando)e voi preparate per bene la vostra (appena Mau si convince della sua trattazione). Poi le mettiamo insieme in un bell'articolo. Ovviamente, il discorso vale anche per Artù il quale ha usato un metodo non molto dissimile dal mio, ma potrebbe dimostrare che tre sfere si intersecano in tre cerchi che passano per un punto e poi proiettare il tutto sul piano dei centri delle sfere, ottenend9o la figura piana.
Ieri sera mi ero lanciato in un ragionamento sul circocentro (il centro della circonferenza circoscritta al triangolo) che si ottiene dalla intersezione degli assi dei lati, assi che ( è dimostrabile) convergono in un unico punto.
Ho considerato tre cerchi tangenti tra loro (il caso limite in cui gli assi radicali sono le tangenti nei punti di contatto) e il triangolo O1 O2 O3 che si forma unendo i tre centri dei cerchi.
La direzione delle tangenti rosse, perpendicolari ai lati del triangolo sono le medesime dei tre assi (linee nere). Osservando l'animazione si vede che la prima traslazione verticale, lungo il lato O1 O2, porta la linea rossa orizzontale sopra l'asse del segmento O2 O3.
La seconda traslazione avviene perpendicolarmente alla prima, scivolando lungo l'asse orizzontale e porta le altre due linee rosse a sovrapporsi ai due assi degli altri due lati.
Ora che tutte le linee rosse sono posizionate sulle linee nere la traslazione è completata e il punto di convergenza delle linee rosse coincide con il circocentro.
Come nel caso dell'intersezione tra le circonferenze, non c'è bisogno di partire dal triangolo con vertici i centri... basta costruire a due a due gli assi delle perpendicolari ed esistono infiniti triangoli simili che hanno il circocentro nel punto desiderato.
Per aggiungere carne al fuoco, prendo spunto dall'esempio proposto da Maurizio;
se si costruisce un triangolo qualsiasi i cui vertici vengono attraversati da rette che intercettano i lati opposti (o un loro prolungamento), dividendo ogni lato in due parti, queste rette prendono il nome di ceviane (dal nome dal matematico Giovanni Ceva, vissuto tra il XVII e XVIII secolo):
Ora, per l'inverso del teorema di Ceva se avviene che: (e ovviamente procedendo in verso opposto
(e ovviamente procedendo in verso opposto  o cambiando di posto i singoli moltiplicatori), allora le tre rette sono concorrenti cioè attraversano tutte uno stesso punto:
o cambiando di posto i singoli moltiplicatori), allora le tre rette sono concorrenti cioè attraversano tutte uno stesso punto:
Quindi nel caso del circocentro proposto da Maurizio (ma anche nel caso del baricentro), i lati vengono divisi in parti uguali e il loro rapporto sarà pari ad 1, ed 1 moltiplicato tre volte per se stesso fa 1 verificando la condizione.
In generale, se esiste almeno un triangolo costruito con i vertici sui tre assi radicali e il prodotto dei rapporti tra le parti di lati è uguale a 1, viene fornita la prova della concorrenza dei tre assi stessi.
Molto interessante...