Il presente articolo è inserito in Antichi Greci, che passione!

Nel VI secolo a.C., sull'isola di Samo, l'ingegnere Eupalinos di Megara fu incaricato di scavare una galleria che sarebbe servita per incanalare l'acquedotto verso la città e il suo porto. Eupalinos sapeva il fatto suo e, per velocizzare l'esecuzione e rispettare esattamente il punto di inizio e fine galleria, decise di iniziare gli scavi da entrambe le uscite. Oggi sembra facile, ma nell'antica Grecia come si poteva essere sicuri che le due squadre di scavatori si incontrassero?

Nella foto che segue vediamo un particolare dell'isola in cui è immortalato il monte che doveva essere "forato" da parte a parte.

Più interessante per noi, però, è riportare una visione dall'alto con le varie curve di livello e una visione laterale, come mostra la Fig. 1.

La distanza da percorrere non era poca (1036 metri, per l'esattezza) ed Eupalinos non aveva GPS e non poteva certo basarsi solo sulla voce per stabilire le esatte posizioni delle squadre di scavo. Però Eupalinos conosceva bene la geometria. Tra un'entrata e l'altra venne segnato un tracciato, una specie di sentiero, costruito con estrema cura, cercando di evitare qualsiasi ostacolo, rimanendo sempre alla stessa altezza (in realtà, l'altezza delle due entrate differiscono solo di pochi centimetri). Tuttavia, si trattava di uno strano sentiero, privo di curve, e composto solo da segmenti ad angolo retto tra loro, come mostra la Fig. 2.

Dopo aver stabilito il Sud e l'Est, partì da un'estremità del futuro tunnel e cominciò a muoversi in direzione dell'alta estremità, andando solo lungo queste direzioni. In poche parole, aggirò l'ostacolo offerto dalla montagna. Il suo tragitto fu piuttosto complicato, ma basato sempre su due sole direzioni di avanzamento: una linea spezzata composta da segmenti, ad angolo retto tra loro.

Pur non avendo a disposizione il precisissimo dromedario di Eratostene, non gli fu difficile misurare in "passi" o in qualche altra unità di misura, la lunghezza dell'intero percorso, stabilendo, in particolare, quanti passi aveva fatto verso Est e quanti verso Sud.  Bene, a quel punto disegnò un triangolo rettangolo (a destra nella figura) che avesse le due misure come cateti.  La direzione tra il punto di ingresso e di uscita era determinato proprio dall'ipotenusa di tale triangolo. A questo punto non fece altro che tracciare  realmente due triangoli sul terreno (di dimensioni ridotte) all'entrata e all'uscita, che fossero simili a quello disegnato.

Gli scavatori non dovevano fare altro che iniziare lo scavo seguendo la direzione dell'ipotenusa segnata sul suolo. l'incontro era pressoché certo!

Durante lo scavo si dovette fare qualche piccolo cambiamento di percorso a causa di rocce particolarmente dure, ma Eupalinos calcolò bene le deviazioni rispetto alla linea retta e ritornò su di essa mediante anche un semplice compasso. Per essere certo che le due squadre si incontrassero realmente e non procedessero parallele l'una rispetto all'altra, giunto nei pressi dell'incontro, fece adottare ad entrambe una direzione obliqua in modo da essere sicuro. La Fig. 3 ci mostra l'opera completa.

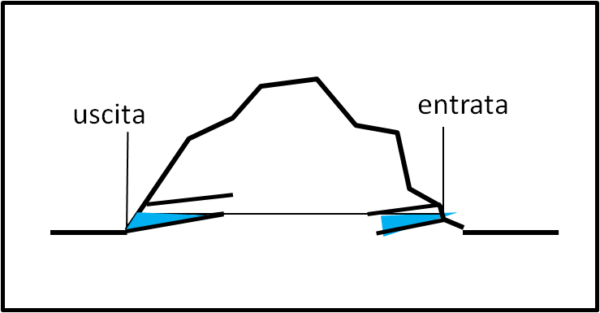
L'astuzia di Eupalinos, però, non era ancora terminata. Vi era, infatti, il problema di mantenere sempre lo stesso livello e non rischiare che una squadra andasse verso l'alto e l'altra verso il basso. Nessun problema: fece immettere acqua nel tunnel in costruzione stando ben attento che l'acqua mantenesse sempre la stessa altezza, come mostra la Fig. 4.

Che dire? Tanto di cappello Dott. Ing. Eupalinos!

Il tunnel è oggi visitabile ed è anche molto affascinante...