Il teorema della pizza */***
Pochi giorni fa si discuteva con Maurizio, al telefono, sulla bellezza e importanza della geometria. Soprattutto si notava come moltissimi problemi apparentemente solo teorici avessero poi applicazioni pratiche di grande importanza. Applicazioni nascoste a prima vista e che si sono manifestate, magari, dopo anni di studi accurati.
Tuttavia, a volte, capita il contrario, ossia ciò che viene presentato come problema pratico potrebbe avere soluzioni più semplici e immediate.
Facciamone un classico esempio: il teorema della pizza. Più pratico e invitante di così...
Esso parte dal fatto che se non si conosce il centro della pizza è praticamente impossibile dividerla in due parti uguali. E, invece, è possibile: basta considerare un punto qualsiasi all'interno della pizza e poi tagliarla con 4 tagli che passino per quel punto e formino tra loro un angolo di 45°, come mostra la Fig. 1
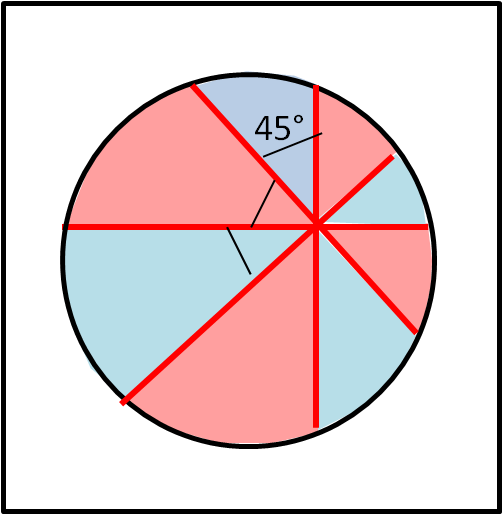
Eseguita questa operazione uno dei due commensali prende le fette pari (rosse) e l'altro le fette dispari (blu). Si può dimostrare, infatti, che la somma delle aree rosse è uguale alla somma delle aree blu. La dimostrazione non è, però, banale e può essere ottenuta attraverso il calcolo integrale, ma anche per via puramente geometrica. L'ultima dimostrazione è stata presentata senza parole, mostrando la pizza separata in tanti piccole parti in modo tale che sommandole opportunamente si ottiene la tesi. Riporto questa soluzione in Fig. 2 e potete divertirvi a dimostrare l'uguaglianza delle parti contrassegnate dalla stessa cifra.
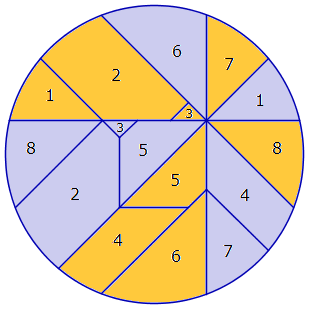
Per ottenere questa intrigante divisione in fette disuguali, ma con somma delle aree uguali, sono però necessari un goniometro e una riga.
Tuttavia, dato che si è voluto evidenziare il risvolto pratico del problema (tagliare in due una pizza), io suggerirei un altro metodo che sembra ancora più pratico e rapido (e che non abbisogna del goniometro). Basta tracciare una corda qualsiasi del cerchio (e segnare i due punti di intersezione con la circonferenza). Poi tracciare una corda parallela a questa, che stia nell'altra metà della pizza (in modo anche occhiometrico) e unire tra loro le estremità delle due corde, come mostra la Fig. 3.
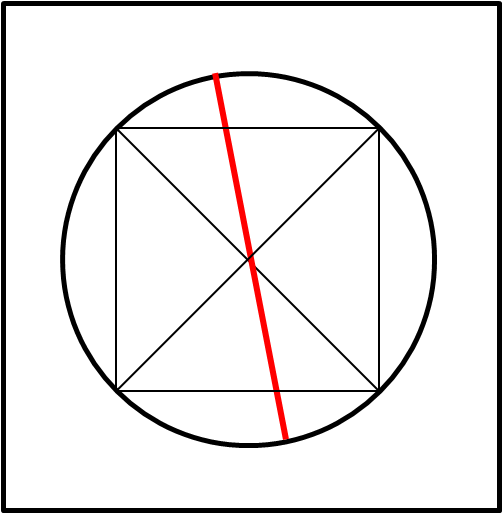
L'intersezione delle due corde indica esattamente il centro del cerchio e, di conseguenza, qualsiasi taglio che passi per esso divide la pizza a metà. Inoltre, non si manifestano problemi relativi alla quantità di crosta che tocca ai due commensali.
Il teorema della pizza è sicuramente molto bello, ma non sembra portare alla soluzione più pratica e veloce... che ne dite?
9 commenti
In modo occhiometrico riesco a tagliarla a metà d'un sol colpo prima che si raffreddi
A Cuneo facciamo in questo modo ...
Se la pizza non è troppo grande, diciamo non oltre 30 - 35 cm di diametro, usiamo un foglio formato A4: appoggiamo un angolo ( A ) sul bordo, poi marchiamo sulla circonferenza i due punti ( B e C )
infine chiediamo ad Alberto di fare velocemente il taglio BC.
Altrimenti chiediamo al pizzaiolo di fare due pizze uguali
Scusate, ma avevo lasciato il computer incustodito e Oreste se ne è approfittato per usare la mia utenza.
(Si è tradito da solo con il riferimento a Cuneo)
Il metodo che utilizziamo su Papalla è questo...
(ed è molto comodo non solo per trovare il centro della pizza del quale, francamente, ci importa poco, bensì per fare mangiare la pizza ai papallini evitando che si rovescino addosso il condimento
)
Così abbiamo diviso la pizza in due metà, in quattro quarti e abbiamo pure trovato il centro! Insomma, abbiamo preso tre piccioni con una pizza. E dico poco!
N.B. Ho evidenziato il centro per il sciur Pautasso, che potrebbe avere problemi ad identificarlo
Ma il metodo del sciur Bernardi/Pautasso mi sembra migliore di quello papalliano perché si presta ad essere usato anche per torte e altre pietanze non pieghevoli
Ringrazio per la segnalazione, però non vedo la scritta "voi siete qui" che faciliterebbe l'orientamento.
Aggiungo (per i meno "rozzi") che la corda c che sottende un angolo alla circonferenza di 90° è proprio un diametro. Diamo un po' di serietà all'ottimo metodo pautassiano...
. Quello papalliano implica un piegamento e un terribile miscuglio di sugo. Lo vedrei meglio per una focaccia ligure o per una bella farinata (cecina...).
Caro sciur Pautasso,
come Lei ben sa, la scritta "Voi siete qui" potrebbe violare la praivasi...
http://www.infinitoteatrodelcosmo.it/2017/06/09/voi-siete-qui/
Recenti dichiarazioni di eminenti giuristi ( di cui non posso fare il nome proprio per motivi di praivasi) sostengono la tesi che la violazione della praivasi si verificherebbe solo se la scritta dicesse "TU sei qui".
Infatti, dicendo genericamente voi siete qui non ci si rivolge ad un soggetto preciso ma una collettività indefinita all'interno della quale non è possibile risalire al singolo individuo.