(Q) Cerchiamo il quadrato (NEW: senza piegamento)*
Attraverso cinque quadrati uguali è facile ottenere una bella croce.
Immaginiamo di averla disegnata in un foglio e di averla ritagliata. A questo punto, vi chiedo:
Qual è il minor numero di tagli rettilinei che devo eseguire per poter arrangiare TUTTI i pezzi ottenuti e costruire un quadrato, senza piegare il foglio
A voi la soluzione!
QUI la soluzione
14 commenti
Per fare i tagli direi di aspettare Alberto che mi sembra il più pratico di queste cose.
Nella attesa, osservo che se ciascuno dei cinque quadrati ha lato l= 1, l'area totale risulta A = 5
Conseguentemente il lato del quadrato ricostruito con i ritagli deve avere lato L =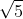
Se il quadrato non deve avere la stessa superficie della croce, si potrebbe fare con due tagli , ottenendo un quadrato e 4 frattaglie (per il gatto), in questo modo:
Oppure il quadrato deve avere la stessa superficie della croce di partenza?
In realtà con due tagli si riesce anche a ottenere il quadrato esattamente della stessa superficie della croce...
Giusta specificazione di Mau: il quadrato deve essere composto da TUTTI i pezzi ottenuti con i tagli.
questa è la figura con i due tagli:
Chissà mai che ne basti uno ?
Piccola integrazione alla figura...
Le linee di taglio sono scelte lungo l'ipotenusa del triangolo rettangolo che ha cateti di lunghezza 1 e 1/2 (segnati nel quadratino in basso della prima immagine)
Questa ipotenusa ha quindi lunghezza pari a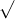
(1+1/4) = 1/2 * 
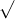5 .
Come si nota nella ultima immagine il lato del quadrato ricomposto è dato da due ipotenuse contigue, quindi è lungo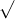
5 , come pronosticato da Oreste nel suo primo commento.
Non avevo letto la raccomandazione di lasciar passare un paio di giorni...
Abbiate pazienza con un povero vecchio.
Il caro Mau, non ha ancora risolto il quiz, ma ha aperto la strada a un teorema che affronteremo tra non molto e che si allaccia a quell'arte meravigliosa che è l'origami.
Infatti: qualsiasi poligono con lati rettilinei può essere ottenuto partendo da un foglio di carta rettangolare attraverso UN SOLO TAGLIO.
Ho cambiato un poco il quiz in modo che sia chiaro che NON si può piegare il foglio di carta... In tal modo, il quiz è ancora aperto!
Coltello giusto... taglio giusto ! (Adesso Enzo dirà che non vale)
cerchi di essere serio sig. Oreste
Caro Oreste, invece della "quadrighigliottina" basterebbe una forbice con cui fare un taglio unico, se solo fosse possibile fare qualche piccola piega... Ma è vietato.
Comunque... zac e zac, con due tagli di forbice si può fare in quattro la croce e il gioco è fatto. Insisti.
Giusto per curiosità, le tre pieghe "vietate" sono queste.
Eseguendole nell'ordine si vengono a sovrapporre i quattro bracci della croce in modo che le 4 linee di taglio coincidono.
Un utile indizio :
Uno dei pezzi che si ottengono tagliando la croce ha la forma di un trapezio.
La base maggiore e l'altezza hanno la stessa misura, quella del lato di uno dei 5 quadrati che formano la croce.
La base minore è metà di quella maggiore.