Categorie: Matematica Riflessioni
Tags: codice segreto fermat
Scritto da: Vincenzo Zappalà
Commenti:7
(Q,I) Risolto il mistero di Fermat ? ****
L'ultimo teorema di Fermat nasconde ancora un mistero irrisolto: era stato realmente risolto da chi l'aveva enunciato oppure no? Oggi, sembra che Fermat non avesse i mezzi e le conoscenze per poterlo dimostrare, ma lui scrive chiaramente: "È impossibile separare un cubo in due cubi, o una potenza quarta in due potenze quarte, o in generale, tutte le potenze maggiori di 2 come somma della stessa potenza. Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina".
Il nostro amico Pippo, però, ha passato anni per cercare un qualche riscontro scritto della dimostrazione e, alla fine, sembra esserci riuscito. Sembrerebbe, infatti, che Fermat avesse scritto la sua autobiografia che conteneva anche la tanto ricercata dimostrazione. Il manoscritto è conservato in un luogo apparentemente impenetrabile, protetto da una combinazione di tre codici numerici, composto da numeri interi, compresi tra 0 e 9.
Pippo è riuscito, non si sa come, ha ottenere i primi due, ma non il terzo, il decisivo per svelare il mistero. Decide comunque di tentare lo stesso e si presenta davanti alla porta. I tre codici da inserire per svelare il mistero occupano rispettivamente 4 , 7 e 10 spazi. Pippo inserisce le prime due che sono:
1210
e
3211000
Resta, adesso, il terzo codice da inserire nei 10 spazi corrispondenti.

Conosciamo bene Pippo e sappiamo quanto sia bravo, ma questa volta ci stupisce veramente! Ci riflette un po' sopra e poi ha il lampo di genio. Pochi minuti di riflessione ed ecco che ricava il terzo codice e la porta si apre... Il manoscritto c'è davvero e ... no, no, non posso certo essere io a svelare un mistero protrattosi per secoli. Anzi, dovrete essere voi a dirmi :
Qual è il codice che ha inserito Pippo ?
Aiuto supplementare: Esiste un solo codice che soddisfi le dieci caselle da riempire
QUI la soluzione






7 commenti
I codici sembrano seguire una logica basata su somme, prodotti e posizioni. Mi spiego meglio: ovvero
ovvero 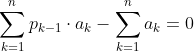
 la posizione occupata dalla singola cifra
la posizione occupata dalla singola cifra 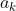
nel primo numero di 4 cifre 1210 la somma delle singole cifre fa 4 → 1+2+1+0=4.
Inoltre, partendo da sinistra verso destra ed assegnando la posizione occupata p (facendola partire da indice 0) da ogni singola cifra, si ha:
p0 ← 1 = a1
p1 ← 2 = a2
p2 ← 1 = a3
p3 ← 0 = a4
mentre la somma dei prodotti delle singole cifre con le rispettive posizioni fa 0×1 + 1×2 + 2×1 + 3×0 = 4
Sembra anche che l’indice della posizione indichi la ripetizione del numero di cifre componenti il codice, nel senso che lo stesso è composta da 1 numero 0, 2 numeri 1, 1 numero 2 e 0 numeri 3.
In generale, pare seguire la regola
con n numero di cifre e
Per sperimentare, ho fatto un ragionamento spicciolo: dato il numero di cifre n, lo divido per 2 e assegno il risultato alla prima cifra a1:
nel caso di n=4 si ha che 4/2 = 2 → a1 = 2 in posizione p0 allora il codice conterrebbe due numeri 0; ma se la prima cifra è 2 la cifra rimanente deve essere per forza 2 affinché la somma delle quattro cifre dia proprio 4;
escludendo che la cifra inizi per zero posso avere:
2200 ma non verifica la condizione perché 0×2 + 1×2 + 2×0 + 3×0 = 2 ≠ 4
2002 idem come sopra 0×2 + 1×0 + 2×0 + 3×0 = 0 ≠ 4
2020 → 0×2 + 1×0 + 2×2 + 3×0 = 4
cioè sia il codice 1210 che 2020 sembrano verificare la condizione
Vado con l’altro codice 3211000, sette cifre che diviso 2 da 3,5 considero la parte intera 3, allora
p0 ← 3 = a1
p1 ← 2 = a2
p2 ← 1 = a3
p3 ← 1 = a4
p4 ← 0 = a5
p5 ← 0 = a6
p6 ← 0 = a7
che significa 3 zeri, due numeri 1, un numero 2, un numero 3 e zero numeri 4,5,6
0×3 + 1×2 + 2×1 + 3×1 + 4×0 + 5×0 + 6×0 = 3+2+1+1+0+0+0 = 7
Per concludere questa analisi iniziale noto che sia nei due codici da 4 cifre che in quello da 7, l’ultima cifra è sempre 0.
Comincio a farmi un'idea sul codice a 10 cifre, ma mi fermo qui per tenere vivo il quiz.
Usando la stessa logica di prima, cerco di determinare il numero che rappresenta l’ultimo codice a 10 cifre. Per rendere il discorso più comprensibile, faccio uso di una tabella dove i numeri sulla prima riga indicano quante volte si ripetono all’interno del codice secondo il rispettivo posto(in verde) collocato nella riga inferiore;

per esempio, nel codice a 4 cifre la tabella esprime le seguenti informazioni:
vi è 1 solo 0 (collocato in posto 3), vi sono 2 numeri 1 (collocati in posto 0 e 2) e vi è un solo 2 (collocato in posto 1). I numeri non sono collocati a caso, ma devono rispettare la regola secondo la quale la somma dei prodotti delle singole cifre con il rispettivo posto sia pari al numero di cifre totali del codice.
Con la stessa logica, si può costruire la tabella per il codice a 7 cifre:

vi sono 3 zeri (collocati in posto 4, 5, 6), 2 numeri 1 (collocati in posto 2 e 3), un numero 2 (collocato in posto 1) e un 3 iniziale (collocato in posto 0); complessivamente 7 cifre singole su 7 posti:
Per il codice a 10 cifre, dato che n=10, divido 10 per 2 e assegno la cifra 5 ottenuta alla posizione iniziale 0; ma dato che la posizione esprime quante ripetizione del proprio indice ci sono nella sequenza di cifre, se alla posizione 0 assegno il 5 significa che il codice conterrà 5 zeri più il 5 assegnato al posto 0, in totale 6 cifre. Ne rimangono da determinare 4 la cui somma deve fare esattamente 5 (5 iniziale + 5 = 10) per rispettare la regola; le quadruple possibili, per quanto detto, non possono contenere zeri perché questi sono già assegnati e occupano 5 posti disponibili su 10: la possibilità restante è allora tre numeri 1 e un numero 2 (1 1 1 2);


devo quindi inserire un 3 nella prima riga seconda colonna (posto 1), un numero 1 nella prima riga terza colonna (posto 2); restano da collocare due numeri 1, ma avrei 5+3+1+1+1=11 che infrange la regola
Provo allora ad aumentare la cifra iniziale portandola a 6: avrei il 6 in posto 0 più sei zeri, in totale 7 cifre. Per quanto detto, la tripla possibile rimanente deve totalizzare 4, quindi rimane solo la possibilità due numeri 1 e un numero 2 (1 1 2). Colloco il 6 in posto 0, il 2 in posto 1, un primo 1 in posto 2, faccio la somma dei prodotti posto×singola cifra: 0×6 + 1×2 + 2×1 = 4, allora l’unica collocazione possibile per il secondo 1 è posto 6:
E siccome è specificato nel problema che "Esiste un solo codice che soddisfi le dieci caselle da riempire" questa è l'unica soluzione.
Cari amici, adesso vi è chiaro perché le banche vi dicono di cambiare le password "frequentemente" ?
Se ci sono in giro tipi come Andy vi converrà cambiarle ogni mattina !
Ma no caro Maurizio,
basta una bella password con 16 simboli alfanumerici, inclusi segni di punteggiatura, caratteri speciali, lettere dell'alfabeto greco antico (maiuscole e minuscole), un contorno di caratteri cirillici, un pizzico di ideogrammi giapponesi, una spruzzata di geroglifici egizi, mezzo bicchiere di caratteri cuneiformi sumeri, una spolveratina di simboli dell'alfabeto sanscrito e....il piatto è servito!!
Semplice, no?!....
Guarda, Andy, io faccio proprio come hai detto tu , ma non sono tranquillo lo stesso.
L'unica cosa che mi calma un po' è la riflessione che di solito ci sono margini di incertezza anche per gli scassinatori di casseforti.
Per esempio, giusto per restare agganciati al quiz...
Avendo solo due numeri iniziali per dedurre il terzo, ci sono varie alternative.
Invece di scoprire la geniale soluzione che hai esposte e della quale io condivido totalmente l'impostazione, Pippo avrebbe potuto trovare un modo diverso per passare da 1210 a 3211000 e , applicando il suo criterio non sarebbe entrato in possesso del documento ( a proposito, tu che l'hai visto... è roba buona?)
Tornando a Pippo.... avrebbe potuto pensare in questo modo:
a b c d (intesa come ultima cifra)
primo numero 4 cifre 1 2 1 0
secondo numero 7 cifre 3 2 1 1 0 0 0
deduzione Pippica: = a+b = b =c = ultima+1000
soluzione Pippica: 5 2 1 1 0 0 1 0 0 0
Certamente possibile ma ... sbagliato ! ( dato che deve essere 6210001000 )
A questo punto la cassaforte si inabissa nella piscina infestata da squali e non si può fare un secondo tentativo.
Noterai che la somma delle cifre di Pippo è 10 , ma questo comunque non era richiesto.
Il numero Pippico, ovviamente, non descrive per niente la propria composizione perché:
ci sono davvero 5 ZERI
ma gli UNI sono ben tre invece di 2
il DUE è uno solo e va bene
ma non c'è alcun TRE
il CINQUE c'è ma non si dice
il fantasmatico SETTE non si vede da nessuna parte.
Quanto alla nota finale nel testo del quiz, quella che proclama l'esistenza di una sola soluzione, potrebbe effettivamente insinuare qualche dubbio.
Pippo si potrebbe domandare perché mai il Prof. ce lo dice (e anche noi ce lo chiederemmo se non fosse che abbiamo a disposizione la tua soluzione e comprendiamo il busillis: sarà unico ? non sarà unico, Mah! ).
Quindi Pippo, non avendo questa pulce nell'orecchio, dovrebbe insospettirsi almeno un po' e cercare qualche altra soluzione che gliela insinui (la pulce nell'orecchio) perché è proprio lì che si giustifica l'avvertimento di Enzo.
Comunque, se non hai ancora inserito il numero magico, rifletti e aspetta che gli squali dormano, anche se penso che non rischi niente.
Caro Andy hai fatto proprio una analisi completa e rigorosa.
La prova della unicità è benvenuta e il tuo metodo di verifica potrà essere utilissimo per ragionare anche su altri numeri.
In particolare mi era sfuggita la regola 6 che è fondamentale e mi risolve un problema che avevo con l'autodescrittivo in base 3. Quindi grazie !!!
Comunque nel precedente commento non volevo assolutamente esprimere dubbi sulla correttezza del numero trovato e della sua diretta correlazione con gli altri due. Ne ero più che certo .
Quello che intendevo è che quando dobbiamo completare una sequenza, soprattutto se ci sono solo due dati di partenza, siamo di fronte ad un ventaglio di possibilità,
Il fatto di riscontrare correlazioni in numero elevato tra la struttura del primo indizio e del secondo è certo confortante e fa presupporre che la migliore strategia sia proprio quella di replicare le correlazioni individuate per generare il dato successivo ma non rimuove la possibilità che la soluzione possa essere diversa.
Anche disponendo di una sequenza di dati più lunga che consentisse di testare la nostra ipotesi, potrebbe esistere una alternativa che genera la stessa sequenza per poi discostarsene ad un certo punto.
Un amico matematico mi faceva un esempio banalissimo ma significativo.
"Questa è la sequenza: 2 4 16 256 .... cosa c'è dopo, in base alla regola che ho stabilito ? Potresti pensare il quadrato di 256 e avrebbe senso. Ma ci può anche essere 3 che poi sarà seguito da 9 e da 81 e dal quadrato di 81, se la mia regola è di scrivere progressivamente i numeri naturali dal 2 in poi , seguiti dalla loro seconda potenza, dalla loro quarta potenza, dalla loro ottava potenza e poi ripartire col prossimo numero naturale etc etc."
E' chiaro che era stato disonesto perché non c'erano indizi a sufficienza e in più c'era una pesante spinta verso una soluzione "evidente". Allora gli ho risposto "Se mi avessi detto che dopo il 256 c'era il tre avrei capito."
"No, avresti cominciato chiederti se fosse meglio mettere 3 al quadrato oppure 3 al cubo."