Un quiz che si è mostrato più complicato del previsto. Il solo Leandro ha dato una sintetica risposta...

Per risolvere graficamente e  velocemente il problema del nostro barcaiolo è necessario ricordare che la via più  breve tra due punti è la linea retta. Dobbiamo perciò trasformare il percorso completo del barcaiolo in un percorso rettilineo. Come fare?

Immaginiamo di voler raggiungere da P il punto Q, toccando l'asse delle x, come mostra la Fig. 1.

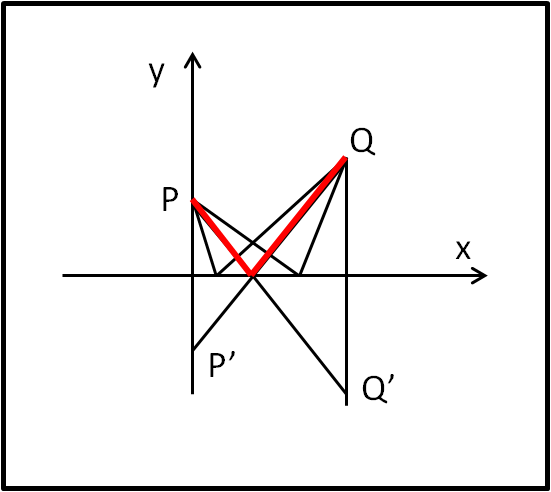
Vi sono infiniti percorsi per ottenere questo risultato, ma ve ne è uno solo che presenta la lunghezza minima. Per visualizzarlo ribaltiamo i punti P e Q rispetto all'asse x, in modo da ottenere i punti P' e Q'. Notiamo subito che per andare da P a Q' la via più breve à la linea retta. Di conseguenza per andare da P a Q, toccando l'asse x, basta combinare i due percorsi, ossia andare da P a R e poi da R a Q. Come si nota questo è anche il percorso che indica la riflessione di un ipotetico raggio luminoso che parta da P e arrivi in Q (il raggio incidente sottende lo stesso angolo di quello riflesso rispetto alla normale in R all'asse x), in accordo con quanto detto da Leandro.

Ma lasciamo stare la riflessione e pensiamo al procedimento più semplice che può fare il barcaiolo. Lui ha una carta topografica del lago e non deve fare altro che riportare il lago  ribaltandolo due volte  come mostra la Fig. 2.

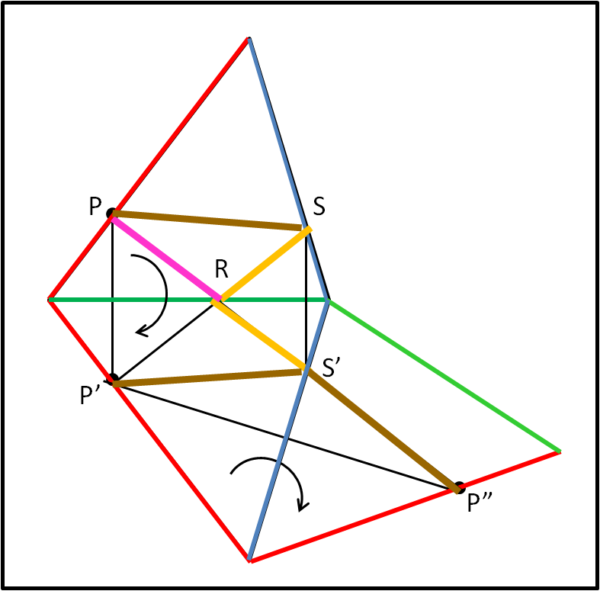
Il suo punto P passa prima in P' e poi in P". Il percorso minimo deve congiungere il punto P con P" secondo una linea retta. In altre parole congiunge il punto P con se stesso dopo due ribaltamenti. Questo tracciato individua subito il punto R in cui tocca il lato verde e il punto S dove tocca il lato blu. RS', infatti, si ribalta in RS. Basta poi congiungere S con P, che risulta essere il segmento S'P" ribaltato prima in S'P' e poi proprio in SP.

Un gioco di semplici ribaltamenti che il barcaiolo può preparare una volta per tutte, conoscendo la sua posizione P. Ovviamente, se cambiasse la posizione P, cambierebbe il percorso minimo e, quindi, i punti R e S.

La procedura funziona anche con un lago "quadrilatero", ma non sempre, dato che nella costruzione non abbiamo imposto realmente che il tracciato tocchi tutti i lati e la procedura potrebbe dare soluzioni che non soddisfano queste condizioni. Nella Fig. 3 mostro un quadrilatero (lago) giallo e un punto P scelto in una posizione conveniente.

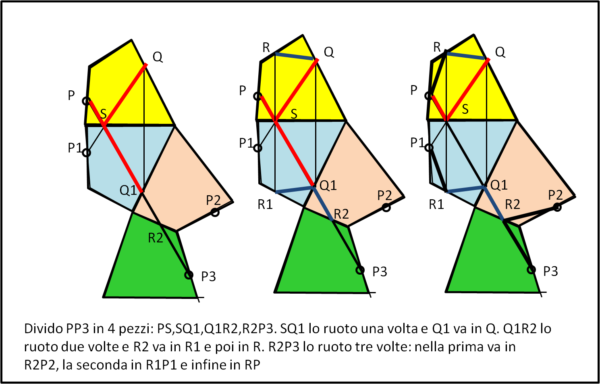
Questa volta i ribaltamenti sono tre, ma la procedura è sempre la stessa...

Cambiando posizione a P o cambiando il quadrilatero (ad esempio un trapezio isoscele) la costruzione non funziona più ...

Chi vuole cercare di generalizzare la procedura anche in questi casi "sfortunati" si accomodi pure. Fortunatamente il nostro lago è triangolare e acutangolo...