Eseguendo una sequenza di rotazioni si ottengono risultati diversi a seconda dell'ordine in cui si succedono le rotazioni. Occorre quindi operare una scelta, non casuale, al fine di ottenere la configurazione adatta al problema da risolvere.

Sequenza di rotazioni

Abbiamo visto nel precedente articolo di Oreste (matrici di rotazione? Sì, grazie) come, applicando le matrici di rotazione al vettore iniziale, opportunamente scelto, si giunga a determinare il vettore finale che fornisce l'orientamento del raggio di sole nella data, ora e luogo di nostro interesse e quindi le relative coordinate, sulla parete verticale, del punto ombra proiettato dallo gnomone.

Dato che le rotazioni da eseguire sono tre,  non abbiamo una sola sequenza, ma  sei possibili  sequenze di rotazioni tra cui scegliere quella coerente con il problema che stiamo studiando.

a.    R^x_-23,45° R^z_30° R^x_45°

b.   R^x_-23,45° R^x_45° R^z_30°

c.   R^z_30° R^x_-23,45° R^x_45°

d.   R^z_30° R^x_45° R^x_-23,45°

e.  R^x_45° R^z_30° R^x_-23,45°

f.   R^x_45° R^x_-23,45° R^z_30°

Ogni sequenza di rotazioni  produce come risultato,  un diverso vettore finale.

La sequenza utilizzata (a) R^x_-23,45° R^z_30° R^x_45° ha fornito il risultato desiderato, ma in base a quale

ragionamento sono state scartate le altre sequenze?

La risposta non si trova neppure nel testo di Tasselli, dove si dice:

"Sarà facile ora, con successive rotazioni attorno agli assi principali, posizionare il vettore nella giusta direzione. Le rotazioni devono essere impartite con un ordine ben preciso come se giocassimo con il cubo di Rubik affinché la rotazione del vettore attorno all’asse polare venga correttamente scomposta in semplici rotazioni attorno agli assi principali."

Procediamo per esclusione valutando cosa succede anteponendo una rotazione alle altre.

1.  la rotazione R^z_30° non può essere la prima perché il vettore iniziale (0,-1,0) ruoterebbe restando sul piano XY e non  sarebbe più possibile generare il cono d'ombra con vertice nella punta dello stilo e asse coincidente con Z. Quindi questa rotazione può essere solo la seconda o la terza.

Per comprendere a fondo questa osservazione osserviamo la figura 1...

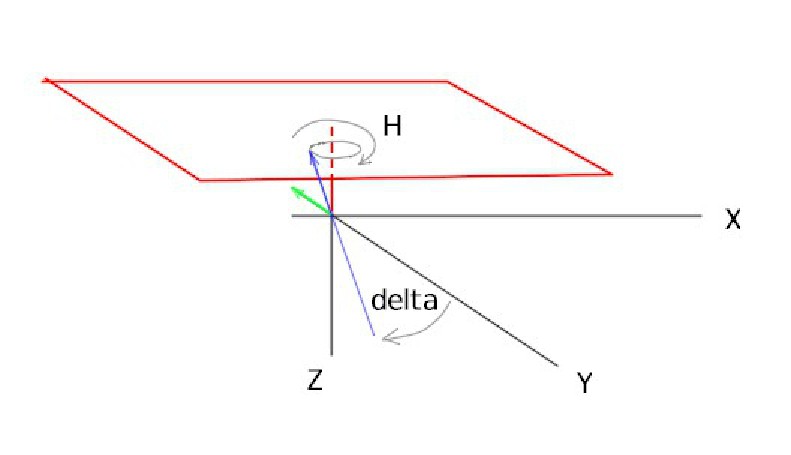Iniziando la sequenza con la rotazione (delta) del vettore iniziale (verde) attorno all'asse x, esso si trasforma nel vettore blu. Con la successiva rotazione attorno all'asse Z questo vettore blu genera una superficie conica con vertice nella punta dello stilo e asse Z. Il cono è l'insieme dei prolungamenti di tutti i raggi di sole (ossia le proiezioni dell'ombra) nell'arco delle 24 ore, da cui il termine “cono d'ombra”. Questa situazione rispecchia esattamente quanto avviene nella realtà.

E confrontiamola con la situazione che si crea nella figura 2 …

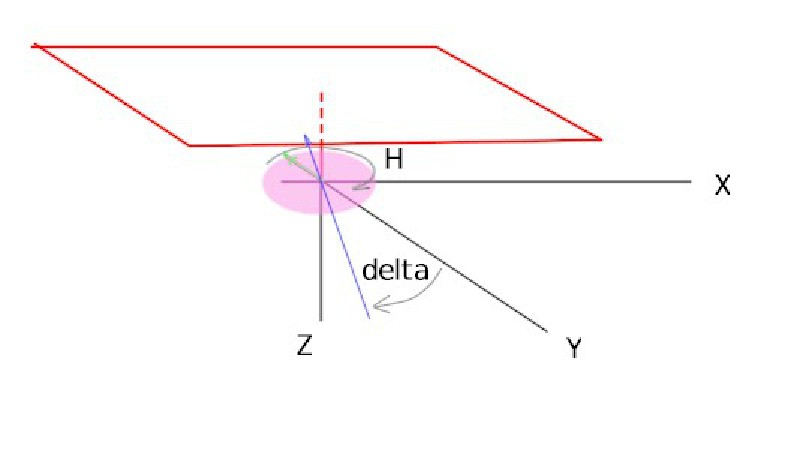In questo caso la prima rotazione avviene attorno all'asse Z. Il vettore verde (iniziale) si muove sul piano XY descrivendo una traiettoria circolare, un settore di circonferenza proporzionale ad H. La rotazione successiva, di angolo delta attorno all'asse X, ruota semplicemente il piano della circonferenza senza generare alcun cono d'ombra. E' quindi evidente che iniziare la sequenza con la rotazione attorno a Z non porta al risultato corretto.

In base a questi ragionamenti possiamo escludere due delle 6 sequenze, precisamente la (c) e la (d)

Proseguiamo ora con la ricerca di motivi di esclusione per le altre sequenze

2. La rotazione R^x_45° non può precedere le altre rotazioni _.Se precedesse la rotazione (delta) attorno all'asse X risulterebbe poi alterata l'apertura del cono d'ombra. Ma ciò avverrebbe anche se precedesse solo la rotazione (H) attorno a Z.Quindi questa rotazione può essere solo l'ultima della sequenza.

Con questa seconda osservazione possiamo escludere tre sequenze delle quattro che erano rimaste, precisamente la (b), la (e) e la (f)

Resta valida solo la sequenza (a), che è proprio quella con cui siamo giunti al risultato.