Questo articolo è stato inserito nella pagina d'archivio dedicata all'Astronomia Classica

 

Le meridiane che vediamo in molti borghi italiani, o anche in altri paesi europei, possono indurci a pensare che, ovunque sia, una meridiana deve avere un simile aspetto. Non è proprio così.  Una meridiana realizzata all'Equatore potrebbe apparirvi piuttosto strana. Ma la cosa interessante è che la potrete usare a qualsiasi latitudine e longitudine.

 

Una meridiana per l'Equatore e non solo 

Le meridiane che vediamo in molti borghi italiani, o anche in altri paesi europei, possono indurci a pensare che, ovunque sia, una meridiana deve avere un simile aspetto. Non è proprio così.  Una meridiana realizzata per l'Equatore potrebbe apparirvi piuttosto strana. Ma la cosa interessante è che la potrete usare a qualsiasi latitudine e longitudine.

 

Alcune osservazioni preliminari

Diecimila chilometri a sud di Milano, seguendo il meridiano, si arriva a Port-Gentil, nel Gabon. Precisamente in un tratto di litorale rivolto verso nord, a un tiro di schioppo dall'Equatore.

Il posto non è male, come vedete.

Ma non siamo qui per prendere il sole, bensì per osservarlo. Quindi spostiamoci con il nostro tavolino in un luogo appartato, sulla riva, e stando sul lato Sud, guardiamo verso Nord..

Per prima cosa fissiamo uno stilo verticale sul ripiano. Poi, ogni 10 minuti, segniamo l'ombra della sua punta collegando via via i segni per tracciare la linea disegnata dai raggi del sole.

Oggi è il giorno dell'equinozio primaverile. Qui sopra vediamo cosa appare sotto i nostri occhi nelle prime ore del pomeriggio.

Dato che i raggi solari durante questo giorno sono tutti adagiati sul piano perpendicolare al piano del tavolo, l'ombra della punta dello stilo disegnerà una retta orientata esattamente da Ovest ad Est, passante per la base dello stilo della nostra meridiana per l'Equatore.

Si tratta della retta Equinoziale.

Ripetendo l'osservazione a distanza di sei mesi, all'equinozio di autunno, otterremmo la stessa linea.

In tutti i giorni compresi tra un equinozio e l'altro non vedremo mai una linea retta ma una curva.

Questo è dovuto al fatto che i raggi non saranno più su un piano ma su una superficie curva.

Tra l'inizio della primavera e l'autunno la curva appare convessa e si trova sotto la linea equinoziale. Il sole si sposta progressivamente verso Nord fino al solstizio estivo e poi ritorna, nei mesi successivi, alla posizione che aveva all'equinozio.

La curva più lontana dalla equinoziale, la vediamo il 21 giugno, solstizio di' estate.

Nei giorni che vanno dall'inizio dell'autunno alla primavera vediamo invece delle curve concave situate al di sopra della equinoziale. Il sole si sposta progressivamente verso Sud fino al solstizio invernale e poi si riporta verso la posizione che aveva all'equinozio.

In questi giorni la curva più accentuata e distante dalla equinoziale, la possiamo vedere il 21 dicembre, giorno del solstizio d'inverno.

Il Sole visto dalla punta dello stilo

Dalla sommità dello stilo  della meridiana per l'Equatore si vedono giungere i raggi del Sole. Di minuto in minuto il raggio arriva da una direzione diversa dato che il Sole si muove lungo una traiettoria circolare dall'alba al tramonto (che all'equatore si verificano alle 6 e alle 18).

Questo arco di circonferenza “diurno”, nei giorni degli equinozi passa esattamente a Est e ad Ovest e a mezzogiorno il Sole si troverà esattamente allo Zenit.

Tutti i raggi si dispongono sul piano individuato dalla linea Est Ovest e dallo stilo, un piano perpendicolare a quello del tavolo.

L'ombra della punta dello stilo si troverà costantemente sulla linea di intersezione tra questi due piani, percorrendo la linea Equinoziale.

Nel giorno successivo all'equinozio di primavera, il Sole sorgerà in un punto leggermente più a Nord, sempre alle ore 6. Percorrerà in cielo un arco spostato più a Nord e a mezzogiorno non lo vedremo esattamente allo Zenit, ma traslato verso Nord.

Questo spostamento, visto dalla punta dello stilo della meridiana per l'Equatore, causa la perdita di complanarità dello stilo con tutti i raggi provenienti dal Sole durante la giornata. La superficie di questi raggi non sarà più un piano ma un cono avente come base la traiettoria del Sole e come vertice, rivolto a Sud, la punta dello stilo.

L'asse di questo cono, orientato nella direzione Nord Sud, risulterà parallelo al piano del tavolo. Il suo angolo di apertura è molto ampio e lo scostamento della superficie conica dal piano non è altro che l'angolo di declinazione solare che varia quotidianamente. In realtà questo angolo varia istante per istante, ma lo consideriamo costante durante tutto il giorno.

Simmetrie

Lo stesso spostamento appena descritto si verifica in modo del tutto simmetrico all'equinozio d'autunno.

Questa volta l'arco diurno si sposterà verso Sud e la raggiera delle generatrici costituirà un cono con il vertice che punta verso Nord.

La specularità che abbiamo riscontrato, ci consente di limitare l'analisi a metà dell'anno e utilizzare il risultato grafico che otterremo anche per l'altra metà.

Esiste un'ulteriore simmetria speculare che si può notare durante la giornata. Essa dipende dal fatto che la direzione Est – Ovest della linea equinoziale è perpendicolare alla direzione Nord -Sud lungo la quale si dispone ogni giorno l'ombra dello stilo al mezzogiorno. E' la direzione della linea Meridiana.

Il raggio solare, un'ora prima delle 12, proietterà l'ombra della punta dello stilo verso Ovest ad una certa distanza dalla linea Meridiana. Un'ora dopo le 12 l'ombra cadrà alla medesima distanza dalla linea Meridiana dalla parte opposta, verso Est.

La specularità rispetto alla linea meridiana, che si aggiunge alla specularità rispetto alla linea equinoziale, ci consente di restringere il campo di analisi, dimezzando ulteriormente il problema.

In conclusione sarà sufficiente studiare un quarto dell'intero quadrante, ovvero le curve tra un solstizio ed un equinozio, limitatamente alle ore dall'alba alle 12 ( ovvero dalle 12 al tramonto).

Questa semplificazione è possibile grazie alla particolare posizione equatoriale in cui ci troviamo.

Oltre lo stilo

Abbiamo visto che i raggi del Sole, convergenti sulla punta dello stilo, durante il giorno, generano la superficie di un cono.

Ma cosa succede oltre lo stilo?

Mentre i raggi che lo colpiscono vengono interrotti nel loro cammino, i raggi circostanti (paralleli) proseguono senza ostacoli fino ad incontrare, illuminandolo, il piano del tavolo.

Noteremo allora la mancanza della luce dei raggi bloccati dallo stilo, cioè la sua ombra.

Nel loro insieme tutti i raggi del cono di luce bloccati generano, oltre la punta dello stilo, un cono speculare di ombra.

Il percorso della sorgente luminosa (Sole) lungo l'arco di circonferenza diurno avviene in senso antiorario (dal nostro punto di vista rivolto verso Nord) e contemporaneamente il punto ombra ruota sulla base circolare del proprio cono in senso opposto, orario.

Dopo l'equinozio di marzo, giorno in cui è nulla la declinazione solare, il cono di luce e quello di ombra sono molto appiattiti. In seguito il cono presenterà una apertura che va riducendosi dato che al crescere della declinazione solare la superficie conica si allontana sempre di più dal piano equinoziale.

Nel giorno del solstizio di giugno la declinazione tocca il suo massimo di 23,45° e l'apertura del cono varrà 90° - 23,45° = 66,55°

Le proiezioni del cono d'ombra

L'intersezione della superficie del cono con il piano del tavolo, a cui l'asse del cono è parallelo, ha esattamente la forma di una iperbole.

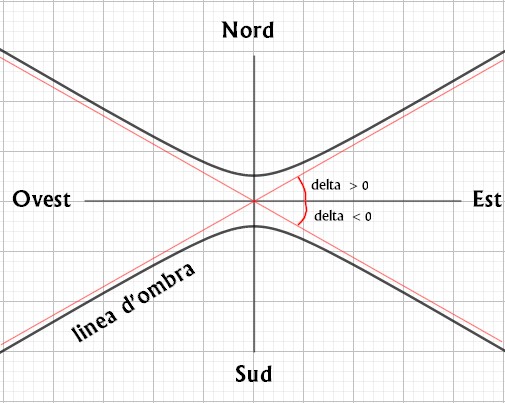
Questa curva è composta da due rami simmetrici. Al solstizio estivo il valore di “delta” è positivo e l'ombra segue il ramo inferiore. Viceversa, al solstizio invernale, essendo “delta” negativo, segue il ramo superiore.

Rappresentiamo in proiezioni ortogonali sui tre piani del sistema di riferimento (PL laterale, PF frontale e PO orizzontale) materializzato dal piano del tavolo e dalla verticale passante per il suo vertice Nord – Ovest, l'intersezione tra cono d'ombra e piano del tavolo.

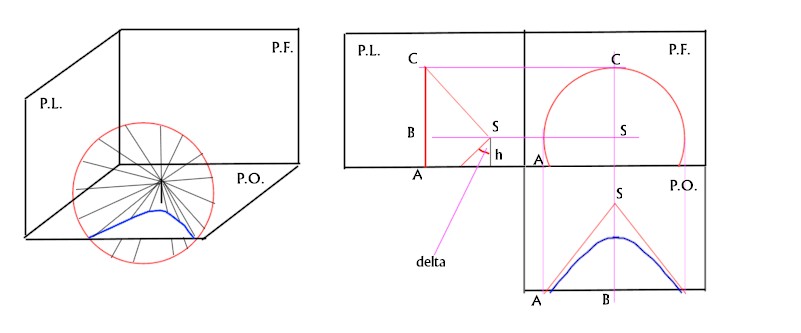
Il punto S è il vertice del cono e corrisponde alla punta dello stilo, la cui altezza è “h”.

Avendo troncato il cono alla distanza BS dal vertice, il raggio della sua base è rappresentato da CB. La quota del punto C è quindi data da CB + h.

Passiamo al piano cartesiano

Assumiamo come coordinate dell'origine la base dello stilo nella vista frontale.

Le sue coordinate sono quindi X=0 e Z = 0 .

Il raggio “r” dal centro S della circonferenza al generico punto P (che ha coordinate P(x,z), è esprimibile con il Teorema di Pitagora applicato al triangolo rettangolo SQP

r² = SQ² + PQ² = x² + (z – h)²

Se guardiamo la proiezione sulla parete orizzontale. Potremo valutare la relazione tra il raggio e la coordinata “y”.

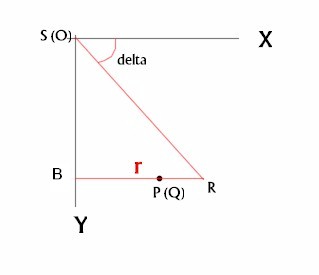
Le coordinate di P su questo piano sono P(x,y)

La nostra attenzione, tuttavia, non va ora al punto P, ma al punto R che fino ad ora non avevamo considerato.

Nel triangolo rettangolo SBR vediamo una relazione tra il raggio ed il valore della coordinata Y, attraverso il valore della tangente dell'angolo “delta” della declinazione solare.

y = r tan (delta)

quadrando abbiamo r² = y² / tan² (delta)

Sezioniamo il cono

Abbiamo appena trovato una seconda espressione per r² .

Possiamo equipararla con la prima:

y² / tan² (delta) = x² + (z – h)²

Questa uguaglianza lega tutte e tre le coordinate X,Y,Z per tutti i punti appartenenti alla superficie del cono. Si tratta proprio della equazione della nostra superficie conica.

Per sezionarla con il piano orizzontale del tavolo dobbiamo esprimere la relazione che descrive quel piano, che afferma semplicemente che tutti i suoi punti devono avere quota nulla:

z = 0

La linea di intersezione si ottiene collegando le due equazioni in un sistema.

Dato che z deve essere nulla, andiamo ad inserire questo valore nella equazione del cono

y² = tan² (delta)*(x² + (z – h)² ) otteniamo:

y² = tan² (delta)*(x² + ( – h)² )

y² = tan² (delta)*(x² + h² ) da cui:

y = ± tan(delta) √( x² + h² )

Ecco così trovata l'equazione della iperbole che potremo disegnare punto per punto, conoscendo la declinazione delta in quel particolare giorno,

Troveremo contemporaneamente i due valori di y, positivo e negativo, cosa che ci ricorda la simmetria riscontrata.

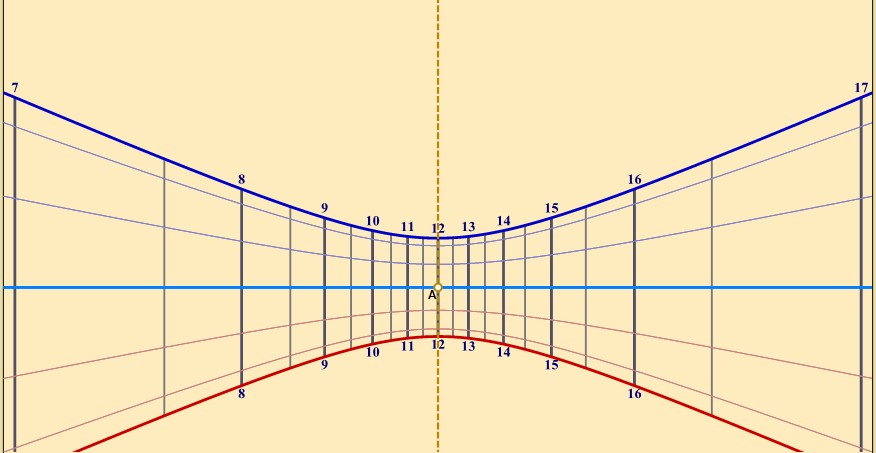
Variando il valore di delta (0° all'equinozio, 11° a trenta giorni di distanza, 20° al sessantesimo giorno e 23,45° al solstizio), potremo tracciare la retta equinoziale e tre iperboli che saranno valide anche nei tre mesi che seguono il solstizio dato che entreranno in gioco “a ritroso”, mese dopo mese fino a tornare sulla retta equinoziale.

Ribaltando il disegno ottenuto avremo, per simmetria, le iperboli  della meridiana per l'Equatore degli altri 6 mesi.

Le rette orarie

Abbiamo finalmente il tracciato delle iperboli diurne per ciascun mese a partire da marzo.

Per completare la rete delle curve che costituiscono la meridiana per l'equatore ci mancano ancora le rette che indicano le ore del giorno.

Tutte queste rette convergono in un punto preciso sul piano del quadrante, esattamente dove esso viene colpito dal prolungamento della retta che congiunge la punta dello stilo alla stella polare.

In altre parole, questa retta è la parallela all'asse terrestre che passa per la punta dello stilo.

Ma nel nostro caso specifico, questa retta risulterà parallela al piano del quadrante e perpendicolare alla linea equinoziale.

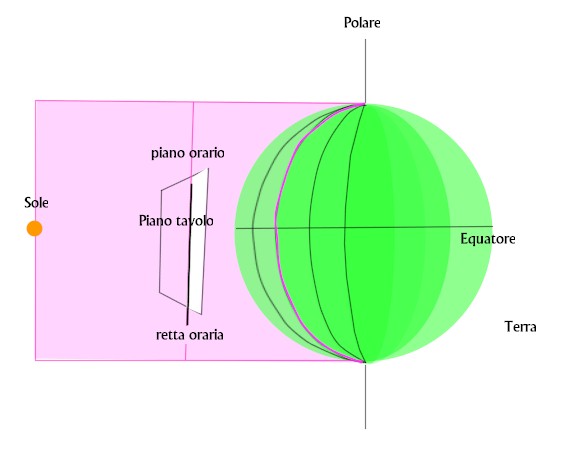
Le rette orarie, quindi, risulteranno tutte parallele ed opportunamente spaziate tra loro in funzione della inclinazione dei raggi solari per ciascuna ora del giorno..

La costruzione geometrica risulta assai semplice.

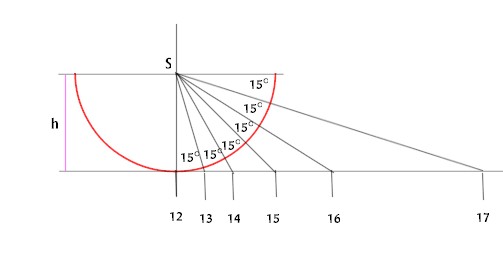
La vediamo accennata nella figura qui sopra per le ore pomeridiane.

Si tratta di intercettare sulla linea equinoziale le linee di proiezione dal punto S, spaziate di 15° (corrispondenti all'angolo di rotazione della Terra in un'ora ) e poi congiungere i punti trovati al punto proiettato dal polo ( nel nostro caso all'infinito).

Queste sono le spaziature da utilizzare per le rette orarie che completano il reticolo.

Ora che abbiamo il tracciato valido per la meridiana per l'equatore vi chiederete “ Sì, va bene, ma quanti di noi e per quanto tempo avranno modo di trovarsi all'equatore, su quella bella spiaggia, e quindi poter utilizzare questa meridiana?”

 

La trasportabilità

Ebbene, non è detto che una meridiana orizzontale, progettata per una certa latitudine, non possa essere utilizzata in una località diversa.

La meridiana per l'equatore, se verrà portata ad una diversa latitudine, sarà posata su un piano orizzontale locale che ha una inclinazione (pari alla stessa latitudine) rispetto al piano locale dell'equatore. Quindi se ora la incliniamo in modo da compensare questo angolo, tornerà automaticamente a vedere il sole “come se fosse all'equatore”. Il suo quadrante risulterà parallelo all'asse terrestre.

E la potremo utilizzare anche nel luogo in cui ci troviamo.

Per quanto riguarda la longitudine, personalmente non vedo problemi, dato che la longitudine di Port-Gentil in Gabon è la medesima di Milano, Genova e Cagliari, che sono i luoghi che frequento durante l'anno.  In ogni caso lo scostamento dal centro del fuso orario comporta l'aggiunta di 24 minuti, cosa che mi è ben nota.

Mi rendo conto però che per molti lettori la situazione può essere diversa.

Per loro vale comunque il consueto ragionamento basato sulla distanza tra il meridiano locale ed il meridiano centrale del fuso orario di riferimento.

In Italia corrisponde al meridiano che si trova a 15° da Greenwich, ma la procedura da seguire è la medesima per qualsiasi punto del pianeta.

Se vi trovate sul meridiano di riferimento, allora il mezzogiorno locale corrisponderà alle ore 12 degli orologi (salvo la ulteriore correzione della equazione del tempo) A seconda che siate  ad Est del meridiano oppure ad Ovest, dovrete considerare che ogni grado di scostamento comporta 4 minuti di ritardo (se siamo più a Ovest) ovvero 4 minuti di anticipo (se siamo più a Est).

 Nel caso che la meridiana sia in anticipo di un certo numero di minuti dovrete sottrarli alla lettura per avere l'ora civile. Se, al contrario, è in ritardo, dovrete sommarli.

Per chi non ricordasse o non sapesse come funziona l'equazione del tempo, è sempre possibile consultare l'articolo di Oreste a questo link.