Va bene, ho capito... i quiz facili non attirano nessuno ed eviterò di proporli. Mi limiterò a quelli un po' più complicati che stimolano i più esperti. Tuttavia, certe proprietà della geometria "base" non possono restare sconosciute e nemmeno le piccole strategie adatte alla loro soluzione. Le proporrò, perciò, come descrizioni e non come quiz, sperando che vengano lette e fatte proprie. Anche l'astrofisica più "elevata" (per non dire la matematica e la fisica) ha bisogno di una base geometrica di livello elementare. Non si nasce "imparati" ed è bene salire le scale senza saltare troppi gradini, con rischi di gravi cadute.

Di seguito trovate le proprietà con la loro dimostrazione. Se, poi, nessuno risponde perché sono cose troppo ovvie, chiedo perdono...

Alcune proprietà "segrete" di un triangolo qualsiasi

(1)  Due punti medi

Dato un triangolo qualsiasi ABC, segniamo i punti medi M e N dei lati AB e BC. Il segmento MN è uguale alla metà del lato AC.

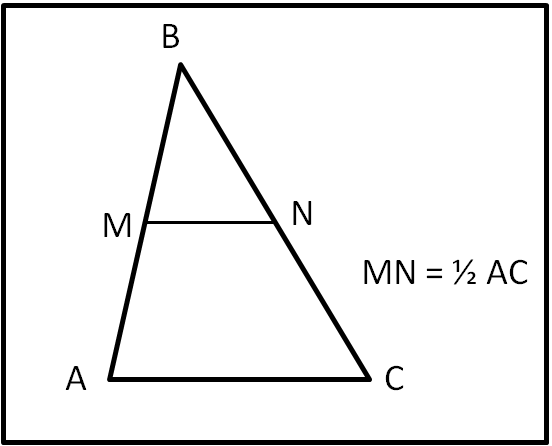
La soluzione è veramente immediata. I due triangoli BMN e BAC sono simili, in quanto hanno un angolo in comune e due lati che stanno tra loro in proporzione costante, ossia BN = 1/2 BC e BM = 1/2 BA (per costruzione). Ne segue che anche i loro restanti lati devono accettare la stessa proporzione, ossia:

MN = 1/2 AC

(2) Mediana

Dato un triangolo qualsiasi ABC se traccio la mediana da A al lato BC ottengo due triangoli, ANC e ANB. I due triangoli hanno la stessa area ed essa vale la metà di quella del triangolo ABC.

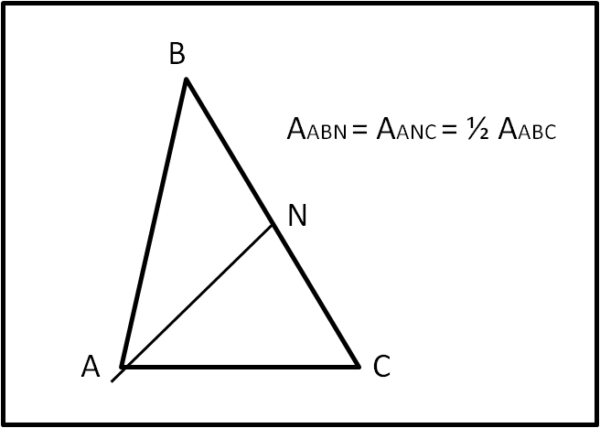
Consideriamo i due triangoli ABN e ANC. Essi hanno la stessa base, dato che BN = NC e la stessa altezza (basta tracciare la perpendicolare da A al lato BC, che vale per entrambi i triangoli). Ne segue che essi hanno la stessa area che è, quindi, la metà dell'area del triangolo ABC.

(3) Baricentro

Dato un triangolo qualsiasi ABC determiniamo il suo baricentro G (intersezione delle tre mediane). Uniamo G con i tre vertici A, B e C. I tre triangoli che si formano hanno la stessa area ed essa vale 1/3 di quella del triangolo ABC.

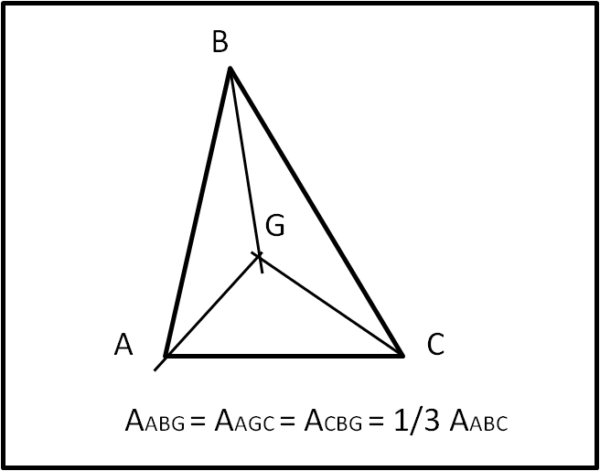
Prolunghiamo le mediane e indichiamo con M,N e K i loro  punti d'incontro con i tre lati (Fig. 3b)

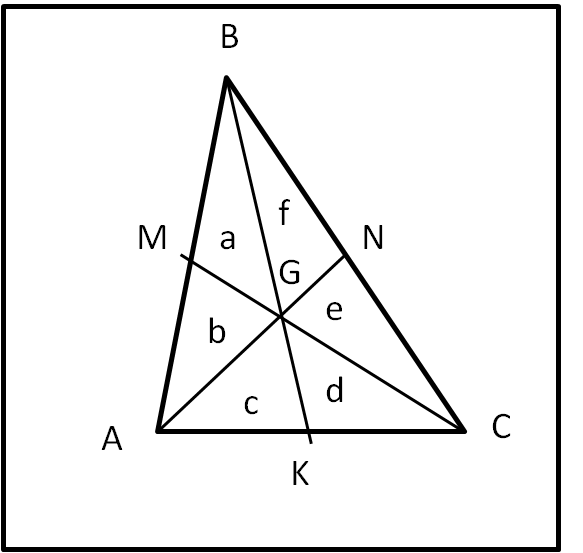
Otteniamo 6 piccoli triangoli di area a, b, c, d, , e ed f. Ma GK, GM e GN sono le mediane dei triangoli ABG, BGC e AGC e quindi:

a = b

c = d                      .... (1)

e = f

BK è la mediano rispetto ad AC del triangolo ABC, per cui divide la sua area in due parti uguali (vedi proprietà precedente). Ne segue che:

areaABK = areaBKC

ossia:

a + b + c = d + e + f

Ricordando le (1) possiamo scrivere

a + a + c = c + e + e

2a = 2e

a = e

e via dicendo...

insomma :

a = b = c = d = e = f

(4) Tre punti medi

Dato un triangolo qualsiasi ABC, se uniamo tra loro i punti medi dei lati otteniamo quattro triangoli congruenti tra loro.

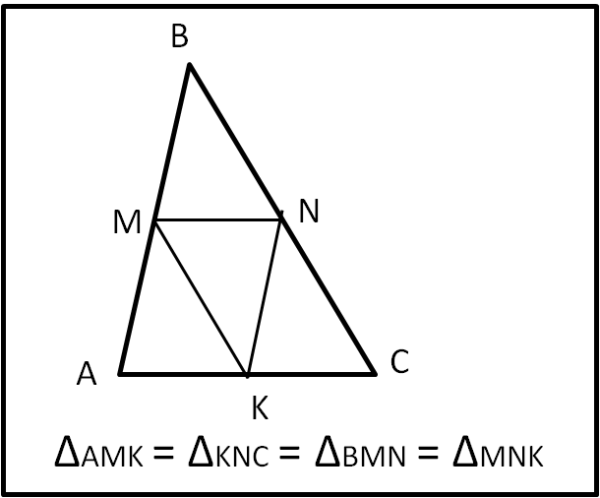
Dalla prima proprietà abbiamo visto che MN = AK = KC, BN = NC = MK e NK = AM = MB. Ne segue che i quattro triangoli sono uguali tra loro (tre lati uguali) e quindi hanno ovviamente la stessa area.

L'uguaglianza delle aree si può avere anche ricordando che i lati di BMN sono la metà di quelli di ABC e, quindi, passando all'area, si ha la proporzionalità di 1/4. Ne segue che ogni triangolo piccolo ha area pari a 1/4 di quella di ABC.