Categorie: Matematica
Tags: geometria perimetro quiz triangolo ottusangolo
Scritto da: Vincenzo Zappalà
Commenti:53
(Q) Un triangolo ottusangolo ****
Proviamo a inserire un quiz dedicato ai più esperti... La soluzione non è in realtà molto difficile, ma abbisogna di un un po' di arguzia e fantasia per non essere costretti a un lungo e monotono approccio. Esso è stato presentato a un concorso internazionale di matematica, dove il tempo -per ogni esercizio- era piuttosto limitato.
Descriviamo il problema...
Consideriamo un triangolo ABC in cui l'angolo in A è ottuso. Le lunghezze dei suoi lati sono numeri interi. In particolare, AB = 100. Sappiamo inoltre che l'angolo in B è uguale a due volte l'angolo in C, di ampiezza θ (sconosciuta).
Determinare il perimetro del triangolo. Non sono ammessi casi degenere, ossia θ non può essere zero.
Per seguire meglio i vostri ragionamenti, inseriamo una figura a cui fare riferimento.
53 commenti
Caro Enzo,
la mia è più che altro una intuizione che però porta a valori coerenti con ciò che viene richiesto,
anche se con l'ausilio della calcolatrice...
https://i.imgur.com/Z30Ro2k.png
caro Andy,
l'inizio è buono, ma poi ti complichi la vita...
confermo 100+180+224 anche con metodo diverso, utilizzando due cerchi intersecati ed il teorema dell'angolo alle circonferenza.
Il cerchio è uno solo centrato in B.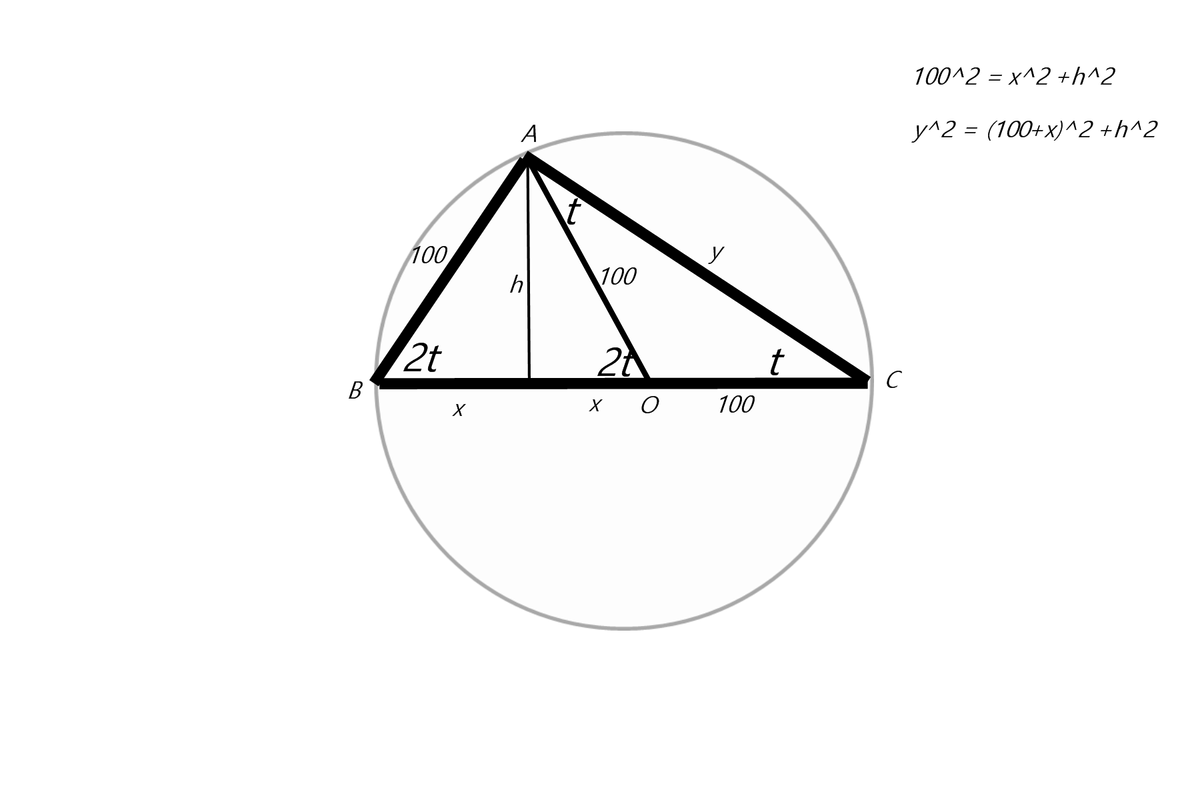
Dalle formule si giunge a
che si può scrivere
Considerando che A è ottuso l'angolo in B deve essere minore di 60 gradi.
La proiezione di 100 sul lato BC deve essere superiore a 100*cos(60) = 50 .
Quindi il quadrato deve essere compreso fra 300 e 400.
L'unico valore intero che al quadrato si pone tra 200 e 300 è 18 (18^2=324).
Quindi y= 18*10 =180 e conseguentemente la proiezione di AB è x = 62 , da cui il lato BC è = a 100+2*62 = 224.
refuso , intedevo un quadrato tra 300 e 400 . Esiste anche 19^2 = 361 ma y è pari e il quadrato di un numero pari è pari.
Scusa Leandro... ma come spesso capita sei troppo sintetico. Dovresti spiegare bene tutta la tua dimostrazione. Dire "formule" è troppo generico e pochi lettori riescono a seguirti. Non interessa tanto il risultato, ma come ci si arriva e il metodo usato è molto importante per vedere le varie strade.
In ogni caso, confermo anch'io che b = 180 è un valore corretto, ma....
Inoltre, il tuo triangolo inscritto nel cerchio impone che l'angolo in A sia 90°, che non torna con l'imposizione che l'angolo sia ottuso
In effetti i cerchi sono due.
1) si traccia il primo cerchio con centro B e raggio AB=100
2) si traccia il secondo cerchio di raggio =100 in modo che i due cerchi si intersechino in A e D
3) l'angolo ABD è angolo al centro del primo cerchio e quindi è il doppio
dell 'angolo alla circonferenza ACD del secondo cerchio.
4) per costruzione AO=HH' =100
5) BAOC è un trapezio rettangolo con basi 100 e 100+2 BH, chiameremo x=BH
6) si tracci l' altezza h da A verso BC
7) ABH è rettangolo, quindi, applicando Pitagora, è valida la prima equazione in alto
9) si sottragga la prima equazione dalla seconda per ottenere con semplici passaggi
Mi scuso per la sinteticità ma Fermat ha fatto di peggio.
Hai proprio ragione Enzo, cercherò di esprimere il ragionamento in maniera più semplice, riportando "in chiaro" le parti salienti del mio precedente post "spoilerato".
Partendo dal fatto che la somma degli angoli interni di un triangolo fa 180° , posso scrivere per il caso in oggetto:
2ϑ+ ϑ + γ = 180° cioè 3ϑ = 180° – γ ; ma se γ > 90°
allora 180° – γ < 90° per cui 3ϑ < 90° → ϑ < 30°&space;=&space;2\cdot&space;cos^2&space;(\vartheta)&space;-&space;1)
;&space;=&space;200&space;\cdot&space;cos^2&space;(\vartheta))
&space;-&space;100&space;+&space;200&space;\cdot&space;cos^2(\vartheta))
&space;-&space;100)
(2)
Per la legge dei seni posso scrivere: 100/sin(ϑ) = b/sin(2ϑ) ;
ma sin(2ϑ) = 2·sin(ϑ)cos(ϑ) per cui l’eguaglianza precedente diventa:
100/sin(ϑ) = b/( 2·sin(ϑ)cos(ϑ) ) ovvero 200·cos(ϑ) = b
Ma siccome b deve essere un numero intero e il valore del coseno di un angolo oscilla tra 0 e 1, allora b deve essere un intero minore di 200 ; a questo punto faccio la congettura che cos(ϑ) = k/D{200} dove D{200} sono i divisori interi di 200: D{200} = {1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200}. e k un intero positivo minore del singolo divisore di 200.
Ma c’è da considerare una altro vincolo: se ϑ < 30° e il coseno di 30 fa √3 / 2 ≈ 87/100 , allora
87/100 ≤ cos(ϑ) < 100/100 .
Il lato a è la somma della proiezioni degli altri due lati su di esso, ovvero
a = 100·cos(2ϑ) + b·cos(ϑ) (1)
ma
e se b = 200·cos(ϑ) allora
sostituendo nella (1) si avrà che
ovvero a =
Provo adesso ad inserire nella (2) i valori di coseno a partire da 87/100 aumentando successivamente di 1 il numeratore
cos(ϑ) a
87/100 202,76
88/100 209,76
89/100 216,84
90/100 224 ok
il lato a è un intero e il lato b sarà 200·90/100 = 180
quindi a = 224 , b = 180, c = 100
Procedendo da 90/100 verso 99/100, i valori ottenuti per a non sono interi, tranne che in un caso:
per cos(ϑ) = 95/100 il valore di a è di nuovo un intero : 261.
Quindi ci sarebbe un altro triangolo ottusangolo con i lati interi di 100, 190, 261 e con un angolo acuto la metà dell’altro e minore di 30°.
Seguendo una via trigonometrica ho ottenuto due risultati possibili per il perimetro.
551 che corrisponde a b=190 a=261
504 che corrisponde a b=180 e a=224
Il procedimento è questo}=\frac{c}{sin(\theta)})
Per il teorema dei seni
poiché=2&space;sin(\theta)&space;cos(\theta))
ottengo che=\frac{b}{2c}=\frac{b}{200})
Questa relazione mette dei vincoli al valore di b.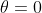
b<200 altrimenti il coseno non ha senso o
Per il teorema di Carnot
Poiché a è intero, b deve essere un multiplo di 10.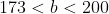
.
Questo vincolo si aggiunge ai 2 vincoli precedenti per i quali
Quindi b può essere 180 o 190.
per b=180 il perimetro è 504
per b=190 il perimetro è 551.
Ottimo Fabry a Andy! Il problema era estrarre dal cappello anche la seconda soluzione...
Sembra essere interessante anche generalizzare la faccenda e vedere il luogo dei punti del vertice più acuto del triangolo... Si può anche fare analiticamente... La geometria è come le "noccioline"... una tira l'altra!
Praticamente, considerando il triangolo 100, 180, 224, scomponendo i 3 valori in fattori primi, la scomposizione presenta un divisore comune che è 2 al quadrato ovvero 4, per cui il triangolo di lati la cui misura è 25, 45, 56, rappresenta il triangolo primitivo con le caratteristiche di avere:
1) un angolo ottuso;
2) i 3 lati di misura intera;
3) un angolo acuto la metà dell’altro;
4) l’angolo acuto minore inferiore a 30°
e che genera la famiglia di triangoli 25k, 45k, 56k, con k intero positivo, la quale possiede le quattro caratteristiche prima citate.
Mentre per il triangolo 100, 190, 261 non esiste un divisore comune, per cui è già il triangolo primitivo, che genera la famiglia di triangoli 100k, 190k, 261k con k intero positivo, con le stesse caratteristiche di cui sopra.
ottima considerazione Andy! Belle queste famiglie di triangoli ... Più in generale, dato un triangolo con i lati interi, esistono ovviamente infiniti triangoli simili ad esso con i lati interi. Basta trovare il "capofamiglia" che ha lati interi senza un divisore comune. Sono sicuramente capifamiglia i triangoli che hanno lati interi primi. E' proprio vero, basta un triangolo e se ne possono scrivere libri interi...
Il luogo dei punti del vertice A sembrerebbe essere una circonferenza con centro nel vertice B di raggio pari alla lunghezza del lato c
Le coordinate del punto A in un riferimento centrato nel vertice B e asse x lungo il lato a:
Sommo i quadrati delle due coordinate:
Per il teorema di Carnot=c^2)
Quindi ottengo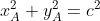
che è l'equazione di una circonferenza di raggio c centrata nell'origine che ho fissato nel vertice B.
Mi accorgo che non serviva lo sviluppo che ho fatto sopra. La distanza di B da A è c che rimane costante per la definizione del problema. Se B è fisso, A percorre una circonferenza come in un sistema biella-manovella.
Forse non era questo il luogo dei punti che chiedevi.
Forse non ci siamo capiti...
Se b = 200 cos(teta)
All'estremo in cui teta = 30 si ha b = 173, mentre all'estremo in cui teta = 0 abbiamo b = 200.
Sembrerebbe un'ellisse con centro in A
Spiego meglio come costruire il triangolo ABC per i valori ammessi di teta.
Ci sono tutti i dati per determinare il luogo dei punti C che può assumere il triangolo al variare di teta...
Chi avesse voglia...
Generalizzando la figura, il luogo dei punti di C visto da A, cioè con A fisso, mi sembra sia questo.
Appena posso controllo di nuovo e cerco di spiegare meglio.
Per confrontare meglio le figure. inverti A con B e fai girare in senso antiorario AC = b. Ricordiamoci che b = 200 cos (teta). Il che sembra tornare, ma tu hai fatto girare AC anche quando diventa acutangolo... Cambiano le condizioni di partenza...
Ho capito cosa hai fatto (credo). Hai proseguito anche se l'angolo ottuso diventava quello in B. Non capisco, però, la curva più stretta... Riempiendo la parte inferiore dovrebbe esserci un semplice ribaltamento.
Ho capito, hai considerato il triangolo piccolo invertendo ancora gli angoli...
Mi sono totalmente perso questa interessante dissertazione a causa di una epica lotta condominiale in vista di una tumultuosa assemblea e per contemporanee complicazioni per riuscire a rinnovare una carta di credito a cui sono associati pagamenti automatici per vari servizi vitali, mail e pec.
Problemi non ancora risolti.
Comunque, guardando la curva, mi sembra di riconoscere una epicicloide/cardioide.
Dalle equazioni si potrebbe capire se lo è davvero ma non mi ci posso dedicare con calma per i motivi citati.
Lascio a voi questa verifica, se vi sembra ne valga la pena.
Buon lavoro.
Cerco di spiegare come è nata la curva dell'animazione.
Per provare a rispondere alla domanda su luogo dei punti di C, ho cercato l'equazione di questa curva.
Le equazioni parametriche che ho trovato sono queste (nella versione utilizzata da Enzo nelle ultime figure):
&space;\cos(3\theta))
Si riferiscono alle coordinate di C rispetto ad un riferimento centrato in A con asse x lungo AB.
Giustamente Enzo ha fatto notare che AC non può andare oltre l'allineamento con AB che avviene per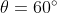
Infatti, per come è definito il problema di partenza,
può essere nell'intervallo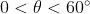 
.
Valori maggiori di 60° non sono possibili perché l'altro angolo sarebbe maggiore di 120° e
già la somma dei 2 angoli sarebbe maggiore di 180°.
Comunque l'equazione parametrica ammette valori per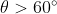
. Gli si può dare un significato geometrico cambiando la definizione degli angoli.
Provo a spiegarmi con una figura.
A sinistra il triangolo con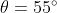
prima dei 60°. I triangoli rosso e blu sono lo stesso triangolo ruotato. Qui gli angoli 
e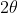 
sono interni al triangolo come nella definizione iniziale. Nella figura rossa B è a destra di C. Quindi, nella figura blu ruotata appare al di sopra dell'asse AB.
A destra il triangolo con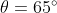
, quindi dopo i 60°. Gli angoli 
e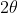 
sono misurati in continuità con la figura precedente, ma non sono più angoli interni. Nella figura rossa B ha scavalcato C. Quindi, nella figura blu ruotata appare al di sotto di AB. Il triangolo si è iniziato a rimpicciolire con C che si è avvicinato ad A.
Con questa definizione degli angoli rimangono valide le equazioni parametriche anche per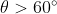
e la curva del luogo dei punti di C appare così:
Mi rimane il dubbio se questa curva ha un nome.
Quando sopra dico "Quindi, nella figura blu ruotata appare al di sotto/sopra di AB. " mi riferisco al punto C.
A e C continuano ad avvicinarsi fino a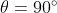
. Poi riprendono simmetriche fino a 
.
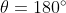Dopo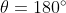
la figura si ripete.
Caro Fabry (e non solo).
Direi di fare il punto della situazione.
Una delle condizioni di partenza era che l'angolo in A fosse ottuso. Ciò va bene fino a 2 teta uguale a 60°. Poi viene abolita la prima condizione, ma rimane quella in cui l'angolo in C sia la metà di quello in B e abbiamo la curva di sinistra che tende a raggiungere il punto B. Già qui c'è una degenerazione della curva. Se proseguiamo al di sotto dell'asse x, annulliamo anche la seconda condizione, dato che è l'angolo in C a diventare il doppio di quello in B. Temo che ciò che si stia facendo sia un poco confusionario. Al massimo, mi limiterei alla parte che ho disegnato nella figura a colori di qualche commento fa. Ma anche così, ho paura che vi siano in realtà due funzioni che giocano... La parte per noi significativa è solo quella tra 2 teta uguale a zero e 60°.
Mi piacerebbe scrivere l'equazione in coordinate cartesiane (non polari) di questo tratto di curva. Basterebbe trovare l'intersezione tra la retta per A di coefficiente tan (2 teta) e quella per B di coefficiente tan(3 teta). Sia tan 2 che tan 3 possono scriversi in termini di m = tan (teta).
Fate voi... Fourier mi aspetta...
Il tempo, però, mi manca... e potremmo anche sospendere qui la trattazione...
dalla figura del commento precedente (2 maggio ore 8 57)
Assumendo l'origine nel punto B le equazioni delle due rette sono
y = tan (2 teta) *x
y= tan(3 teta) (x-100)
Uguaglio le due espressioni di y e ottengo
x = 100* tan(3 teta) / (tan(3 teta) - tan (2 teta)
Esprimendo 2 teta e 3 teta in funzione di teta :
tan (2 teta) = (3 tan(teta) - tan^3(teta) ) / (1 - 3 tan^2(teta) )
tan (3 teta) = 2 tan(teta) / 1-tan^2(teta)
Indico tan(teta) con il simbolo "t"
sostituendo e semplificando (salvo errori) arrivo a questa espressione di x:
x= 100 * ( t^5 - 4 t^3 + t) / (t^5 + 2 t^3 + t)
La funzione inversa che fornisce t(x) è la seguente:
t = +- radq( ( -x -10*radq(6) * radq(x +50) -200 ) / ( -x +10*radq(6) * radq(x +50) -200 ) )
Ora il valore t(x) andrebbe sostituito nella espressione di y
y = (3t -t^3 ) * ( x -100) / (1-3 t^2) per ottenere l'equazione cartesiana della curva descritta dal punto C
Non andrei oltre, (anche perché devo tornare ad occuparmi della mega assemblea di condominio)
Per Fabry,
ritornando a bomba... direi che tutto il succo del discorso è ben evidenziato dalle coordinate polari, quando C arriva vicino a B. per 3teta = 180, abbiamo proprio che x = - 100.
Basta provare per 3teta = 179...
x = - 2 cos(59.67)cos(179) = -1.001
In poche parole sembrerebbe arrivare all'assurdo che teta tenda a 60° mentre 2teta tenda a 120°.
Possiamo dire che la curva degenera? A questo punto si può andare oltre, ma 3teta deve assume un valore negativo (non certo maggiore di 180) e tutto dovrebbe ribaltarsi... In tal modo non si scambiano tra loro gli angoli teta e 2 teta.
Boh... non riesco a proseguire con altra logica
Proprio così Mau! Vorrei proprio sapere che curva viene fuori tra teta = 0 e 30
Lo vorrei propri sapere anche io ma l'equazione diventa molto complessa.
Appena posso provo a scriverla con latex, ma è un lavoro certosino.
La rappresentazione della formula cartesiana in Latex è talmente articolata da essere illeggibile.
Preferisco mostrare nella figura la curva costruita per punti tra 0° e 30° e il suo confronto con un arco di cardioide costruito con la stessa scala, da cui si vede che NON è una cardioide anche se ha una certa somiglianza.
Una banale correzione nel disegno: La linea verticale rossa corrisponde al calcolo per teta=30° , come vedete nella figura sottostante e non a teta = 90° (come scritto nella figura del commento precedente). L'angolo di 90° ( = 3 teta) è quello formato tra la linea verticale e l'asse x.
Riprendendo il discorso sulla famiglia di triangoli, la chiave principale di tutto il meccanismo, per determinare una terna con le condizioni del quiz, è il vincolo per il quale ϑ deve essere minore di 30°, che equivale a dire che cos(ϑ) > 0,866.-1))
(e b = 2c·cos(ϑ) ) posso scegliere un valore intero di c “ad hoc” per ricavare a, ad esempio c = 16:
^2&space;-&space;1))
= 32,1….
^2&space;-&space;1))
= 32,56….
^2&space;-&space;1))
= 33 ok → b = 2·16·(224/256) = 28 → triangolo 16, 28, 35 primitivo caratteristico;
^2&space;-&space;1))
= 175 → b = 144 triangolo 81, 144, 175 primitivo caratteristico.
^2&space;-1))
= 1267,25 no
^2&space;-1))
= 1311 → b = 1100 triangolo 625, 1100, 1311 primitivo caratteristico
^2&space;-1))
= 1355,25 no
^2&space;-1))
= 1400 → b = 1125 triangolo 625, 1125, 1400 derivato da 25k, 45k, 56k per k = 25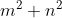
,
,
;
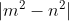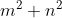= 6/4 + 2/4 = 8/4 = 2 ipotenusa
= 2·√12 / 4 = √3 cateto maggiore
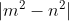= |6/4 – 2/4| = 4/4 = 1 cateto minore
Che poi il decimale venga espresso sotto forma di frazione con il denominatore potenza di 10 o potenza di qualunque altro numero, la cosa è equivalente perché con le semplificazioni tra numeratore e denominatore si ottiene un decimale esprimibile in decimi, centesimi, millesimi, etc. etc.
E siccome 10 si scompone in 2×5, una potenza di 10 equivale a 2 elevato alla stessa potenza per 5 elevato alla stessa potenza. Queste ovvietà si possono visualizzare con un esempio concreto:
se volessi esprimere la frazione come rapporto con una potenza di 2, per esempio 256, la condizione si scriverebbe cos(ϑ) ≥ 222/256 ≈ 0,867 e dato che
oppure se esprimessi la frazione con il denominatore potenza di 3, ad esempio 9, e c = 81 (che è 3 alla 4), avrei una solo opzione: cos(ϑ) ≥ 8/9 = 0,8 periodico, per cui
Nell’esempio del quiz, il dato fornito è c = 100, cioè potenza di 2×5, quindi se volessi immettere una misura “ad hoc” per c, potrei scegliere ad esempio 625 (5 alla 4) e allora avrei:
continuando per numeratori pari (92, 94, 96, 98) si ottengono altri quattro triangoli caratteristici e primitivi:
c b a
625, 1150, 1491
625, 1175, 1584
625, 1200, 1679
625, 1225, 1776
Il ragionamento sembra avere una qualche similitudine con la determinazione delle terne pitagoriche partendo da due numeri interi m ed n coprimi fra loro, uno pari l’altro dispari, generatori dei tre lati di un triangolo rettangolo:
lato1 =
lato2 =
lato3 =
nel caso del quiz, con il valore limite di ϑ = 30° , m ed n non sono più due interi ma due irrazionali positivi:
m = √6 / 2 ed n = √2 / 2 :
angoli acuti 30° e 60°, l’angolo ottuso "degenera" nell’angolo retto.
Riguardo il significato della curva per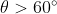
, penso che si possa trovare una logica per l'equazioni che governano la posizione di C rispetto ad A anche quando 
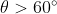se si considerano gli angoli riferendoli al sistema di riferimento. D'altra parte le equazioni stesse sono riferite al sistema di riferimento.
Se posiziono il triangolo in un riferimento che ha l'asse x allineato con CB, posso definire
come l'angolo tra CA e l'asse x nel verso positivo e l'angolo in B, quello che deve essere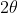 
, come l'angolo tra BA e l'asse x negativo. Inizialmente i due angoli sono interni al triangolo come nella definizione del problema iniziale.
Per
Per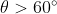
è ancora possibile realizzare un triangolo con l'angolo in B di valore 
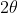se definito come sopra.
L'angolo
appare nella equazione parametrica delle coordinate di C rispetto ad un riferimento centrato in A con asse x allineato ad AB. In questo riferimento è l'angolo tra AC e l'asse x positivo che vale 
. Questo angolo continua a valere 
anche per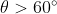 
con valori di 
che vanno oltre i 180°. Sotto ci sono i triangoli ruotati con AB allineato con l'asse x orizzontale.
Mamma mia, mamma mia... questo triangolo ha scatenato le migliori menti del circolo!!
Sono d'accordo con Fabry, quando persiste a far girare teta e a fare aumentare ancora l'angolo oltre i 60°. Ossia capisco la sua strategia. Tuttavia, penso che anche in questo modo si continui a imporre una certa condizione, ossia un angolo metà dell'altro. Questa condizione porta a una certa curva. Non è, però, del tutto insensato, far comandare tutto da 3 teta e dire che raggiunto 180° torna indietro passando a valori negativi. Il triangolo continuerebbe ad avere un angolo doppio dell'altro. Insomma, direi che ci si presenta un bivio a teta = 60 o, meglio, a 3 teta uguale a 180.
Mau ha trovato ciò che pensavo: non è una cardioide...
Andy vola nella matematica e non disdegna di accostarsi alle terne pitagoriche.
Fatemi dire che la geometria, insieme a sua sorella matematica, riescono a dare dignità e complessità anche a un semplice triangolo ottusangolo. Merito, soprattutto, di chi affronta i problemi senza timore e con rispetto.
Io suggerei di concludere qui questo quiz (ne ho un altro nel cassetto, parimenti pronto a estendersi a valanga). Tuttavia, se qualcuno di voi vuole andare oltre e descrivere la sua trattazione con relativa semplicità e completezza, è libero di farlo e il suo lavoro verrà ovviamente pubblicato e apprezzato.
Aggiungo solo una punto che avevo quasi pronto.
L'equazione implicita che corrisponde alle equazioni parametriche che ho scritto sopra potrebbe essere questa: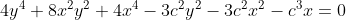
Il 4° grado giustifica la molteplicità di valori su alcune verticali e alcune orizzontali.
Poi, per passare la parola alle serie di Fourier le equazioni parametriche possono essere scritte come piccole serie:
Solo per completare il confronto sulla curva completa.
La linea rossa corrisponde alla cardioide, quella blu alla curva in questione.
Sembrerebbe una curva simile alla chiocciola di Pascal...
una semplice descrizione delle caratteristiche e della equazione polare ed implicita della lumaca di Pascal si trova a questo indirizzo.
In effetti è una quartica come quella che stiamo osservando, ma la costruzione, molto semplice, descritta nella pagina referenziata è diversa da quella che abbiamo realizzato.
Credo che l'intuizione di Andy fosse corretta e la curva animata di Fabrizio possa avere un nome preciso.
Ho sovrapposto la curva della animazione con la curva della lumaca di Pascal e il risultato è sorprendente. Coincidono perfettamente.
La verifica analitica si potrebbe fare dimostrando che, una volta tracciato il cerchio di raggio AB con centro nel punto A, e il segmento BC ( il lato del triangolo) il punto del cerchio intersecato da BC è medio tra le intersezioni di BC con il lobo interno e quello esterno della curva. Ossia le due distanze indicate con "k" sono uguali e restano costanti durante la rotazione di BC.
La figura che vedete sopra è la sovrapposizione di queste due:
Ma forse la dimostrazione non serve se confrontiamo le equazioni della chiocciola :
con quelle (strutturalmente molto simili ) indicate da Fabrizio nel suo ultimo commento
"Poi, per passare la parola alle serie di Fourier le equazioni parametriche possono essere scritte come piccole serie:
Dalle equazioni parametriche messe a confronto da Maurizio sembra che il luogo dei punti della curva che abbiamo ottenuto sia un caso particolare della lumaca di Pascal proposta da Andy, solo traslata di c lungo l'asse x. Traslazione ragionevole poiché ho ottenute le equazioni parametriche centrando la curva su A, invece la Lumaca è centrata sul punto che abbiamo chiamato B.
Il caso particolare sarebbe questo c=b=2a, (qui b ed a sono quelli della curva parametrica della Lumaca non i lati del triangolo).
Per completare il confronto dobbiamo ridenominare i due parametri angolari. per non confonderli tra loro. Lasciamo il nome
a quello della curva derivata dal triangolo e chiamando 
quello della lumaca.
Ponendo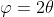
si ha la stessa curva. Non ci perdiamo nulla perché comunque 
completa la curva a 180°.
Le vostre lumache sono bellissime... tuttavia, resto dell'idea che non si possano trasformare troppo le ipotesi di partenza. Ammettiamo pure che l'angolo in A sia acuto, ma dobbiamo far restare immutata la regola che l'angolo in C sia 1/3 di phi e l'angolo in B i 2/3 phi. Secondo me non più senso la curva completa...
Facciamo ruotare soltanto il lato AC secondo l'angolo phi... Cosa succede realmente con queste ipotesi in gioco?
Succede questo...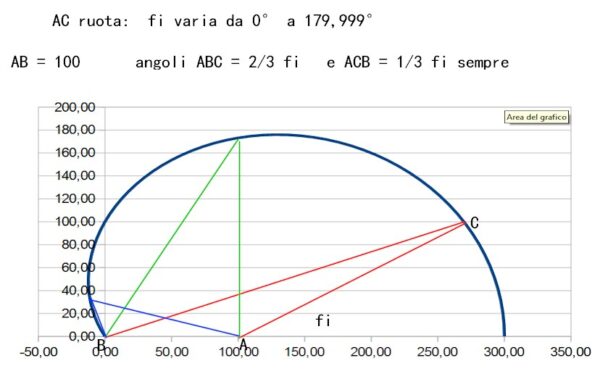
La curva è un arco di chiocciola di Pascal, tra fi = 0° e fi = 179,999°.
Se prendiamo tutti i valori di
indicati da Enzo, 
, possiamo (quasi) chiudere la curva. Abbiamo la parte esterna della curva precedente. L'equazione parametrica è la stessa, ma è limitato il suo campo di esistenza.
Infatti, la chiocciola secondo me dovrebbe essere interrotta e poi ribaltarsi attorno all'asse x...
Chiederei a Fabrizio di mostrarmi con chiarezza il triangolo ABC dopo che è stata toccata la parte negativa delle x (fi = 18o°). A me non torna con il nostro triangolo di partenza, pur accettando angoli acuti in A.
Se, poi, volessimo cambiare teta con 2teta avremmo una curva differente da tutte le altre...
Secondo me è sbagliato trattare la lumaca anche dopo che 3teta= 180. Vorrei, infatti, vedere cosa diventa il nostro triangolo di partenza, che DEVE rimanere sempre un triangolo con un lato fisso uguale ad AB e, al limite, avere sempre un angolo che è doppio dell'altro (ammettendo pure di invertirli...).
Caro Mau,
lo so benissimo, come già mostrato in un commento "a colori" di qualche giorno fa. Il problema nasce quando si vuole continuare a far variare teta... non ha più nessun legame con il trinagolo, a meno che non sia rimbambito del tutto.
Nel mio ultimo commento, infatti, ho limitato l'angolo phi per non superare i 180° e ho ignorato i valori negativi perché l'arco che si ottiene ribaltando la figura attorno all'asse x, riguarda triangoli speculari che, essendo congruenti con quelli dell'arco superiore, non aggiungono nulla di nuovo.
Per come la vedo io il campo di validità va da 0° a 180° (escluso).
Chiarisco meglio: l'angolo phi deve variare da 0° a 60° (esclusi) affinchè l'angolo 3 phi non superi i 180°
Avendo visto che il requisito su
era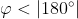 
, l'ho interpretato come 
.
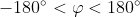Se invece va interpretato come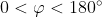
rimane solo la parte superiore della curva.
Nel caso fossero accettabili anche angoli negativi, dobbiamo considerare l'orientamento degli angoli.
Come dice Maurizio, i triangoli sotto sono speculari a quelli sopra. Quindi, i triangoli sotto hanno gli angoli che vanno in senso opposto a quelli corrispondenti del triangolo sopra. Questo significa che se le relazioni tra gli angoli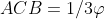
e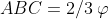 
sono valide per il triangolo sopra, rimangono valide anche per quello sotto.
Riassumiamo i concetti base...
Se l'angolo più piccolo è quello che si muove, otteniamo la figura descritta a colori fin dall'inizio che poi è costretta a ribaltarsi. Se invertiamo i due angoli si ottiene una figura molto diversa che deve anch'essa ribaltarsi. Tra le due figure non vi è possibilità di unione (mezza una e mezza l'altra), dato che la funzione completa non si chiude.
Bene, passiamo ad ... Arogatip
Aggiungo ancora...
con un po' di attenzione potremmo legare il nostro triangolo alla costruzione della lumaca fatta dal grande Durer e lasciata senza nome. Intravvedo angoli doppi e altri parametri che potrebbero spiegare la lumaca con la cuspide e senza anello interno. Insomma, la nostra curva, semplicemente ribaltata dopo 180° (forse scambiando gli angoli)
https://www.webfract.it/RODONEE/Lumaca2.htm
E anche questa costruzione...
https://www.macchinematematiche.org/index.php?option=com_content&view=article&id=131&Itemid=212&lang=it
Mi sa che potrebbe essere una cardiode, facendo ruotare il lato noto... Basta... sono troppo stanco!
Dalla sovrapposizione mi risulta una certa somiglianza ma non totale.
Una sovrapposizione più accurata mostra comunque ottima approssimazione parziale e uno scostamento deciso oltre un certo punto.