Per capire meglio il tutto, facciamo ora un classico esempio, considerando una funzione f(t), periodica, moto particolare che richiama un segnale  “a scatti”.

Prendiamo i nostri assi cartesiani e disegniamo due rette parallele all’asse delle ascisse, in particolare

y = 1

y = - 1

Inseriamo un funzione periodica che valga 1 tra l’origine e metà del periodo P, mentre valga – 1 tra la metà del periodo e il periodo completo. La mostra chiaramente la Fig. 5.

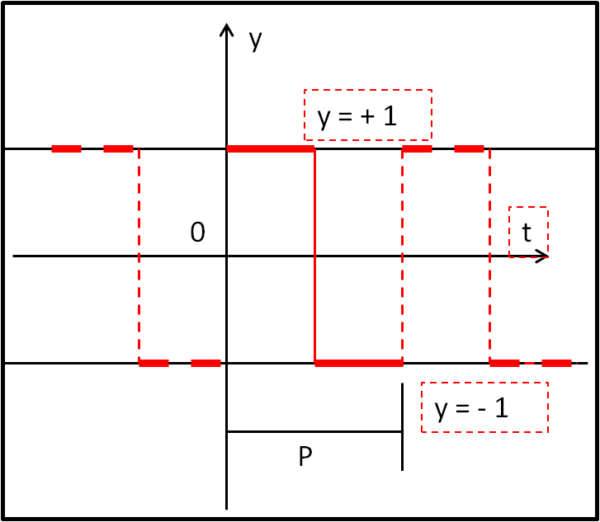
Abbiamo anche disegnato (a tratteggio) la funzione per valori negativi del tempo t e per valori successivi al periodo P.

Cerchiamo, allora, di svilupparla in serie di Fourier.

Riscriviamo, ancora una volta,  la serie di Fourier in modo generale con il valore dei suoi coefficienti:

f(t) = a₀ + ∑₁^∞ a_m cos(m(2π/P)t) + ∑₁^∞ b_m sin (m(2π/P)t)

a₀ = (1/P) ∫_-P/2^P/2 f(t) dt

a_m = (2/P)∫_-P/2^P/2 f(t) cos(m(2π/P)t) dt

b_m = 2/P ∫_-P/2^P/2 f(t) sin(m(2π/P)t) dt

Iniziamo con il calcolo di a₀.

Notiamo che, spesso, per questa trattazione, si prende, come periodo, proprio 2π, in modo da semplificare i calcoli. Tuttavia, noi mostriamo che questa scelta “ad hoc” non è essenziale, anche se alla fine ne approfitteremo.

Il valore di a₀ non avrebbe nemmeno bisogno di un calcolo completo, dato che il suo valore è abbastanza immediato. Esso, infatti, non è altri che l’integrale della funzione tra – P/2 e 0 e tra 0 e P/2, come si vede in Fig. 6.

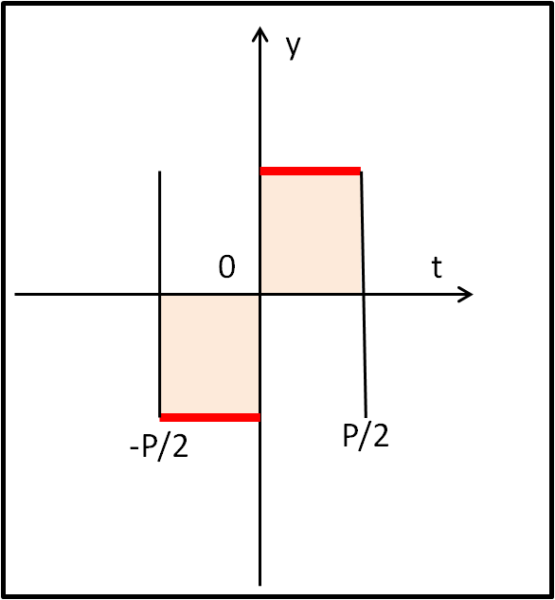
E' immediato concludere che le due aree descritte dagli integrali (in rosa) sono uguali e di segno contrario. Il che vuol dire che la loro somma risulta essere ZERO.

Tuttavia, facciamo le cose per bene e calcoliamoci l’integrale che descrive a₀:

a₀ = (1/P) ∫_-P/2^P/2 f(t) dt = (1/P) ∫_-P/2⁰ f(t) dt + (1/P) ∫₀^P/2 f(t) dt

Ma tra – P/2 e 0 la funzione vale -1, mentre tra 0 e P vale + 1, perciò:

a₀ = (1/P) ∫_-P/2⁰ (-1)dt + (1/P) ∫₀^P/2 (1)dt = - (1/P) ∫_-P/2⁰ dt + (1/P) ∫₀^P/2 dt

a₀ = -1/P [t]_-P/2⁰ + 1/P[t]₀^P/2 = -1/P(0 - (- P/2)) + 1/P(P/2 – 0) = -(1/P)(P/2)+ (1/P)(P/2)

a₀ = - ½ + ½ = 0

Il valor medio della funzione è zero, come si poteva immediatamente capire guardando il grafico, ma trafficare con gli integrali, anche se banali, non può che aiutare a prendere dimestichezza con questa operazione non certo tra le più semplici.

Passiamo, ora, ai coefficienti a_m

a_m = (2/P)∫_-P/2^P/2 f(t) cos(m(2π/P)t) dt

A questo punto ci serve moltissimo quanto scritto sulla parità delle funzioni. Guardiamo bene la Fig. 6 La funzione è sicuramente DISPARI (simmetria rispetto all’origine). Gli integrali che permettono di calcolare a_m sono tutti relativi a dei coseni, che sono funzioni pari. Essi, perciò, non possono certo contribuire allo sviluppo in serie di una funzione dispari e devono essere tutti nulli. Comunque sia, proviamolo rigorosamente .

Forza e coraggio...

a_m = (2/P)∫_-P/2^P/2 f(t) cos((m2π/P)t) dt = (2/P)(∫_-P/2⁰ - cos((m2π/P)t) dt + ∫₀^P/2cos((m2π/P)t) dt)

Ricordiamo che

∫_a^b cos(kt) dt = 1/k∫_a^b k cos(kt)dt = 1/k[sin(kt)]_a^b

Per cui, ricordando anche che sin(-a) = sin(a)

a_m = (2/P)((P/2mπ)[sin((m2π/P)t)]_-P/2⁰ + (P/2mπ)[sin((m2π/P)t)]₀^P/2)

a_m = (2/P)((P/2mπ)(0 - sin(mπ)) + (P/2mπ)(sin (mπ) - 0))

a_m = (2/P)(- (P/2mπ)sin(mπ) + (P/2mπ)sin(mπ)) = 0

No, non abbiate paura... qualcosa alla fine rimarrà!

Andiamo a prenderei coefficienti b_m, quelli che accompagnano la funzione seno. Il seno è funzione dispari e quindi sembrano proprio quelli giusti per cercare di approssimare la nostra f(t) che è chiaramente dispari.

b_m = 2/P ∫_-P/2^P/2 f(t) sin(m(2π/P)t) dt

b_m = 2/P (∫_-P/2⁰f(t) sin(m(2π/P)t) dt + ∫₀^P/2f(t) sin(m(2π/P)t) dt)

b_m = 2/P (∫_-P/2⁰(-1) sin(m(2π/P)t) dt + ∫₀^P/2(1)sin(m(2π/P)t) dt)

b_m = 2/P (- ∫_-P/2⁰ sin(m(2π/P)t) dt + ∫₀^P/2 sin(m(2π/P)t) dt)

Per semplificare il calcolo, fatemi scrivere:

k = m2π/P e ricordare che cos(- a) = - cos(a)

b_m = 2/P (- ∫_-P/2⁰ sin(kt) dt + ∫₀^P/2 sin(kt) dt)

b_m = 2/P (- (1/k)∫_-P/2⁰ k sin(kt) dt + (1/k)∫₀^P/2 k sin(kt) dt)

b_m = 2/P (+ (1/k)[cos (kt)]_-P/2⁰ - (1/k)[cos (kt)]₀^P/2 )

b_m = 2/P (+ (1/k)[1 – cos (kP/2)] - (1/k)[cos (kP/2) - 1])

b_m = 2/P ( (1/k)[1 – cos (kP/2]  + (1/k)[1 - cos (kP/2)])

b_m = 4/P (1/k)[1 – cos (kP/2)]

Rimettiamo a posto il k

b_m = 4/P (P/m2π)[1 – cos ((m2π/P)(P/2))]

b_m = 2/(mπ)(1 – cos(mπ))

E’ stata dura, ma ce l’abbiamo fatta!

Ma ne siamo sicuri? Riflettiamo un attimo su

cos(mπ)

Se m è un numero pari (2, 4, 6, ...) il coseno è sempre uguale a uno.

Ma se il coseno è uguale a 1 il termine dentro parentesi si annulla e quindi tutti i termini con m pari diventano ZERO.

Se m è invece un numero dispari tutti i coseni sono uguali a -1 e quindi abbiamo finalmente qualcosa che non si annulla. Ne segue che:

b_m = 0                 con m pari

b_m = 4/(mπ)       con m dispari

Lo sviluppo in serie di Fourier diventa allora:

f(t) = ∑₁^∞ b_m sin (m(2π/P)t)

Per sfruttare quanto trovato poco sopra, dividiamo la somma in due somme: quella con i termini pari e quella con i termini dispari

f(t) = ∑₁^∞ b_2m sin (2m(2π/P)t) + ∑₀^∞ b_2m+1 sin ((2m + 1)(2π/P)t)

Non è cambiato niente, dato che la prima somma mi fornisce i termini pari, b₂, b₄, b₆,…, mentre la seconda i termini dispari, b₁, b₃, b₅, …

Eh sì, possiamo semplificare ancora di più la nostra serie, dato he la prima sommatoria ha solo i termini pari che, come abbiamo appena dimostrato, valgono tutti ZERO. La serie diventa:

f(t) = ∑₀^∞ b_2m+1 sin ((2m + 1)(2π/P)t)

non solo, però… abbiamo anche visto che i coefficienti dispari hanno la forma

b_m = 4/(mπ)       con m dispari

Si ottiene, allora:

b_m+1 = 4/(2m + 1)π)

per cui:

f(t) = ∑₀^∞ 4/((2m+1)π)) (sin ((2m + 1)(2π/P)t)

Finalmente l’abbiamo ridotta ai “minimi termini” e possiamo controllare se una funzione continua (la serie) riesce ad approssimare una funzione discontinua (f(t)).

Non ci resta che calcolare uno a uno tutti i termini della sommatoria e vedere che contributo danno. Ovviamente, non possiamo andare veramente fino a infinito, per cui sommeremo solo i primi termini, più che sufficienti per vedere cosa succede.

Cominciamo con m = 0

f(t) = (4/π) sin(2πt/P)

Per comodità di calcolo prendiamo pure il nostro periodo uguale a 2π, ma potevamo prendere un qualsiasi valore.

f(t) = (4/π) sin t

Confrontiamo in Fig. 7, questo primo termine (in verde) con la funzione a scatti (in giallo) di Fig. 5.

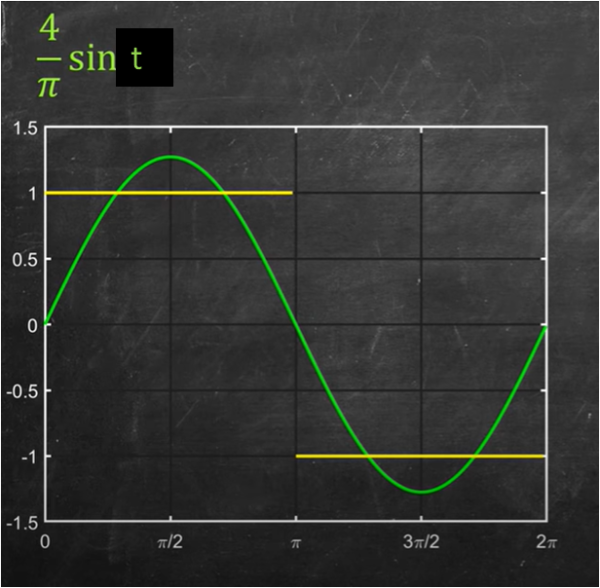
Beh... un po' le assomiglia, ma non certo in modo soddisfacente. Non abbattiamoci e passiamo al secondo termine:

m = 1

f(t) = 4/(3π) sin (3t)

Sommiamo questo termine a quello precedente

f(t) = (4/π) sin t + 4/(3π) sin (3t)

e costruiamo la Fig. 8, dove si confronta il risultato con la funzione di partenza.

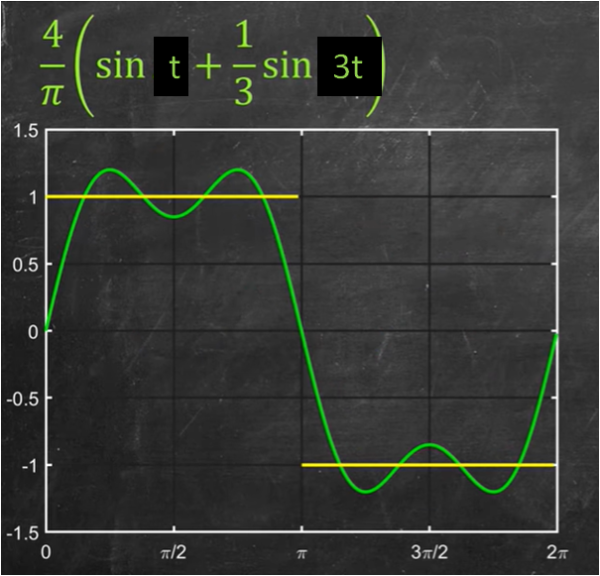
Il gioco ormai è piuttosto chiaro, ma vale la pena mostrare il risultato (Fig. 9) quando si aggiunge anche il termine successivo (m = 2), ossia quando la serie vale

f(t) = (4/π) sin t + 4/(3π) sin (3t) + 4/(5π) sin (5t)

Per concludere disegniamo, in Fig. 10, il risultato per una serie formata da 19 termini.

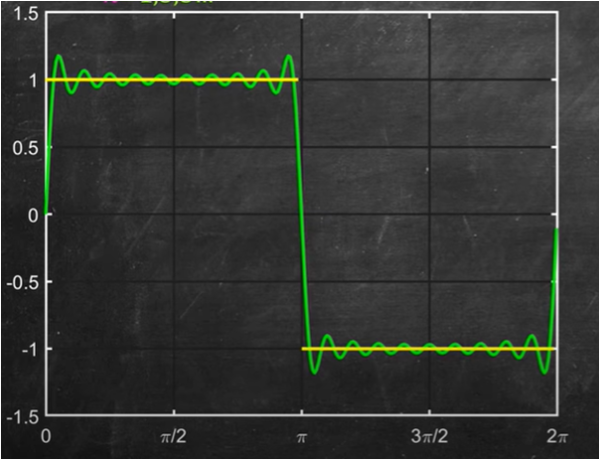
La situazione è nettamente migliorata, ma, avendo a disposizione un semplice computer, non è difficile pensare come i termini a disposizione possano diventare centinaia, migliaia o quello che volete. La nostra funzione discontinua "a scatto" viene così trasformata in una funzione continua formata solo da seni.

Dopo aver introdotto una nuova e importantissima funzione che sarebbe meglio chiamare distribuzione (delta di Dirac), aver giocato ancora un po' con la serie di Fourier (utilizzando il piano complesso), faremo un nuovo esempio ... non mollate!

continua...

 

La serie di articoli dedicati alla serie di Fourier è disponibile QUI

e fanno parte del corso completo di matematica