(QI) Verso la soluzione del teorema di Arogatip **
Continuiamo la nostra leggenda pitagorica...
Pitagora aveva praticamente tappezzato la casa di famiglia di triangoli rettangoli, con tanto di quadrati costruiti sui suoi lati. E non perdeva occasione per vantarsi della magnifica scoperta. La rabbia di Arogatip cresceva giorno dopo giorno e quella figura geometrica era diventata la sua ossessione. Un giorno decise di passare all'azione proprio sfruttando il triangolo del fratello, con quelle invadenti appendici quadrate.
L'idea, molto semplice a parole, era quella di generalizzare il teorema del fratello. In poche parole costruire dei quadrati su un triangolo qualsiasi. Sarebbe stato un bello schiaffo alla arroganza di Pitagora. Purtroppo, però, Arogatip non conosceva la trigonometria e Carnot non era ancora nato (anche se altri prima di lui avevano risolto il problema).
Niente da fare, quei quadrati erano ben lontani dal mostrare un legame veramente stretto con i lati del suo triangolo qualsiasi... però, però... qualcosa poteva venire fuori, magari limitandosi ai triangoli. Ed aveva ragione, accidenti!
Un bel teorema, sicuramente, ma niente a che vedere con quello del più celebre fratello. Tuttavia, secoli e secoli dopo i matematici tornarono alla sua configurazione geometrica e vi scoprirono tutto e di più...
Non vi resta che completare l'approccio e il risultato di Arogatip...






9 commenti
Cari amici, colgo l'occasione del momentaneo silenzio del graforroico Mau, per proporre alcune divagazioni su caratteristiche quasi-pitagoriche del triangolo scaleno.
Questo triangolo è meno aristocratico e molto più democratico del triangolo rettangolo, tanto caro a Pitagora. Eccolo in una sua tipica versione.
Mentre nel triangolo rettangolo c'è un lato dominante, solo perché più grosso degli altri, e per tale motivo ha un quadrato che da solo è la metà della somma di tutti i tre quadrati, nel triangolo scaleno vige una assoluta parità.
I tre trapezi gialli costruiti sui lati hanno la medesima area, indipendentemente dalla dimensione di ciascun lato. Un principio democratico tanto caro ad Arogatip, quanto inviso al fratello.
Partendo dal triangolo rosso, prolunghiamo il lato di lunghezza "a" nei due sensi e con il compasso della mutua riportiamo a sinistra e a destra la sua lunghezza "a".
Facciamo la stessa cosa con gli altri due lati di lunghezza "b" e "c".
Chiudiamo collegando i prolungamenti con i segmenti di lunghezza "2a", "2b", "2c" come si vede nella figura.
Appaiono così tre triangoli uguali con i lati "2a" "2b" "2c" che si sovrappongono nel triangolo centrale rosso. Ciascuno dei tre trapezi gialli ha quindi area = 3 volte quella del triangolo rosso.
Se poi andiamo ad unire aiutandoci con la riga ( il compasso è meglio riporlo perché già è molle e a lasciarlo in giro potrebbe rompersi del tutto) i vertici adiacenti dei tre trapezi, vediamo che appaiono tre triangoli identici a quello rosso, proprio attaccati per un vertice ad esso. Un'altra prova della "democrazia strutturale" amata da Arogatip.
Ora, se proprio volete variare la forma di questi tre triangoli identici, perché secondo voi la diversità nell'uguaglianza (delle loro aree) è una pregevole ricchezza, basta fare scorrere un loro vertice lungo la linea parallela ad un lato e avrete la forme che preferite per i vostri triangoli.
Ma, come dicevo, queste sono solo fantasie in attesa della soluzione.
caro Oreste,
penso che la tua soluzione sarebbe piaciuta molto al caro Arogatip. Forse, però, l'avrebbe trovata troppo elaborata (non diciamolo forte, ma non era poi un genio...).Il suo metodo era molto più diretto e ancor più pitagorico...
Caro Prof. Sono proprio contento che le sia piaciuta la storia del triangolo democratico, anche se non è la soluzione che chiedeva.
Adesso mi permetterei di domandarle un consiglio su cosa fare per il compasso molle, che è un grosso problema.
Io lo tengo nel freezer perché, con l'estate che incombe, non vorrei che si sciogliesse. Però la Ines dice che le altera il gusto dei gelati e surgelati.
Dato che con i quiz che girano ( penso a quello dei cerchi olimpici) ci sarà bisogno di farne così di cerchi, non vorrei che alla fine mi venissero fuori delle spirali invece che le circonferenze.
Ci vorrebbe un compasso che non si smolla mai.
In una cartoleria qui a Cuneo ne ho visto uno che non le posso dire la marca sa, per la praivasi, che costa pochi euri ma mi pare resistente.
Cosa faccio? Io lo comprerei.
Lei, a mio giudizio, cosa ne pensa?
Grazie Cerea.
caro Oreste,
forse la soluzione migliore sarebbe quella di munire il compasso di una molla che lo costringa a chiudersi una volta utilizzato. Bisogna stare attenti ai diti, ma uno come lei, che tratta con le castagne, dovrebbe saperne molto... Sarebbe così gentile di dire al suo mentore Maurizio di darci la soluzione finale? A me, purtroppo, oggi fanno una spiacevole iniezione in un occhio (spero non con il compasso) e per due giorni sarò inattivo...
ricerea
Caro Prof. prima di tutto le dico in bocca al lupo dei boschi per l'iniezione e le raccomando di non sforzarsi a leggere per quei due giorni, che tanto la terra gira lo stesso, come abbiamo capito da tempo
Appena vedo il mio mentitore trasmetterò la sua pregevole richiesta che faccio mia.
Però so già che lui considera la "soluzione finale" una delle pagine più oscure della storia dell'umanità, quindi la vedo dura.
P.S. il compasso "a molla" mi sembra già meglio del compasso molle. Grazie.
E va bene, via..
Le cose sono andate così: Arogatip aveva passato molto tempo a osservare il disegno che il famigerato fratello aveva scarabocchiato sul muro del portico sud nella casa paterna.
Fingendo di prendere il sole, Arogatip scrutava quelle linee perverse alla ricerca di qualcosa da dire di più e di meglio.
Una sera gli apparve Minerva, a cui aveva sacrificato cento tori, proprio per avere un consiglio. La dea gli disse semplicemente: "Arò, ma non vedi che ci sono tre triangoli uguali uguali se solo tiri tre linee in più?"
E tracciò con le divine dita le tre linee di collegamento tra i quadrati, completando la figura più o meno così:
Arogatip rimase allibito e fece appena in tempo a chiedere "Ok, divina, ma ... la dimostrazione?" che Minerva era già sparita.
Allora il giovane ricopiò il disegno su un foglio di cartoncino bristol 70 x 100, che aveva in casa, poi ritagliò pazientemente con un cutter il triangolo giallo e gli altri tre viola e li pesò a coppie in tutti i modi possibili con una bilancia molto precisa che si era fatto prestare dalla dea Themis, a cui aveva sacrificato cento tori.
Il risultato delle pesate mostrò che esisteva sempre un perfetto equilibrio.
Arogatip non fu mai in grado di fornire una dimostrazione più seria di questa. Il padre gli proibì di sacrificare altri tori a chicchessia.
La metodologia seguita da Arogatip nella ricerca della sua dimostrazione si basava sullo studio esaustivo di tutte le configurazioni possibili del triangolo di partenza.
Cominciò il primo giorno con un triangolo isoscele, fissando il valore dell'angolo più piccolo pari a un grado.
Il giorno successivo aumentò di un grado l'angolo, portandolo a due gradi.
Di giorno in giorno, dopo due mesi, arrivò a studiare il triangolo equilatero. e constatò che in quel caso particolare i conti tornavano in modo evidente.
Così si ritenne soddisfatto, anche convinto dal padre che non vedeva di buon occhio tutti quegli scarabocchi con cui il figlio aveva imbrattato per giorni e giorni le pareti domestiche.
Se qualcuno, volesse comunque provare a trovare una corrispondenza più generale tra le aree dei triangoli, suggerisco di osservare come vengono scomposti dalle rispettive mediane, come in questa figura: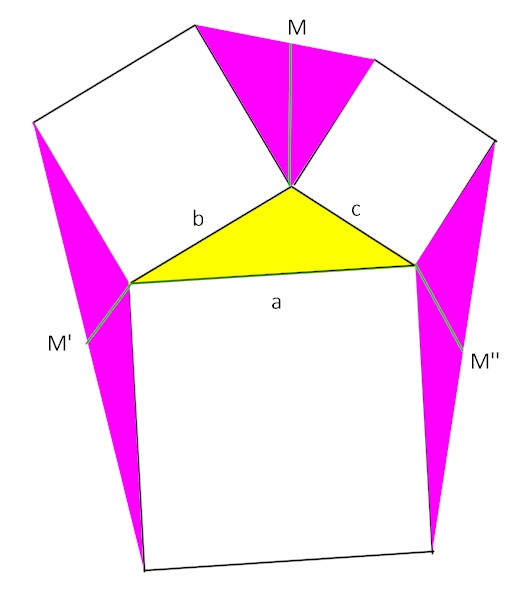
Visto che non ci sono state reazioni al suggerimento e non volendo deludere Enzo che ha sollecitato una soluzione finale, azzardo questa:
Presunta ipotesi di Arogatip:
dato un triangolo qualsiasi e costruiti i quadrati sui suoi lati, ciascuno dei tre triangoli interposti tra i quadrati è equivalente al triangolo dato, ossia ha la medesima area.
Pare che questa equivalenza esista realmente, come si vede nella figura sottostante.
I due angoli indicati con “alfa” sono uguali perché DC è perpendicolare a AC e MH è perpendicolare a AH
I due angoli indicati con “beta” sono uguali perché DC è perpendicolare a AC e NK è perpendicolare a DK
Per il secondo criterio di congruenza ( 2 angoli e il lato compreso uguali) DMC e CNA sono congruenti e i due triangoli rosa sono sovrapponibili.
Il medesimo ragionamento vale per i due triangoli azzurri EMC e CNB
Vale poi l'uguaglianza CM = AN = NB che equivale a dire che N è il punto medio di AB
e anche l'uguaglianza CN = DM = ME che equivale a dire che M è il punto medio di DE
Il ragionamento è il medesimo per uno qualsiasi dei tre triangoli interposti tra i quadrati.