Il linguaggio di Matlandia **
Come tutti sanno sullo strano e simpatico pianeta di Papalla esiste la Nazione di Matlandia, dove gli abitanti hanno ormai deciso di usare solo e soltanto il linguaggio della matematica per parlare tra di loro.
Due fratelli hanno ereditato un grande pezzo di terra, splendido per essere coltivato a papalpatate e a papalcarote. Decidono di cambiare lavoro e dedicarsi a questa coltivazione. Prima, però, devono andare a vedere il terreno che è teoricamente segnalato, ma è da tempo completamente invaso dalle erbacce e seguirne i confini non è cosa facile. Inoltre, decidono anche di costruire al suo interno una grande fattoria, dove trasferirsi con le rispettive famiglie (i bambini adorano le papalpatate e le papalcarote...).
E' necessario che vadano sul posto sia per misurare bene il terreno sia per scegliere il luogo dove costruire la nuova casa. Non vogliono, però, influenzarsi a vicenda nella misura e nella scelta. Concordano, perciò, di recarsi separatamente e di rivedersi dopo una settimana.
I due fratelli vanno nel luogo ereditato e poi si incontrano nuovamente. Il primo fratello dice: "ab/(a + b + c)". Il secondo fa un largo sorriso e risponde: "(a + b - c)/2". Si abbracciano contenti dato che la forma è la stessa, così come è la stessa anche l'idea sul luogo in cui costruire la casa!
Si chiede:
(1) Qual è la forma del terreno
(b) Dove intendono costruire la casa?






3 commenti
Bene... vedo che come al solito nessuno se la sente di provare. Diamo, quindi, via libera ai più esperti
Se le due affermazioni sotto forma di formule si equivalgono, allora deve essere che:
facendo i prodotti incrociati: 2ab = (a+b+c)(a+b-c)
Il prodotto al secondo membro è un prodotto notevole: [(a+b) + c]·[(a+b) - c] =^2&space;-&space;c^2)
per cui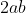 =
= 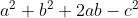 ; i doppi prodotti di ab al primo e secondo membro si elidono a vicenda e rimane
; i doppi prodotti di ab al primo e secondo membro si elidono a vicenda e rimane 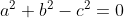 ovvero il teorema di Pitagora, quindi il terreno ha la forma di un triangolo rettangolo.
ovvero il teorema di Pitagora, quindi il terreno ha la forma di un triangolo rettangolo.
Per la scelta del punto sul quale erigere la casa, mi vengono in mente più opzioni:
1) l'incentro per avere 3 distanze costanti dai lati del triangolo;
2) il punto di Fermat per avere la minima somma delle distanze dai vertici;
3) il circocentro per avere una distanza costante dai vertici;
4) il baricentro per avere una distanza "mediata" dai lati;
5) nessuno di questi....
ottimo inizio, ancor uno sforzo...