Il nostro Andy ha dato solo metà della risposta, sviluppando l'uguaglianza e trovando che poteva essere valida solo se il triangolo era rettangolo.

Tuttavia, le due espressioni, singolarmente, davano entrambe le due risposte.

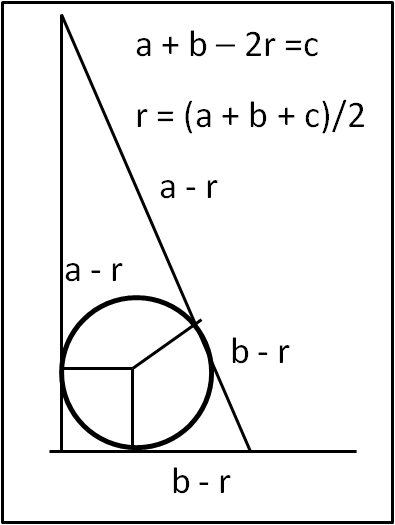
E' facile dimostrare che in un triangolo rettangolo il raggio del cerchio inscritto vale proprio:

r = (a + b - c)/2

Ma è anche facile dimostrare che in un triangolo rettangolo il raggio del cerchio inscritto vale:

r = ab/(a + b + c)

Questa relazione deriva dall'espressione più generale che dice che l'area di un triangolo divisa per il semiperimetro è uguale al raggio r.

Basta dividere il triangolo in tre triangoli che abbiano come base i lati e come altezza proprio il raggio cercato, dato che questo è perpendicolare ai tre lati. Ne segue:

1/2(ar + br + cr)/(a + b + c)/2 = r

Ma se il triangolo è retto, la sua area vale ab/2, ossia:

r = ab/(a + b + c)

La casa verrà costruita nell'incentro del triangolo...