Categorie: Riflessioni
Tags: cento cappelli dieci prigionieri. logica quiz
Scritto da: Vincenzo Zappalà
Commenti:31
NEW: Un re e cento cappelli (con piccola aggiunta)*****
Quiz piuttosto difficile, secondo forse solo a quello degli alieni capricciosi. Mi aspetto la partecipazione dei più bravi (magari non solo loro...)
Il regno di Logicandia sta passando un periodo piuttosto turbolento, con vari gruppi di rivoltosi che vorrebbero eliminare il re, dato che è fin troppo logico e intelligente e non si fa prendere in giro da nessuno. Un ottimo re, insomma, ma -come sempre- il popolo preferisce spesso la mediocrità. Dopo varie battaglie, finalmente, il re riesce ad averla vinta sui rivoltosi e i loro 10 capi vengono imprigionati.
Come già accennato, però, il re è uomo saggio e logico e capisce bene che giustiziando questi rivoltosi non farebbe che soffiare sul fuoco. Meglio essere clementi e cercare di portare dalla sua parte chi lo voleva detronizzare. Offre, perciò, una via di salvezza, basata sulla capacità di trovare una strategia vincente.
Fa portare davanti a sé i dieci prigionieri e gli spiega come potrebbero salvarsi. Davanti a loro vi sono 100 cappelli, tutti uguali, ma di colore diverso a gruppi di 10. Ossia, 10 rossi, dieci blu, dieci viola e via dicendo.
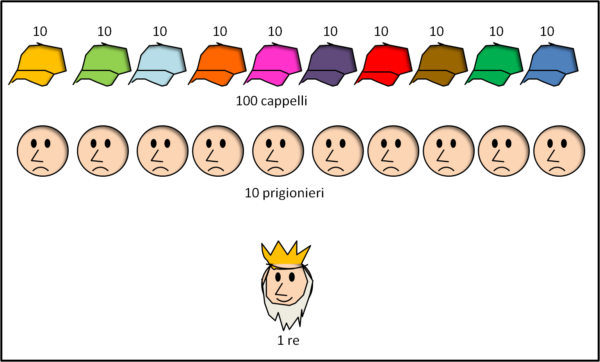
La prova consiste nel mettere sulla testa di ciascuno di loro uno dei cento cappelli, indipendentemente dal colore. Il singolo prigioniero può, quindi, vedere i cappelli di tutti gli altri, ma non il suo e non è possibile fare cenni o proferire parola. Basta che uno solo di loro indovini il proprio cappello per salvare tutti e dieci i prigionieri.
Inoltre, prima di mettere i cappelli al loro posto, i prigionieri li possono analizzare per bene e possono concordare tra di loro la strategia da usare. Senza, alcuna fretta, insomma. Tuttavia, una volta che tutti hanno il cappello in testa, al "via" del re, dovranno dire il colore del proprio cappello TUTTI assieme.
Essendo in Logicandia, i prigionieri riescono a superare la prova e, dopo qualche mormorio, ringraziano il re per avere stuzzicato le loro capacità logiche. Tutto è bene ciò che finisce bene!
Si chiede:
Che strategia devono usare i dieci prigionieri per avere la sicurezza assoluta di essere liberati
SCHEMA TEMPORALE (per non creare confusione aggiuntiva).
1) I prigionieri guardano i cappelli con calma
2) I prigionieri discutono tra loro e decidono la strategia con calma
3) I cappelli vengono messi in testa ai prigionieri. I prigionieri hanno tutto il tempo di guardare bene la situazione ma non possono più parlare
4) Il re dà il via e tutti parlano assieme dicendo SOLO il colore del proprio capello
Spero proprio che non vi siano più fraintendimenti. Il quiz è troppo bello per essere rovinato da soluzioni banali...
31 commenti
Esaminati i colori dei cappelli i prigionieri decidono di assegnare un numero da 1 a 10 ad ogni colore.
Scelgono uno di loro, il prigioniero A, che dovrà essere l'ultimo a dichiarare il colore del proprio cappello.
Scelgono anche altri quattro, B C D E, a cui viene abbinato rispettivamente un particolare numero secondo questo schema:
B = 1 C = 2 D = 4 E = 8
Questi quattro diranno "il mio cappello è giallo" oppure "il mio cappello è blu" ( che sono il primo e l'ultimo colore che vediamo nella figura) Se dicono "Giallo" significa che il loro numero va conteggiato dal prigioniero A , se dicono Blu invece va ignorato.
Gli altri prigionieri sono liberi di dichiarare qualsiasi colore.
Dopo che sono stati messi i cappelli ciascuno vede il cappello di A (tranne ovviamente A).
Il colore del cappello di A corrisponde ad un numero da 1 a 10 che può essere espresso in binario con 4 cifre.
Ad esempio se il colore corrisponde al numero 7 le cifre in binario saranno 1 + 2 +4 che si abbinano ai prigionieri B, C ,D mentre il prigioniero E che rappresenta il numero 8 non entra in gioco.
Quindi i prigionieri coinvolti alla formazione del numero 7, ossia B, C e D diranno di avere un cappello giallo e E dirà di avere un capello blu.
Gli altri potranno dire qualsiasi cosa.
Il prigioniero A somma i numeri "validi": 1 (B), 2(C), 4(D) , ignora il numero abbinato al prigioniero E e dichiara che il colore del suo cappello è il colore che era stato abbinato al numero 7.
La strategia del precedente commento si basa sulla ipotesi che i prigionieri possano parlare nella sequenza di loro scelta. Nel testo non si dice nulla che vieti questa possibilità.
Tuttavia, nel caso che i prigionieri non possano scegliere in quale ordine parlare ma vengano interrogati sul colore del loro cappello in un ordine deciso casualmente dal re, potrebbe succedere che il prigioniero A sia interrogato per primo o comunque prima di avere sentito tutti gli altri "informatori" B,C,D,E.
In questo modo, non possedendo una informazione valida, dovrebbe tirare a indovinare con solo il 10% di probabilità a suo favore e la strategia fallirebbe in quanto viene a cadere la certezza del risultato favorevole.
Data questa ipotesi, i prigionieri dovranno organizzarsi diversamente, nel modo seguente:
Il gruppo si riunisce e concorda con precisione i colori dei cappelli ( questo è necessario perché potrebbe esserci un daltonico e occorre avere la certezza che anche lui dichiari i colori con il giusto nome).
Poi vengono formati due gruppi: A e B , di 5 persone ciascuno e si stabiliscono cinque abbinamenti in modo che a ciascun individuo nel primo gruppo corrisponda un partner nel secondo gruppo.
Il prigionero A1 , del gruppo A sarà "gemellato" con B1 del gruppo B e così via.
Quando verrà interrogato A1 dirà: "il mio cappello è di colore x " comunicando in realtà al partner B1 che ha visto che il suo cappello ha quel colore.
Analogamente, se sarà B1 a dover rispondere per primo , dichiarerà di avere un cappello del colore che in realtà è quello del cappello indossato da A1. In questo modo A1 saprà cosa rispondere quando sarà il suo turno.
In qualsiasi ordine vengano interrogati i prigionieri, nel caso meno favorevole, dopo la quinta dichiarazione, gli altri 5 rimasti avranno ricevuto tutti l'informazione sul colore del loro cappello e quindi potranno dare la risposta corretta che consente di salvare tutti.
Naturalmente questa strategia è valida anche se i prigionieri possono scegliere l'ordine in cui parlare. Addirittura, nel momento stesso in cui parla il primo, il suo partner è già in grado di dare la risposta giusta e con solo due dichiarazioni il gioco è fatto.
Mi dispiace Mau, ma avevo dimenticato di dire una cosa fondamentale: I prigionieri devono dire il colore del proprio cappello tutti assieme. Non si può agire sul tempo delle varie risposte. Sarebbe troppo facile...
Essi hanno il tempo di guardarsi tra di loro per qualche minuto, ma in perfetto silenzio e senza mosse strane. Poi il re dà il via e ognuno devr parlare immediatamente.
Abbiate pazienza, ma dimentico sempre qualche pezzetto...
D'altra parte, la strategia basata su tempi diversi è piuttosto banale, troppo...
Se A1 comunica a B1 il colore del suo cappello, B1 potrà dire sicuramente il giusto colore! Nel caso che B1 parli per primo, il ruolo si inverte... No, Logiclandia è una nazione decisamente più sofisticata
La banalità del caso in cui i prigionieri possano parlare in tempi diversi si nota molto bene se consideriamo solo due prigionieri. Il primo che viene invitato a parlare deve dire il colore dell'altro. Il secondo ha, quindi, l'informazione necessaria. Un re davvero sciocco, direi ...
Infatti mi sembrava di una facilità estrema e del tutto incoerente con i 5 asterischi.
Ora non mi ci posso dedicare ma spero in serata di trovare un po' di tempo per qualche ragionamento.
Vorrei fare una riflessione riguardo ai nuovi quiz...
Avendo deciso di limitarmi a quelli piuttosto complicati che, spesso, vedono sempre un piccolo manipolo di "fedeli", devo rendermi conto dei rischi dell'"informazione mancante". In poche parole, qualcosa di importante per il quadro completo, viene considerata come "ovvia", anche se tale non è. In questo caso, l'informazione fondamentale era la simultaneità della risposta che cambia completamente la difficoltà. Sarà che sto rimbambendomi sempre più, ma anche leggendo e rileggendo, qualcosa scappa sempre.
A riguardo, devo ringraziare il grande Mau che riesce sempre a evidenziare i punti "critici". Il che però comporta correzioni al testo e, magari, la perdita di pazienza da parte dei solutori più che abili. Questo mi dispiace molto, dato che questo quiz è veramente un bell'esempio di logica che sembrerebbe anche inaspettata. Vi prego ci cercare di rileggerlo con attenzione, dato che svela un piccolo mondo segreto nei meandri delle probabilità.
La soluzione completa richiede un certo impegno. Mi limito ad esporre qui alcune considerazioni che potrebbero risultare utili.
il caso più elementare: è quello di due giocatori A e B e di due set di cappelli di colori C1 e C2.
A vede il colore del cappello di B ma non può dedurre in alcun modo il colore del proprio. La stessa cosa vale per il giocatore B. Ciascuno ha il 50% di probabilità di indovinare il colore del proprio cappello.
La probabilità che almeno uno di loro due indovini è P= 1- la probabilità che sbaglino ambedue.
La probabilità che sbaglino ambedue è 0,5*0,5 = 0,25 Quindi la probabilità di avere almeno un risultato giusto vale 1-0,25 = 0,75 Non vedo strategie che possano migliorare questo risultato
Passiamo al caso successivo: tre giocatori A B C con i corrispondenti set di cappelli di colore C1 C2 C3
La scelta casuale della risposta comporta per ciascuno la probabilità di errore di 2/3. Quindi la composizione degli errori vale 2/3 ^3 = 0,296 e la probabilità di almeno una risposta corretta vale
P = 1 – 0,296 = 0,7037 peggiore di quella che abbiamo visto per 2 giocatori.
Ma questo risultato può essere migliorato.
Nel caso che A B C indossino cappelli di un medesimo colore, ciascuno di loro vedrà due cappelli uguali.
Nel loro incontro preliminare potrebbero avere concordato che se si vedono 2 cappelli del medesimo colore conviene dichiarare di indossare quel colore. Infatti se tutti osservano questa regola saranno almeno in due ad avere risposto correttamente. Dato che i colori sono 3 questo caso si può presentare 3 volte.
Nella configurazione in cui ci siano solo due ( e non tre) cappelli del medesimo colore uno dei tre prigionieri li vedrà ambedue mentre gli altri prigionieri vedranno cappelli di due colori diversi.
Il prigioniero che vede i due cappelli uguali attuerà la strategia concordata e dichiarerà (sbagliando) di indossare il colore che vede; gli altri due giocatori, che vedono due colori diversi, sono proprio quelli che hanno il cappello del medesimo colore.
Dovranno dire “contemporaneamente” uno dei due colori che vedono, ma per essere certi di citare ambedue i colori dovranno essersi accordati in precedenza, codificando i colori C1 C2 C3 in base al loro numero.
Avranno ad esempio stabilito che A sceglierà di dire il colore con indice più piccolo e B quello con indice più grande. In questo modo uno dei due dichiarerà il colore corretto del proprio cappello.
Le possibili combinazioni di colori coppia+singolo , avendo tre colori, sono sei. Ma non tutte portano al risultato vincente perché se la strategia che consente ai giocatori A e B di indicare colori diversi può essere replicata anche alla combinazione dei giocatori A e C ( A dichiara sempre il colore di indice minore e C quello di indice maggiore), quando si trovano a confronto B e C ambedue sceglieranno il colore di indice maggiore e la metà delle volte mancheranno l'obiettivo.
Sui sei casi che si possono presentare solo 5 avranno successo mentre l'ultimo fallirà il 50% delle volte.
Resta l'ultima configurazione quella in cui i colori dei cappelli sono tutti diversi e ciascun giocatore vedrà due colori diversi. Potrà legittimamente pensare di trovarsi in uno dei sei casi appena visti e agire di conseguenza con il risultato, però, di sbagliare sempre.
Sui 10 casi di cui abbiamo parlato, l'obiettivo è conseguito 8,5 volte quindi il miglioramento della probabilità di successo dovuto alla strategia messa in campo si è realizzato.
Tornando alla situazione dei 10 prigionieri : il numero di possibili configurazioni cresce vertiginosamente. Se i prigionieri sono 10 e i cappelli sono 10 ogni prigioniero, tirando a indovinare, ha una probabilità di sbagliare di 9/10.
la probabilità che tutti sbaglino nel dichiarare il colore del proprio cappello è quindi 9/10 ^10 = 0, 349
Quindi la probabilità di avere almeno un risultato giusto, rispondendo a caso, è 1- 0,349 = 0,651
Si parte da questo valore base per costruire delle regole nelle risposte da dare che consentano di migliorare la probabilità complessiva
Uno dei criteri è quello di considerare la presenza del "colore dominante" , inteso come quel colore di cappello che, dal punto di vista degli osservatori, compare almeno una volta in più di ogni altro colore tra i 9 cappelli che vedono.
Ad esempio, una possibile configurazione decisa dal re può essere 3 cappelli rossi e 7 di diversi colori, uno per tipo.
La visione di coloro che non hanno il cappello rosso ( sono 7 persone) è di 3 cappelli rossi + altri 6 di colori diversi, mentre quelli (3 persone) che hanno i cappelli rossi vedranno solo 2 cappelli rossi e 7 di altri colori diversi.
Il colore dominante è quindi il rosso dal punto di vista di tutti. Se tutti citano questo colore, allora i tre che lo indossano avranno indovinato.
Tuttavia le configurazioni non si presentano sempre con un colore dominante in modo così evidente agli occhi di tutti gli osservatori, come abbiamo visto nel semplice esempio di tre giocatori nascono situazioni ambigue che vanno gestite con un raffinamento della strategia. ( o trovandone una più potente e generalizzata)
L'argomento merita certo un approccio più rigoroso e ordinato di queste semplici considerazioni . Mi resta però una domanda, Enzo, sul fatto che nell'ultimo tuo commento accenni alla probabilità mentre il quiz richiede che venga raggiunta la certezza del risultato.
La certezza implica una probabilità del 100%. E' questo l'obiettivo?
Intendevo probabilità in senso generico. Ovviamente, nel nostro caso, la probabilità deve arrivare al 100%.
In generale, però, sconsiglio di fare una trattazione probabilistica con tanto di formule. Basta il ragionamento e molta logica.
Consiglio di porre attenzione alla richiesta del re: "basta che uno risponda esattamente" e quella fatta a voi: "la sicurezza di essere liberati". Due frasi equivalenti, ma qualcosa potrebbe nascondersi dietro e renderle anche abbastanza diverse, anche se il risultato è lo stezzo.
Caro Mau,
ho riletto con attenzione il tuo commento.
Beh... posso dirti che una delle conclusioni, che tu dai per certa, è SBAGLIATA. Il ragionamento che porta allo sbaglio, è proprio quello che allontana dalla giusta strategia. Ricordiamoci che la somma di dieci 10% porta al 100%, sempre che capiti qualcosa di fondamentale...
Grazie, è un indizio importante che dovrò elaborare appena possibile.
Provo con 9, con 10 non cambia.
123456789
223456789
333456789
444456789
555556789
666666789
777777789
888888889
999999999
Cosa si intende per “guardare bene la situazione”. Nell’ultimo caso tutti 9 possono vedere i cappelli rimasti? Contare quelli rimasti?
Hai proprio ragione, sono stato troppo pessimista quando, parlando del caso dei due giocatori A e B e delle 2 coppie di cappelli di colore C1 e C2, ho scritto che non si può fare nulla per ottenere un risultato migliore di quel 75 % che si ottiene con risposte casuali.
Mi torna in mente un vecchio esempio che voglio citare qui. Alle porte di una città ci sono due strade, una porta all'abitato, l'altra porta alle paludi. Proprio al bivio ci sono due sfaccendati , uno dice sempre la verità e l'altro dice solo bugie. Non essendoci alcun cartello segnaletico, i turisti sono costretti a chiedere informazioni a uno dei due perdigiorno, ma non sanno quale dei due sia il mentitore perciò, qualsiasi domanda pongano all'uno o all'altro, non sapranno mai se la risposta sarà il vero o il falso. Però una domanda che risolve il problema esiste e può essere posta indifferentemente all'uno o all'altro.
La domanda è ... "se chiedessi al tuo amico quale strada porta in città cosa risponderebbe? "
Se ho parlato con il sincero mi dirà che l'altro direbbe la strada x (ma sarebbe falso perché il sincero dice la verità e riporta la falsità dell'altro. ( vero*falso = falso)
Se invece ho parlato con il bugiardo negherà la risposta (veritiera) dell'altro e quindi avrò comunque una bugia perché ( falso*vero = falso).
Insomma, per arrivare in centro dovrò prendere la strada opposta a quella che mi verrà detta.
La domanda posta produceva una "combinazione" delle risposte e solo così ho avuto un risultato utilizzabile.
Allora, tornando al caso elementare dei due giocatori, la loro strategia dovrà essere "coordinata" e non individuale.
Dovranno presidiare tutti i casi possibili dividendosi i compiti, ossia realizzare congiuntamente l'esplorazione "completa" spazio delle possibilità.
Le possibilità, in definitiva, sono solo due: indossiamo cappelli uguali oppure indossiamo cappelli diversi.
A potrà scegliere di presidiare il caso "cappelli uguali" e B si occuperà del caso "cappelli diversi". Ma in che modo?
Quando A osserva il cappello di B fa scattare il suo pregiudizio: I cappelli sono uguali, quindi sto vedendo una copia del mio cappello, dichiaro lo stesso colore che vedo.
Contemporaneamente B osserva A e il suo "pregiudizio" gli suggerisce: questo cappello che vedo è diverso dal mio, quindi dico che il mio è dell'altro colore.
Siamo sicuri che uno avrà ragione e l'altro avrà torto perché o i cappelli sono uguali o sono diversi e non esiste altra possibilità. Quindi uno dei due avrà "indovinato" e saranno liberi entrambi.
Ma dire "indovinato" non è corretto perché ha solo occupato lo spazio delle possibilità nel modo preventivato dalla strategia, con la sicurezza che il compagno stava presidiando l'altra metà dello spazio.
Questo mi sembra un notevole passo avanti: la strategia deve coprire tutto il campo con N "perdenti" e un solo "vincitore" tipo Highlander ... ne resterà solo uno.
Ora il problema è di trasportare questa logica nello scenario dei 10 giocatori e relativi cappelli colorati. Credo che il fatto che siano 10 non abbia nulla di magico, potrebbero essere anche 8 oppure 12. La difficoltà è di capire come codificare i diversi cappelli colorati e distribuire le responsabilità, come in una squadra sportiva dove ciascun elemento svolge un proprio ruolo.
Ma come si dice in quel famoso film... ci penserò domani.
Scusa Gianfranco,
ma si chiede la strategia necessaria, non qualche possibile caso. Tutti i possibili casi devono portare alla salvezza.
Guardare con attenzione vuol dire "ricavare qualcosa di utile per eseguire l'azione vincente"
Ottimo Mau...
Non voglio ancora dare aiuti, ma la strada è quella giusta. L'esempio di due prigionieri aiuta molto nello stabilire il concetto fondamentale, ma deve essere generalizzata...
Ancora qualche ragionamento sulla configurazione a due...
Lo spazio delle possibilità è costituito da quattro configurazioni che possiamo rappresentare in
binario con 0 e 1 e nel corrispondente decimale
00 0 fa parte della “zona” di A
01 1 “ B
10 2 “ B
11 3 “ A
Possiamo dire che mentre A si occupa delle due configurazioni 00 e 11, B si occupa delle altre due: 01 e 10. Metà campo per ciascuno.
Quando A vede il valore 0 di B (il cappello del primo colore C1) deve “giocare nella sua zona”, cioè fare in modo che la combinazione complessiva sia 0 0 .
Aggiunge il suo 0 con la sua dichiarazione di avere un cappello del colore C1 (come B).
Quando vede il valore 1 di B (il cappello del secondo colore C2) deve “aggiungere” 1 per avere la combinazione 11 di sua competenza , il che equivale a dichiarare di avere un cappello del colore C2.
Per B vale il discorso opposto. Quando vede che A indossa 0 ( colore C1) aggiunge il suo 1, cioè dichiara che il suo cappello è di colore C2. Quando invece A indossa 1 (colore C2) allora B aggiunge il suo 0, cioè dichiara che il suo cappello è di colore C1.
-------------------------------------------
Proseguendo nella analisi critica del mio primo commento del 26 maggio, riprendo ora in esame il caso di 3 giocatori A B C, un passo avanti verso la generalizzazione.
Lasciamo da parte il discorso della probabilità che almeno uno dei tre indovini il colore del proprio cappello, dichiarandolo "a caso" o con un ragionamento individuale. Non è questa la nostra strategia.
Concentriamoci invece sul nostro scopo: quello di coprire tutto il campo delle possibilità dividendolo in “Zone” e facendolo presidiare totalmente dai tre giocatori (organizzati appunto “a zona”) . Proprio come abbiamo già fatto nel caso di due soli giocatori.
Ma quanto è esteso questa volta il campo delle possibili configurazioni? Avendo 3 giocatori A,B,C e tre colori C1 ,C2, C3 ne avremo ben 27. Non fatemele scrivere tutte e 27, ma accontentatevi delle prime 9 ( le altre, volendo, le potete ricavare mettendo al primo posto 1 e 2 )
Eccole qui …
Per poter maneggiare la base 3 (i cui simboli classici sono 0, 1, 2) introduco queste associazioni con i tre possibili colori dei cappelli C1, C2, C3 : C1 = 0 C2 = 1 C3 = 2
in base 3 in base 10 Zona di A Zona di B Zona di C
000 0 SI
001 1 SI
002 2 SI
010 3 SI
011 4 SI
012 5 SI
020 6 SI
021 7 SI
022 8 SI
e così via fino all'ultima delle 27 configurazioni.
In modo più sintetico possiamo dire che abbiamo creato tre partizioni assegnando la responsabilità dei numeri multipli di 3 ad A, quella dei multipli di 3 +1 a B e quella dei multipli di 3 + 2 a C
Non ci sono altre possibilità.
Ma come agiranno i giocatori? Ossia, con quale criterio arriveranno a stabilire il colore da dichiarare?
Ebbene, agiranno tutti nello stesso modo.
Dovranno osservare i cappelli degli altri e valutare se il numero che si ottiene sommando i corrispondenti valori “cade nella loro zona” Se così risulta, non modificheranno quel totale, assegnandosi un cappello di valore nullo, altrimenti si assegneranno un cappello il cui valore fa cadere il totale nella loro zona. Questo corrisponde a presidiare un terzo delle configurazioni.
Agendo tutti in questo modo terranno sotto controllo il 100% dei casi possibili. Uno solo di loro indovinerà mentre gli altri due, ovviamente, sbaglieranno
Facciamo un esempio: il re decide di assegnare i tre cappelli in questo modo:
Per A un cappello C2, per B un cappello C2, per C un cappello C3.
Sappiamo che ciascun giocatore vede solo 2 cappelli, quelli degli altri.
A vede che B ha un cappello color C2 (che vale 1) e C ha un cappello color C3 (che vale 2). Insieme il valore che accumulano vale 1 + 2 = 3. Dato che A presidia i multipli di 3 non dovrà alterare questo risultato e quindi si assegnerà e dichiarerà un cappello del valore = 0 (colore C1).
E' sbagliato ma non importa, quello che conta è che ha presidiato un terzo dello spazio delle configurazioni.
Anche B farà questa stessa operazione. Prima controlla i valori associati ai cappelli degli altri due giocatori, poi fa una dichiarazione del proprio colore in modo da controllare il gioco nella sua zona.
Vede che A ha in testa un cappello C2 (che vale 1) e che B ha un cappello C3 (che vale 2).
Esegue la somma 1 + 2 = 3. Non è nella sua zona ( lui governa i multipli di 3 + 1). Per garantire il controllo della sua zona dovrà dichiarare un cappello C2 (che vale 1) così avrà allineato il totale a un multiplo di 3 +1. Sia noi che il Re ci accorgiamo che, dichiarando un cappello color C2, il giocatore B ha “indovinato” e si potrebbe già festeggiare, ma vediamo cosa succede con l'ultimo giocatore. Spero che prevediate fin da ora che non indovinerà il colore del suo cappello.
Il giocatore C farà le sue osservazioni e vedrà che il cappello di B è C2 (vale 1) e anche quello di A è C2 (e vale 1). Fa la somma e trova un totale di 2 . Si tratta di un numero della sua zona, un multiplo di 3 +2. Allora dovrà semplicemente dichiarare di avere un cappello che vale 0, ossia un cappello di colore C1.
Sappiamo che non è così, e questo ci rallegra perché è la garanzia che nulla è sfuggito al controllo.
Ora , se avete capito questo diabolico meccanismo, vi lascio il week end per provare a correggere l'ultima parte del mio vetusto commento del 26 maggio, applicando il metodo al caso proposto dal quiz dei 10 prigionieri. Confido che non avrete difficoltà con la base decimale.
Ricordate: uno solo deve “indovinare” e tutti gli altri devono sbagliare.
Cerchiamo di riassumere nel modo più semplice possibile la situazione...
Affinché si possa sfruttare tutto il 10% di ogni singolo prigioniero NON deve esserci alcuna sovrapposizione della risposta di uno con quella di un altro. Ciò implica che è fondamentale che uno e uno solo dica il colore giusto. Il che vuole anche dire che ognuno ha solo bisogno di essere sicuro che nessun altro segua la sua strategia. In tal modo se parlano in 10, uno e uno solo dice SICURAMENTE il proprio colore. Lui sa esattamente che quello che ha detto ha solo una probabilità su 10 di essere giusto, ma quello che conta è che sicuramente uno dei 10 è "costretto" a dare la risposta giusta.
Mau è vicino alla soluzione... forse deve cercare di generalizzare la procedura rendendola però di semplice e rapida applicazione. In questo contesto il fatto di avere 10 prigionieri è di grande aiuto (aiuto fondamentale...). Consiglio, perciò, di utilizzare proprio 10 per delineare la strategia e poi, magari, applicarla a qualche caso numerico...
In poche parole, rendiamo semplice la descrizione della procedura!
Se i giocatori sono 10 ogni zona sarà un decimo di tutto lo spazio delle possibilità.
La somma dei valori dei 9 cappelli (quelli che ciascuno riesce a vedere) vale come minimo zero e come massimo 90.
Il giocatore A presidia lo zero, il 10 il 20, etc.. Insomma tutti i multipli di 10. Se il totale dei valori che vede vale un multiplo di 10, dichiara il colore C1 che vale 0 , altrimenti aggiunge quanto basta per allinearsi al successivo multiplo di 10 e dichiara conseguentemente il colore corrispondente al valore aggiunto
Se il totale che vede fosse per esempio 37, avrebbe come resto 7. Allora calcolerà il complemento di 7 a 10, che vale 3 e si assegnerà il cappello del colore che vale 3 ossia il cappello di colore C4.
La zona di B è quella dei multipli di 10 +1.
Anche B divide il totale per 10 e ottiene un resto. Calcola il complemento a 1o e somma la sua "costante di zona, che vale 1 ( quella di A valeva 0) infine B associa il valore del risultato al colore corrispondente e fa la sua dichiarazione
Tutti gli altri agiranno in modo simile nell'ambito della propria zona. Calcolano il totale , dividono per 10, trovano il resto , aggiungono la costante della loro zona , associano il risultato al colore del cappello e fanno la loro dichiarazione
Mi sembra che funzioni e spero che sia abbastanza chiaro per tutti .
Facciamo un esempio finale.
Il re assegna i dieci cappelli come segue Qui sotto le elaborazioni dei giocatori
Giocatore colore valore ******* conteggio resto compl. 10 cost. zona valore colore dichiarato
A C1 0 ******* 28 8 2 0 2 C3
B C3 2 ******* 26 6 4 1 5 C6
C C2 1 ******* 27 7 3 2 5 C6
D C1 0 ******* 28 8 2 3 5 C6
E C8 7 ******* 21 1 9 4 3 (da 13) C4
F C5 4 ******* 24 4 6 5 1 (da 11) C2
G C3 2 ******* 26 6 4 6 0 (da 10) C1
H C8 7 ******* 21 1 9 7 6 (da 16) C7
I C1 0 ******* 28 8 2 8 0 (da 10) C1 !!!
L C6 5 ******* 23 3 7 9 6 (da 16) C2
Come si vede, indovina solo il giocatore contrassegnato dalla lettera I mentre tutti gli altri sbagliano.
Magari qualcuno (Gianfranco?) può provare a fare qualche altro esempio per confermare che, procedendo con questa logica, si ottiene regolarmente un solo vincitore.
Per una leggibilità decente riscrivo i dati dentro una tabella (come si dovrebbe fare sempre
Assegnazioni del Re Elaborazioni dei giocatori
dichiarato
Adesso sì che ci siamo! Molto bene Mau. Ogni prigioniero sceglie a priori un valore del "resto". In tal modo tutti i prigionieri avranno un codice diverso, da 0 a 9 (che sono tutti i possibili resti!). Si disinteressa completamente del suo risultato, ma svolge il proprio ruolo di "pedina" che deve compiere un'azione diversa da quella di tutti gli altri, ossia imporsi il codice di resto uguale a zero. Essendo l'unico a farlo sfrutterà tutto il suo 10% di possibilità e non avrà nessuna possibile sovrapposizione con altri risultati. Lo stesso discorso vale per tutti gli altri, ognuno con un codice diverso. In tal modo uno e uno solo darà la risposta giusta relativamente al suo codice "resto".
Il fatto di avere dieci prigionieri è utilizzato per semplificare la descrizione, in quanto il resto della divisione per 10 è l'ultima cifra della somma dei cappelli. Niente cambia usando basi diverse e, quindi, anche quella binaria.
Per fare alcune prove, anche in casi particolari, come tutti i cappelli uguali o tutti diversi, è bene crearsi uno schema di questo tipo
P =Prigioniero
R = resto imposto SP = somma parziale ST = somma totale se il suo resto fosse giusto D = differenza, ossia cappello che ha in testa...
P R SP ST D (ST - SP)
A 0 43 50 50 - 43 = 7
Il prigioniero, deciso come A, si impone come resto o. Questa parte è stata decisa coralmente. Il prigioniero vede come somma parziale dei cappelli 43. Lui si è imposto di avere come resto 0, il che vuol dire che la somma totale deve finire per 0 (divisione per 10 esatta, con resto 0). La differenza tra la somma totale calcolata e quella parziale che riesce a vedere è pari a 8. Il prigioniero esclama perciò 8 come colore del suo cappello!
E via dicendo...
Ovviamente, a ogni colore di cappello è stato dato un numero diverso, da 0 a 9.
Notiamo come la strategia generale sia una sola, ma le azioni da eseguire mentalmente da ogni prigioniero siano matematicamente tutte diverse, dato che diverso è il resto che ognuno si impone. Notiamo anche come poco importi che due o più prigionieri vedano la stessa somma parziale, La loro azione è comunque diversa, dato che cambia il resto.
Provate per credere!
Due cappelli 1,2, quattro possibilità
11
22
12
21
a dice uguale b , b dice diverso a
a1 b2
a2 b1
a2 b2
a1 b1
Appena terminato con impegni vari, provo “guardare bene la situazione” con 10 capelli.
Benissimo Gianfranco, vedrai che i conti ti torneranno.
bravo Gianfranco! chi ben inizia...
Se poi volete giocherellare con le varie possibili assegnazioni di cappelli e le conseguenti previsioni dei prigionieri, potete andare a questo link
dove troverete un semplice foglio excel in cui immettere (nella colonna gialla) i valori dei colori (da 0 a 9 ) che il re ha assegnato a ciascun prigioniero/giocatore e ottenere le dichiarazioni di ciascuno sul proprio colore, constatando che esiste un solo vincitore.
Se provate a modificare anche uno solo dei colori vedrete cambiare la situazione delle risposte e individuerete il nuovo vincitore.
La pagina excel, eseguibile anche online con l'applicazione fogli google, senza doverla necessariamente scaricare, ha questo aspetto e realizza il calcolo basato sulle semplici formule di cui abbiamo parlato nei commenti.
Grande Maurizio!
Avevo preparato un foglio Excel simile, ma mi hai preceduto. Praticamente la posizione del prigioniero determina il valore da dichiarare e, come ha scritto Enzo, la probabilità dei singoli 10% sommati determina una probabilità del 100% nella risposta di uno solo dei prigionieri.
Allego il link del foglio Excel, modificabile se si possiede un account Google (sennò purtroppo solo visualizzabile), e mi limito ad una breve descrizione:
https://docs.google.com/spreadsheets/d/1KP3Uzbi3237A1pYM0yvK76QJ9YjvFrO5/edit?usp=sharing&ouid=111281464294582462084&rtpof=true&sd=true
Nella tabella superiore, per la colonna B i prigionieri numerati da 1 a 10, nella colonna C il colore del berretto associato ad un numero generato casualmente tra 0 e 9 per ogni cella, nella cella con sfondo blu e caratteri gialli la somma totale dei 10 cappelli, nella colonna D la somma parziale che vede ciascuno prigioniero sommando i numeri dei berretti degli altri 9(che è la somma totale meno il numero del proprio berretto), nella colonna E il resto della divisione per 10 di ogni singola somma parziale, nella colonna F il complemento a 10 del valore scritto nella colonna precedente, nella colonna G la posizione occupata da ciascun prigioniero numerata da 0 a 9 (i prigionieri possono disporsi sui vertici di un decagono e, scelto il riferimento 0, si ottengono le posizioni successive), nella colonna H il numero dichiarato da ciascun prigioniero sul riferimento della colonna F (ad esempio per il prigioniero 10, i suoi valori da sommare sono 9+9=18, considera solo le unità quindi 8, il prigioniero 9 somma 4+8=12 quindi 2 unità, e così via), la colonna I verifica che una sola risposta sia corretta.
La tabella inferiore è del tutto simile con la differenza che genera un numero random tra 0 e 9 uguale per tutti i prigionieri, cioè tutti indossano un cappello dello stesso colore.
Per chi avesse curiosità di scaricare il file, selezionata la cella rossa, ad ogni pressione del tasto CANC, vengono generati automaticamente e in maniera random i numeri tra 0 e 9 associati ai cappelli nella 1a tabella, mentre nella seconda il numero random viene assegnato al 1° prigioniero e successivamente lo stesso numero a tutti gli altri.
Mi piace questa idea della generazione dei numeri random.
Bravo Andy!
Certo, Andy, che se i prigionieri fossero stati 7 e i colori fossero stati 7, pur mantenendo la stessa logica avremmo avuto qualche difficoltà in più a fare i conti. Anche i nostri fogli excel avrebbero dovuto essere opportunamente modificati. Giusto?
Pensaci un po' ...
Caro Maurizio,
nel caso di 7 prigionieri con a disposizione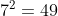
cappelli di 7 colori differenti la logica rimane uguale, l'unica difficoltà (facilmente superabile) è la conversione da base 10 a base 7 della colonna "Dichiarazione";
uno screenshot di 4 griglie che lavorano in contemporanea spiega tutto:
Praticamente ho aggiunto una colonna alla destra dei valori in base 10 per convertirli in base 7, sempre con il criterio che se il numero convertito è formato da una "settina" + n unità, scarto la "settina" e immetto solo il valore dell'unità (che ovviamente in base 7 viaggia da 0 a 6).
Il calcolo del valore dichiarato è ancora più semplice di quanto ho scritto prima: basta sommare il complemento a 7 con la posizione e, se si ottiene un valore maggiore o uguale a 7 , si sottrae 7;
in generale con
prigionieri ed 
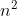cappelli la logica è sempre la stessa:
si numerano i cappelli secondo gli
colori da 
a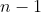 
,
dalla somma che ciascun prigioniero calcola sui restanti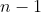
cappelli, si procede con il calcolo del resto della divisione per 
,
il risultato ottenuto si complementa ad
,
si fissano le posizioni assunte dai prigionieri da
a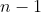 
,
si denominano con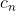
l'ennesimo complemento a 
e con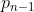 
la posizione ennesima,
la relativa dichiarazione è la somma dei due: valore dichiarato =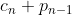
se tale valore è maggiore o uguale ad
, il dichiarato sarà uguale a &space;-&space;n)
Un esempio con n=20 prigionieri e 20 cappelli di 20 colori differenti (20×20=400 cappelli):
Caro Andy, mi aspettavo questa bella generalizzazione ( essendo in viaggio ho dovuto limitarmi alla base 7 e rinunciare alla base 12 che avevo in mente.
Ora direi che possiamo fermarci. Se dovessero prenderci prigionieri ne vedranno delle belle.
Che dire? Tutto bene, ma sono convinto che senza excel si possa fare benissimo a "mano libera": basta un foglio, una matita e saper fare differenze e somme. Non credo sia chiedere troppo al futuro dell'umanità. Temo che Asimov l'avesse vista perfettamente bene... Non saremo mai schiavi delle macchine come dice certa fantascienza squallida e cruenta, ma siamo già abbastanza servili verso di loro per un futuro privo di basi e di capacità che ci obbligheranno sempre più a nascondere. Spero che questo blog serva a ritardare un poco un momento ormai segnato nell'evoluzione umana. Pardon... "depravazione" umana. Forse la Terra ha già scelto il nostro successore: l'insetto...