L'aritmetica dei Krull ***
L'aritmetica dei Krull è inserita in Matematica e Geometria
Nella Grande Enciclopedia Galattica i Krull sono citati come la seconda civiltà più intelligente del cosmo, subito dopo i Terrestri.
I Krull abitano in una galassia poco visibile che invece di due braccia ne ha uno solo.
Forse proprio per questo anche loro hanno un braccio solo, con una sola mano di 7 dita. Nell'aspetto ricordano un po' Quazel che forse alcuni di voi ricordano, ma lui aveva due mani con 4 dita ciascuna.
Naturalmente ad ogni dito dei Krull corrisponde un nome, brevissimo, non come i nostri pollice indice medio anulare e mignolo, che non sono per niente nomi pratici e che, se dovessimo estenderli con altri due, non si sa proprio quali nomi ci dovremmo inventare. No, i nomi delle dita krulliane sono un trionfo della semplicità: a b c d e f g.

Le bambine e i bambini krull imparano a contare appena nati, in apposite scuole per l'infanzia.
il primo insegnamento riguarda la moltiplicazione (pensavate fosse la somma, vero?) Invece no.
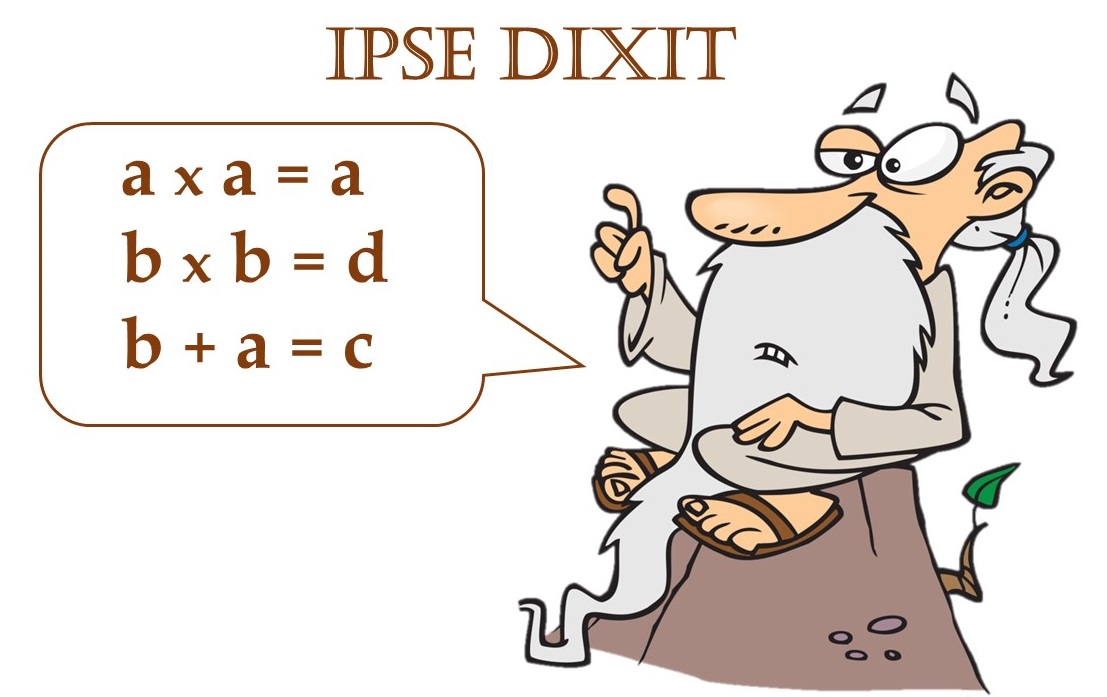
Prima di tutto si deve capire che a per a = a
A questo punto c'è sempre qualche bambina (sono le più attente) che chiede: allora b per b = b?
il maestro alza gli occhi al cielo (sarà la millesima volta che sente questa domanda) e risponde NO, non fa b ma un’altra cosa che vi dirò tra poco.
Ma perchè non fa b? Chiede un bambino.
Perché lo ha detto Aristot, un filosofo krulliano vissuto 2000 anni fa, ipse dixit.
Ma cosa c'entrano pixi e dixi? Chiede un terzo bambino fanatico dei cartoni animati di Hanna e Barbera.
Il maestro fa finta di niente e prosegue la lezione.
Per oggi mi basterebbe farvi capire questa cosa che vi dico.
a x a = a a x b =b a x c = c
Ok, fa la prima bambina, basta così. Generalizzando direi cha “a x qualcosa” fa sempre qualcosa, cioé quel qualcosa li. Tutti gli altri applaudono picchiando la mano sul banco.
Allora, se questo e chiaro a tutti, possiamo proseguire. Qualcuno vuol provare a dire cosa fa bxb? Abbiamo già detto che secondo Aristot non fa b, ma farà pure qualcosa, no?
Farà ancora a! Grida uno dall'ultimo banco.
Ma figuriamoci se può fare a, sbotta un altro, farà certo più di a e anche più di b forse c o addirittura d.
Bravo! fa proprio d.
ma perche è così sicuro che faccia d, signor maestro? Chiedono in molti (i krulliani non usano dare del tu ai maestri o chiamarli con il nome di battesimo).
Ipse dixit, care mie e cari miei, ipse dixit.
(Noterete come i maestri krulliani siano attenti alle regole antidiscriminatorie sul genere)
Ma, a parte pixi e dixi, non c'è uno straccio di dimostrazione che bxb faccia proprio d e solo d? Possibile che in 2000 anni nessuno abbia trovato una giustificazione piccola a piacere per non lasciare dubbi?
La domanda l'ha fatta un ripetente, molto polemico.
In effetti qualche anno fa due matematici hanno trovato, indipendentemente, una specie di dimostrazione, ma per capirla dobbiamo prima studiare le somme.
E cosa sono le somme?
Ecco, invece di dire “per”... si deve dire “più”.
Tutto qui? Credevo fosse una cosa più difficile.
No, basta dire più e, ovviamente, sapere cosa ne pensa Aristot riguardo al risultato.
Ah già, e cosa ne pensa?
Secondo lui, per esempio, a più a dovrebbe fare b.
OK, salta su la solita bambina allora, generalizzando possiamo dire che un dito più a fa il dito dopo quindi b + a fa c, e c più a fa d, e così via.
Questo è proprio quello che pensa anche Aristot.
Ma quando faccio g + a che dito devo dire come risultato? Mica ho altre mani per andare avanti, cosa faccio? Torno da capo e dico il primo dito? dico a?
Sí e no. Devi anche dire che hai finito la mano. Cosí dirai che il risultato è “a mani” e “a dita”. Chiaro?
Mica tanto.
Capirai più avanti, facendo le esercitazioni a casa. Magari ti fai aiutare dai tuoi fratelli più grandi o dai tuoi genitori.
Intanto, visto che l'orologio segna quasi l'a, chiudiamo qui la lezione. Per questo pomeriggio vi do da studiare sul libro di testo da pagina a fino a pagina d compresa.
(continua... forse)






4 commenti
Ma allora, caro Maurizio, i Krull dovrebbero adottare un sistema di numerazione "settale" o "g-ale",
per cui, correggimi se sbaglio,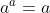 ,
, 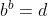 ,
, 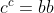 .
.
Se non ricordo male, una delle civiltà del Centro e Sud America, pare adottasse un sistema di numerazione a base 20, considerando le 10 dita delle mani + le 10 dita dei piedi.
Si vocifera anche che ci fu tra loro un matematico "alternativo" che propose il sistema di numerazione a base 22, (considerando anche le orecchie), in quanto oltre da essere matematico, era un appassionato di proto-calcio (inteso come sport) praticato da tale popolazione, avendo calcolato con l'ausilio del sofisticato calendario dei tempi, che circa 1500 anni dopo quello sport primordiale si sarebbe evoluto con la partecipazione contemporanea sullo stesso spazio delimitato, di 22 elementi, 11 per gruppo contendente (leggasi squadra).
Immediatamente dopo la sua proposta, gli furono mozzate le due orecchie, e il progetto base 22 morì sul nascere.
Ma le sue previsioni si rivelarono corrette.
Come succede in tutte le galassie i testi originali di Aristot andarono in gran parte perduti. Tuttavia dalle trascrizioni e dagli appunti dei discepoli risulta che , secondo lui, c elevato c sarebbe = cf . La dimostrazione però non fu mai scritta per la solita faccenda dei margini troppo piccoli. (Ma quando cambieranno formato ai libri per consentire di scrivere per benino le dimostrazioni che vengono in mente all'improvviso? )
In ogni caso si trovano varie conferme su a elevato a = a. Pare che Aristot avesse anche ipotizzato l'esistenza di una cosa tipo: j x j = -a , mandando in grande confusione tutti gli studenti)
Di certo anche b elevato b = d è giusto. Penso che Aristot ti avrebbe assegnato un buon voto, tipo da e a f.
Del matematico calciofilo andino avevo sentito parlare perchè, aveva cercato di fare il furbo adottando il modulo 5 5 5. In pratica metteva subdolamente in campo 15 giocatori della sua squadra invece di 11. Però gli era andata male anche li e non ricordo cosa gli avessero mozzato quella volta.
Bene, come vedi dal time-stamp del commento, abbiamo fatto l'a ed è ora di andare a dormire, anche perchè domani mattina mi dovrò svegliare prima delle g.
E' vero, ha ragione Aristot riguardo c alla c = cf; chissà perché mi ero convinto di considerare il terzo simbolo elevato al secondo simbolo anziché alla se stesso terzo simbolo....
E' che ragionavo prendendo come riferimento un sistema di numerazione formato da 7 "diti", 2 molari e un incisivo, ma venivo distratto dalla rivolta dei canini che chiedevano a gran voce il loro diritto di essere considerati e non discriminati e dal pensiero del matematico andino che qualunque innovazione proponesse, gli veniva mozzata in maniera random una parte anatomica.
Aldilà dei (necessari) toni scherzosi per affrontare il desueto, il ricorrere poco frequentemente ad un sistema di numerazione con base differente da 10, il calcolo delle operazioni eseguite sul riferimento di quel sistema può essere meno fluido rispetto al base 10.
Chissà se tra i Krull esiste l'analogo e raro fenomeno dell'esadattilia umana: come farebbero a chiamarla, chessò, l'equivalente in base 7 di "octadattilia"?
Ti suggerisco di contare i diti di mani e piedi di Aristot nella foto inserita da Daniela dentro l'articolo.
Noterai tre cose:
1. Aristot ha ben due (B) braccia, cosa mostruosa per un Krull.
2. Le due mani del filosofo hanno complessivamente un dito in più di G.
3 .Il totale dei diti tra mani e piedi fa ben BB ossia una base che riconoscerai al volo, molto importante.
L'abbondanza digitale è una concausa dell'elevato QI di Aristot. Pare che fosse superiore a CDG.