(Q) Riflessioni sulla riflessione del gatto *
Il quiz precedente è stato immediatamente risolto da Maurizio che ha, sicuramente, un'ottima conoscenza della specie felina. Non dimentichiamoci del suo gatto che riuscì a farla in barba sia a Schroedinger che alle severe leggi quantistiche.
La risposta è perfettamente corretta per come è stato presentato il quiz. Ma era solo l'antipasto... Per renderlo un po' più faticoso anche per i gatti, avrei dovuto aggiungere qualcosa di molto importante. Dove ho scritto: Ognuno di questi animali vuole incontrarsi con quello che sta alla sua sinistra e si muove di conseguenza", si dovrebbe scrivere: "Ognuno degli animali si muove costantemente in direzione del gatto alla sua sinistra". A questo punto la faccenda si complica anche per i felini. Non gli è, infatti, più permesso di ottenere il massimo risultato con il minimo sforzo, com'è di loro abitudine, ma di percorrere una traiettoria molto particolare. Basterebbe un'equazione differenziale e/o l per o sviluppo in serie per ricavare che la traiettoria necessaria allo scopo è una spirale logaritmica.
Le cose hanno preso una brutta piega (anche se non impossibile per i più esperti), ma potrebbero anche prevedere una soluzione che abbisogna solo del calcolo di un limite, senza scomodare nessuna spirale, cosa che i gatti sanno notoriamente eseguire.
Ecco, quindi, il vero quiz da risolvere senza bisogno dell' equazione della spirale e della sua lunghezza.
QUIZ RIVISITATO
Abbiamo una stanza quadrata dove ad ogni vertice si trova un. Ognuno di loro vuole incontrarsi con quello che sta alla sua sinistra e si muove costantemente in direzione del gatto alla sua sinistra. Assumiamo che la loro velocità sia la stessa e costante.
(1) Dove si incontrano?
(2) Quanto è lungo il loro percorso se consideriamo il quadrato di lato unitario?
La soluzione che ho in mente è quella propostami dalla mia celebre micina "Tigrotta", ma potrebbero essercene anche delle altre... Forza Maurizio & co. !
P.S.: Fatevi aiutare dai vostri gatti...
7 commenti
La simmetria del problema porta a individuare il centro come punto di convergenza degli spostamenti di ciascun gatto.
Supponiamo che ciascun gatto tenda a muoversi in direzione del vertice alla sua sinistra di una quantità
. Nel tempo che impiega a spostarsi, già deve modificare la sua direzione perché il suo obiettivo si è mosso a sua volta verso la propria sinistra della stessa quantità. Il disegno illustra la situazione descritta.
il rapporto tra i lati ( Li+1 ) / (Li ) è la ragione (q) di una progressione geometrica che ricavo da queste osservazioni:
( Li+1 ) = (Li ) (sen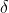
+ cos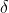 
) da cui ( Li+1 ) / (Li ) = 1/ (sen 
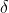+ cos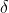 
)
Per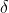
> 0 tale rapporto risulta < 1 quindi la somma della serie di tutti i valori di lunghezza dei lati dei quadrati (sempre più piccoli) dovrà valere: &space;=&space;1/(1-&space;1/(sen\delta&space;+cos\delta&space;))&space;=&space;(sen\delta&space;+&space;cos\delta)/(sen\delta&space;+cos\delta&space;-1))
moltiplicando questo valore per la lunghezza della stanza e per sen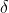
, assumendo per 
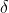un valore tendente a zero , ottengo la lunghezza del percorso totale seguito da ciascun gatto.
lunghezza percorso = Lato della stanza */(sen\delta&space;+cos\delta&space;-1)))
Applicando il teorema del marchese di De l'Hopital per i gatti troviamo che questo limite vale 1, quindi la lunghezza del percorso di ciascun felino coincide con la lunghezza del lato della stanza.
Queste elucubrazioni non sono mie ma di questo Red Tabbit
a cui ho sottoposto il problema. Non garantisco quindi che abbiano un senso perché, come certo sapete, i Red Tabbit sono dei burloni micidiali, sempre pronti a inventarsi storie assurde.
La soluzione di Mau fa uso di trigonometria (bestia nera dei gatti) e di una serie... La soluzione che ho in mente è diversa... POTETE ANCORA PROVARE A DARE LA VOSTRA SOLUZIONE!
Potrebbe essere illuminante la lettura dell'appendice in coda a questo articolo
Approssimo il movimento di ciascun gatto con una spezzata di segmenti di lunghezza proporzionale alla distanza dal gatto successivo. Se la distanza dal gatto successivo al movimento n-esimo è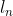
, il segmento della spezzata sarà di lunghezza 
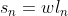. Con w che farò tendere a 0.
Quando il gatto sarà alla fine di questo segmento la sua distanza dal gatto successivo sarà:^2+w^2}=l_n\sqrt{1-2w+2w^2})
.
Applicando in sequenza questa relazione si ottiene che^n)
. Quindi ^n)
. L’espressione tra parentesi sviluppata in serie di Taylor limitatamente ai primi due termini è 
. Possiamo limitarci ai primi due termini poiché per w tendente a 0 l'approssimazione diventa esatta. La lunghezza totale della curva è la somma degli infiniti segmenti ^n})
. La parte che dipende da n è una serie geometrica. Sostituisco la sommatoria con il valore della somma della serie geometrica: }=wl_o\dfrac{1}{w}=l_0)
.
Quindi la lunghezza della spirale percorsa da ciascun gatto risulterebbe lunga quanto il lato del quadrato di partenza.
Aggiungo una figura che spero aiuti a seguire la mia risposta sopra.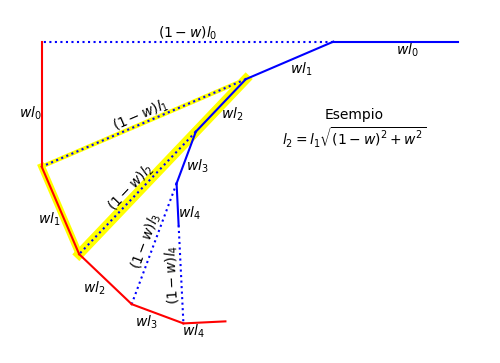
Questa mattina ho potuto parlare con gatti del vicinato. Dietro adeguato compenso in croccantini mi hanno concesso la loro consulenza.
Questa è il mio tentativo di traduzione nel linguaggio umano, nel linguaggio dei gatti bastano pochi miagolii e qualche movimento della coda.
Grande Fabrizio,
in certi casi è meglio affidarsi agli esperti (i gatti intendo...). La mia Tigrotta ha sviscerato una soluzione molto simile, condendola con un po' di matematica. Ma sai alle "signore" piace darsi un po' di importanza e complicare la vita al "compagno" (che sarei poi io...).