Questo articolo fa parte della serie "Disegnare in tre dimensioni: tra storia e pratica"

 

Tempo fa ci siamo divertiti a seguire la nascita della prospettiva, che ha cambiato drasticamente il modo di dipingere (e non solo) all'inizio del 1400. Non ripeto i vantaggi enormi che questa rivoluzione ha portato sia nelle manifestazioni artistiche sia nel cambiamento del ruolo dell'uomo nel contesto della Natura. Sicuramente ha permesso di rappresentare su un solo piano ciò che si vede realmente nelle tre dimensioni e ne è un esempio fantastico il disegno di Palazzo Vecchio di Firenze ottenuto da Brunelleschi.

Una conquista fantastica sotto svariati punti di vista,  che comporta, però, alcuni problemi pratici. Essa, infatti, simula perfettamente ciò che si vede, ma dice poco da un punto di vista "pratico", ossia "deforma" le dimensioni dell'oggetto che si disegna. Un rettangolo, ad esempio, viene trasformato in trapezio nella prospettiva centrale, mentre diventa un  quadrilatero qualsiasi in quella accidentale. L'occhio è pienamente soddisfatto, ma non la lettura delle vere dimensioni dell'oggetto.

Come sappiamo, per conservare le dimensioni e la forma, l'ideale è l'uso delle proiezioni ortogonali, ossia la rappresentazione dell'oggetto sui tre piani che lo caratterizzano: x,y; x,z; y,z. Esse ci danno la possibilità di leggere direttamente le vere dimensioni e i diversi angoli dell'oggetto, ma, ovviamente, non permette una visione d'insieme. In altre parole, le proiezioni ortogonali rappresentano le tre dimensioni in tre piani, ossia attraverso tre rappresentazioni bidimensionali. Ciò si vede  in Fig. 1 dove si sta utilizzando un parallelepipedo.

Sarebbe molto bello riuscire a trovare un compromesso, ossia avere una visione d'insieme il più vicina possibile a quella che l'occhio ci restituisce, mantenendo nel contempo la possibilità di misurare direttamente le vere dimensioni. Meno arte, forse, ma più facile utilizzo pratico.

Eccoci quindi all'assonometria il cui nome la dice lunga: misure in base agli assi. In altre parole, si vuole rappresentare una figura tridimensionale su un piano, sfruttando la direzione degli assi x, y e z. Ciò ci fa capire che vi sono infiniti modi per eseguire una rappresentazione di questo tipo, dato che gli assi possono essere scelti in qualsiasi modo si voglia. Alcune scelte non sarebbero molto utili, mentre altre sono ideali per un certo tipo di informazione, ad esempio di tipo militare. Noi ne abbiamo scelto tre che completano abbastanza bene la trattazione.

Poniamo l'asse z in verticale e tracciamo la sua perpendicolare (orizzontale), che rappresenterebbe il piano x,y. A questo punto ruotiamo questo piano attorno alla retta orizzontale di un certo angolo. Il piano x,y è adesso, visibile e possiamo permetterci di ruotare gli assi x e y su questo piano in modo da ottenere degli angoli particolari tra gli assi x e y e l'asse orizzontale. In Fig. 2 si sono riportate  tre possibilità che corrispondono a quelle che andremo a trattare tra poco.

Impostati gli assi della nostra proiezione, dobbiamo ricordarci che uno dei punti fondamentali che separa la visione prospettica da quella assonometria è la posizione  dei fuochi verso cui convergono le rette tra loro parallele. Nell'assonometria le linee parallele rimangono parallele e gli oggetti distanti non si riducono di dimensioni. In tal modo, essa riesce a rappresentare con2 temporaneamente tutte le dimensioni di un oggetto.  In poche parole, regala contemporaneamente tutte le informazioni delle proiezioni ortogonali, non rispettando, però, la visione reale di un oggetto. Il fatto che le rette parallele restino parallele vuole praticamente dire che i fuochi sono posti all'infinito.

Vediamone tre casi particolari (i più usati) utilizzando come solido da rappresentare un parallelepipedo.

Assonometria isometrica

Essa disegna i tre assi x, y e z a 120° l'uno dall'altro, come mostra la Fig.3.

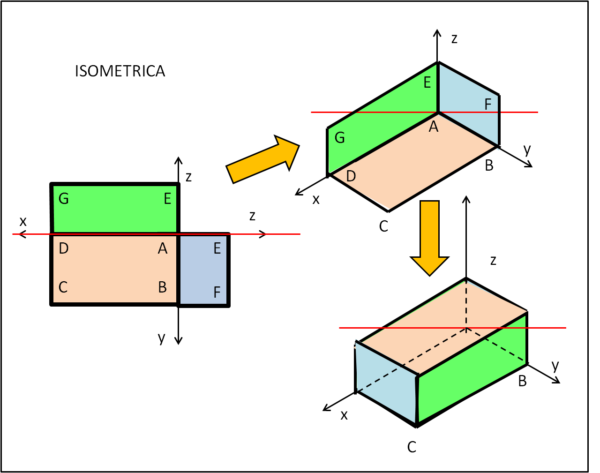
In altre parole, gli assi x e y formano uno stesso angolo (30°) rispetto alla retta orizzontale, perpendicolare all'asse z. Il disegno finale è decisamente semplice, ben più di quello ottenibile con la visione prospettica. Come già detto, le lunghezze dei lati del parallelepipedo sono mantenute e ciò che si deforma sono gli angoli tra gli assi x,y e z.  La costruzione si basa, quindi sul mantenimento delle lunghezze dei lati (ma non degli angoli tra di lor)o e sul mantenimento del loro parallelismo. La prima figura in alto a sinistra raffigura la parte "interna" del parallelepipedo, mentre quella in basso la superficie esterna. La costruzione è, ovviamente, la stessa e basta solo saper tracciare adeguatamente le linee tratteggiate che indicano i lati che non si vedono.

Questa assonometria si usa solitamente per cercare di avvicinarsi al massimo alla visione reale.

Assonometria monometrica

Incliniamo sempre gli assi x e y, ma manteniamo costante l'angolo di 90° che è sotteso dai loro lati (Fig. 4).

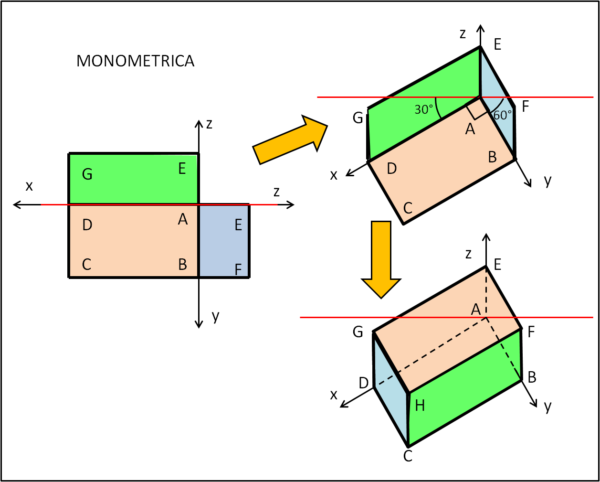
Ne segue che gli angoli degli assi x e y con la retta orizzontale rossa risultano 30 e 60° Gli assi hanno tutti gli angoli diversi tra di loro (x e z formano 120°, z e y 150°, y e x 90°).

La costruzione avviene con le stesse regole precedenti riguardo alle dimensioni e al mantenimento del parallelismo dei lati opposti delle varie facce del parallelepipedo.

Questa costruzione si usa principalmente per ottenere la migliore visione dall'alto, dato che si conserva proprio la faccia proiettata sul piano (x,y).

Assonometria cavaliera

In questo caso (Fig. 5) si mantengono  gli assi x e z, in modo tale da formare un angolo di 90°.

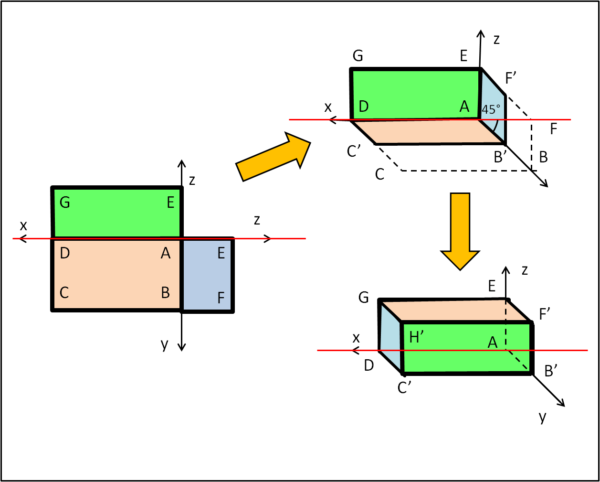
L'asse y, invece, è ruotato di 45° rispetto alla retta orizzontale rossa. Ne segue che l'angolo tra x e z risulta 90°, quello tra z e y, 135°, e ugualmente 135° tra l'asse y e l'asse x.

Questa costruzione viene usata per dare il massimo risalto alla visione frontale, ossia nel piano (x,z). Tuttavia, essa risulta -forse- la più deformante, per cui si usa spesso accorciare della metà tutti i lati perpendicolari obliqui.

Notiamo come sia facile passare da una visione assonometrica, ad esempio quella monometrica di Fig. 6, alle proiezioni ortogonali: bastano un paio di rotazioni e il gioco è fatto!

Breve storia dell'assonometria

Essa venne formalmente introdotta dal francese Gaspard Monge alla fine del Settecento. Nel corso dell'ottocento acquistò sempre maggior valore scientifico e venne trattata in modo sempre più articolato. L’assonometria è indubbiamente il metodo di rappresentazione più efficace per soddisfare le esigenze di precisione e immediatezza tridimensionale in un disegno tecnico. Tuttavia,  prima di assumere il ruolo di metodo ufficiale di rappresentazione, essa è stata usata per secoli, applicandola in modo empirico e intuitivo. La storia dell'arte è costellata di affreschi e mosaici in cui essa la fa da padrona ed è stata utilizzata anche da maestri come Cimabue e Giotto. Vediamone qualche esempio viaggiando attraverso i secoli.

Sicuramente era conosciuta dai greci come si nota nelle raffigurazioni pittoriche eseguite su coppe e anfore, sia in assonometria cavaliera che isometrica.

Furono i romani, però, a farne largo uso in modo quasi impeccabile sia nei loro affreschi che nei motivi decorativi.

Il sasso venne raccolto anche dai bizantini

e giunse fino a Cimabue e Giotto. Del primo vediamo la Maestà del Louvre, dove si manifesta chiaramente l'assonometria cavaliera, come indicato dalle varie linee riportate sul dipinto.

Giotto non è da meno, come si osserva nei troni dei patriarchi di Assisi, raffigurazioni  geometricamente perfette.

Tuttavia, Giotto cerca di fare un passo in avanti verso la prospettiva come si nota in due suoi affreschi. I punti di fuga sono ancora molto incerti, ma è chiara la differenza tra inclinazione del pavimento e della parte superiore degli edifici.

E poi arrivò Masaccio...