Questo articolo fa parte della serie "Disegnare in tre dimensioni: tra storia e pratica"

 

Continuiamo con il metodo descrittivo di Monge e proiettiamo una retta nel caso più generale e in alcuni casi particolari.

La retta

Il passaggio da segmento a retta è piuttosto semplice, anche se è necessario introdurre indicazioni diverse per i punti presenti nel grafico.

Consideriamo una retta r qualsiasi nel diedro di riferimento che sia comunque orientata. Essa deve intersecare PO e PV in due punti. che chiamiamo tracce della retta e che indichiamo con T1r (piano PO) e T2r (piano PV). Questi punti, per alcuni casi particolari possono anche essere "all'infinito", come vedremo tra poco. Come già fatto per il segmento, proiettiamo T2r sul piano PO: questo punto giace sulla Linea di Terra e lo indichiamo con T2'r. Il punto della LT che corrisponde alla proiezione di T1r su PV lo indichiamo  T"1r . Ciò viene fatto in modo del tutto analogo al segmento del capitolo precedente (Fig. 5). Infatti, T2r corrisponde al punto B = B" e T1r al punto A = A', così come le loro proiezioni: T'2r= B' e T"1r = A''. Le congiungenti T"1r con T2r e T1r con T '2r  rappresentano le due proiezioni della retta r e vengono chiamate r" e r'.  In pratica, abbiamo costruito il segmento di estremi T1r e T2r, il che non può sorprenderci dato che  per due punti passa una e una sola retta. Potremmo anche dire che le proiezioni della retta nei due piani PO e PV, ossia r' e r", sono individuate, dalle intersezioni con PO e PV di due piani α e β che contengono la retta r e che sono perpendicolari a PO e PV.

Riassumiamo quanto detto nella Fig.7

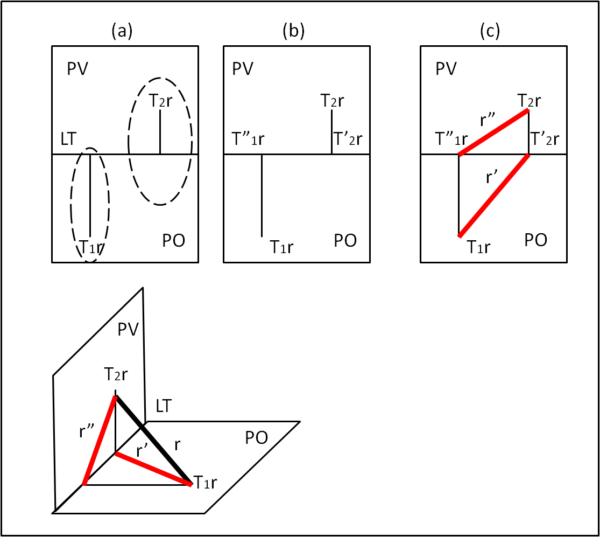
Iniziamo col disegnare le due tracce T1r e T2r (a). Individuiamo le proiezioni T"1r e T'2r sulla Linea di Terra (b). Congiungiamo  T"1r con T2r e T1r con T'2r (c) ottenendo le due proiezioni della retta r' e r". Per completezza nella parte inferiore della figura disegniamo la visione assonometrica di quanto appena eseguito.

Particolarmente interessanti sono le situazioni particolari della retta r.

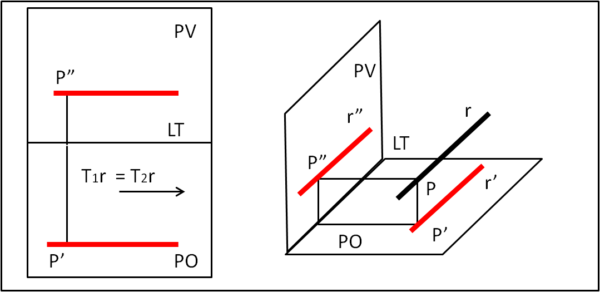
Retta parallela ai due piani PO e PV 

Essendo parallela ai due piani, essa deve essere parallela anche alla loro intersezione che, nel nostro caso, è  la LT. La retta, perciò, non ha tracce o, meglio, le sue tracce sono all'infinito. Di conseguenza lo sono anche le loro proiezioni sulla Linea di Terra.  In conclusione, le proiezioni r e r' della retta r non possono che essere due rette parallele alla Linea di Terra.  Esse, però, risultano ancora indeterminate. Se, imponiamo che la retta r passi per un punto P, le due proiezioni del punto sulla Linea di Terra individuano completamente le due proiezioni r' e r". Tutto ciò viene mostrato in Fig. 8, dove abbiamo inserito anche la visione assonometrica.

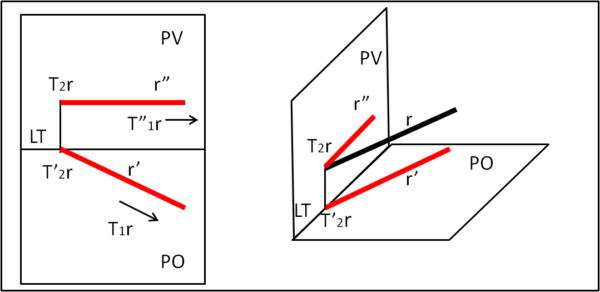
Retta incidente PV e parallela al piano PO

L'unica traccia della retta r è data dal punto T2r che ha T'2r come proiezione su PO . La seconda traccia (T1r) è all'infinito. Ne segue che r" deve passare per T2r ed essere parallela a LT. r', invece, deve passare per T'2r (= T2r) e andare all'infinito nella direzione di T1r (Fig. 9).

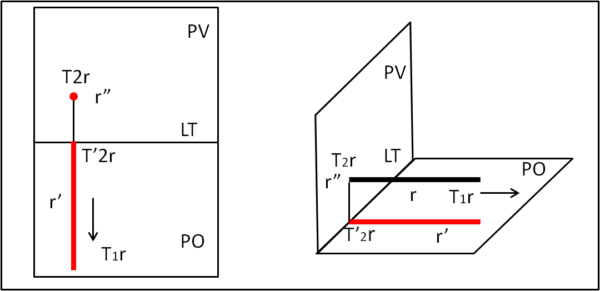
Retta perpendicolare al piano PV 

La traccia della reta sul piano PV è il punto T2r che ha T'2r come proiezione su PO. T1r è invece all'infinito. Ne segue che r' passa per T'2r e va all'infinito, mentre la r" si riduce al punto T2r (Fig. 10).

Retta passante per la LT

L'unica traccia conosciuta della retta è un punto su LT, per cui T1r= T"1r (o, analogamente, T2r = T2'r). Qualsiasi coppia di rette r' e r", passanti per questo punto, rappresentano  le proiezioni di una retta passante per LT. La nostra retta è quindi indeterminata. Per disegnarla è necessario definire un secondo punto su di essa, ad esempio P. Unendo T1r con P' abbiamo la proiezione r'; unendo T"1r con P" abbiamo r" (Fig. 11)

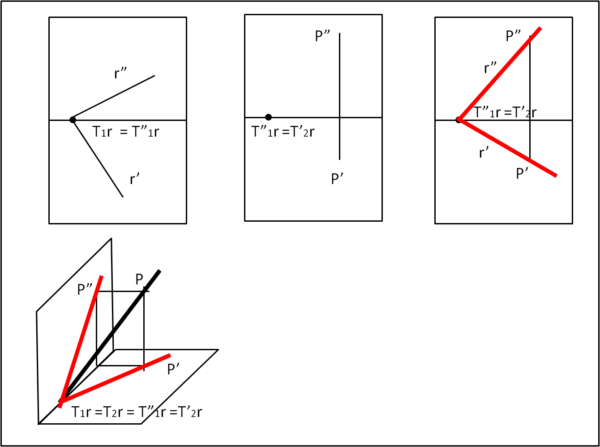
L'ultima costruzione ci dice anche le condizioni perché un punto P appartenga a una retta qualsiasi: le sue proiezioni P' e P" devono stare sulle proiezioni r'  e r" (Fig. 12)

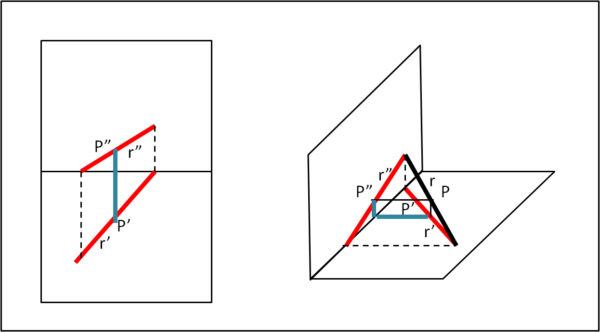
Notiamo che per seguire strettamente le regole abbiamo probabilmente complicato, a volte,  la descrizione della costruzione. Lo stesso risultato si poteva ottenere più facilmente proiettando direttamente la retta attraverso due piani passanti per essa e perpendicolari a PO e PV. Tuttavia, sarebbe stata necessaria una visione assonometrica, cosa che possiamo solo usare come verifica posteriore, ma non come base di partenza.

Per meglio capire cosa intendo dire poniamoci un semplice problema che deve essere risolto senza l'ausilio di visione assonometrica. Le regole descritte precedentemente rendono il tutto più rapido, mentre la visione assonometrica sarebbe più ostica da disegnare.

Problema:

Data una retta r, disegnare una retta s che intersechi la retta r in un punto P.

Utilizziamo la Fig. 13.

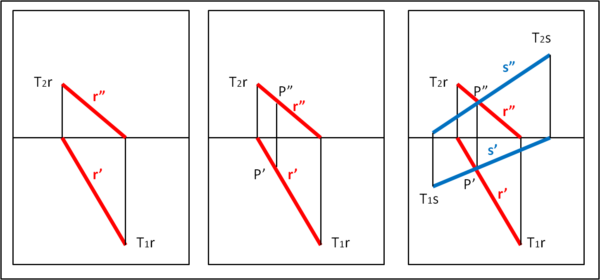
In (a) disegniamo la retta r con i le sue tracce T1r e T2r. Scegliamo un punto P su di essa. Affinché il punto stia su di essa le sue proiezioni P' e P" devono stare sulle proiezioni r' e r" rispettivamente (b). Per disegnare una retta incidente la retta r nel punto P, basta tracciare le proiezioni s' e s" di una retta s che passino per P' e P". Ovviamente, ve ne sono infinite e in (c) ne abbiamo scelta una a caso. In conclusione: due rette sono incidenti se esiste un punto P le cui proiezioni P' e P" stiano sia sulle proiezioni r' e r" che su s' e s".

Disegniamo, invece, la Fig. 14.

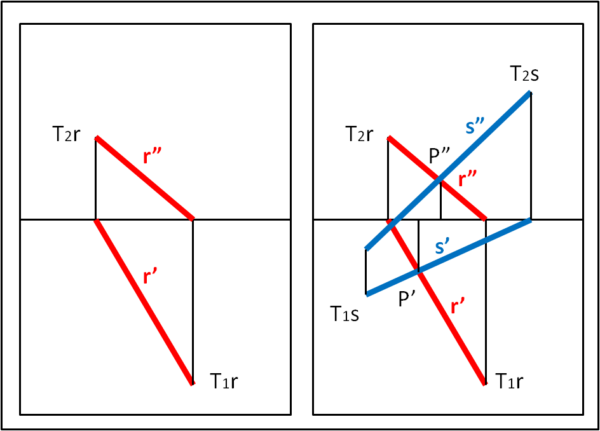
Le due rette non hanno in comune nessun punto, infatti l'intersezione tra r' e s' non corrisponde all'intersezione tra r" e s". In poche parole, le due rette sono sghembe.

continua...