La matematica, e la geometria in particolare, possono portare a soluzioni di problemi in cui si ammira una vera eleganza. Spesso, molte sono le vie per arrivare alla conclusione, ma quando si aggiunge semplicità e rapidità si compie una piccola opera d'arte. A volte si usa la "forza bruta" che, però, gratifica molto meno di una procedura che è bella ed elegante di per sé.

Approfitto della domanda di Cesco e Alberto (relativa a questo articolo per dare una risposta abbastanza soddisfacente (riporto la prima che mi è venuta in mente e mi accontento) per poi mostrare una soluzione di pura eleganza a un problema che sembrerebbe risolversi "normalmente" in modo più elaborato.

Cominciamo con la risposta a Cesco e Alberto che hanno chiesto di dimostrare che il segmento rosso AD è uguale a RB e che i due segmenti sono paralleli.

Riprendiamo la figura...

Il "trucco" per risolvere il problema è quello di ruotare il triangolo CAR di 90° verso destra in modo da ottenere la figura che segue:

Basta tracciare la perpendicolare da D a CR e il gioco è fatto. Notiamo che la rotazione non ha minimamente cambiato posizione e dimensioni dei due segmenti originali CD = AD e RB=AB

Esiste  l'uguaglianza di molti segmenti:

AQ = CQ = QN = MP = PB = PD

Consideriamo il quadrilatero MQNP. Lui è un rettangolo in quanto ha i quattro angoli uguali a 90° per costruzione, per cui:

MQ = PN

Consideriamo i due triangoli rettangoli colorati in verde della figura che segue

AN = 2 QN

MD = 2 MP = 2 QN

AN = MD

NB = PB - PN

CM = CQ - MQ = PB - QN

NB = CM

I due triangoli verdi sono uguali e, quindi, ne segue che:

AB = CD

ossia

AD = RB

c.v.d.

Vediamo ora un caso in cui l'eleganza si fa sentire veramente...

Disegniamo un quadrato di lato s e, a fianco, inseriamo un quadrato più grande di lato sconosciuto. Vogliamo sapere quanto vale l'area del triangolo giallo (vedi Fig. 1).

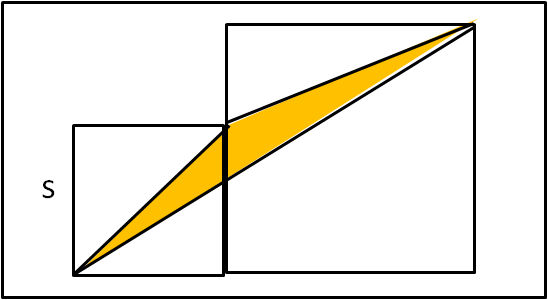
La  cosa che sembrerebbe più ovvia è chiamare x il lato del secondo quadrato e suddividere la figura in vari triangoli, come mostra la Fig. 2

Facendo un minimo di conti è facile calcolare le aree dei vari triangoli:

Area triangolo azzurro = (x - s)x/2

Area triangolo rosa = (s + x)x/2

Area triangolo verde = s²/2

Sappiamo anche l'area dell'intera figura composta dai due quadrati:

Area totale = s² + x²

Per ottenere l'area del triangolo giallo basta togliere all'area totale quella dei tre triangoli:

Area triangolo giallo = s² + x² - s²/2 - (x - s)x/2 - (s + x)x/2

Una semplice espressione che si può semplificare...

Area triangolo giallo = s² + x² - s²/2 - (x² - sx)/2 - (sx + x²)/2 = (2s² + 2x² - s² - x² + sx - sx - x²)/2

Area triangolo giallo = s²/2

Tutto perfetto? Sì, sì... ma il fatto che il risultato non dipenda assolutamente da x (ossia dalle dimensioni del secondo quadrato) ci dice chiaramente che il metodo usato si è basato sulla "forza bruta" e non sull'eleganza. Eppure, bastava pensarci un attimo e ricordare che l'area di un triangolo è dato dal prodotto di base per altezza diviso due.

La Fig. 3 ci mostra una soluzione più semplice, breve e, sicuramente, più elegante...

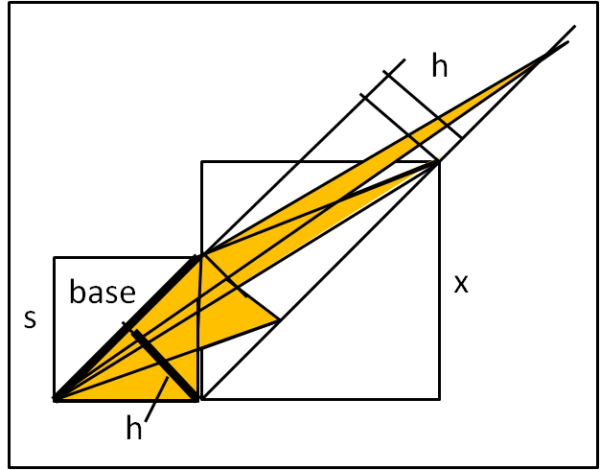
Tracciamo le diagonali dei due quadrati. Esse sono, ovviamente, parallele, e la distanza tra di loro è quindi costante. Il triangolo giallo ha come base la diagonale del primo quadrato e come altezza proprio h. Ma la stessa area è quella degli altri triangoli gialli che condividono la stessa base (diagonale del quadrato piccolo) e la stessa altezza, che è la distanza costante tra il prolungamento delle due diagonali.

E' ovvio, perciò, che il risultato sia sempre lo stesso, indipendentemente dalla posizione del vertice più a destra.  L'area di tutti i triangoli è sempre e comunque uguale alla metà di quella del quadrato di lato s, ossia s²/2.

Beh... questa sì che è eleganza. Accostarsi a queste piccole opere d'arte non può che fare amare la geometria!