Bravissimo, come sempre, il nostro Andy, che, pur rinunciando al teorema delle secanti, è riuscito,  manipolando sapientemente gli angoli, a giungere alla soluzione, utilizzando la trigonometria.

In realtà, il problema è più semplice di quanto possa sembrare e si può risolvere senza la trigonometria. A parte l'applicazione del teorema delle secanti, la proprietà fondamentale di un triangolo qualsiasi che domina la soluzione è veramente elementare e possiamo definirla come segue:

Dato un triangolo qualsiasi tracciamo da un punto P qualsiasi di un suo lato la congiungente con il vertice opposto. Il rapporto tra le aree dei due triangoli così ottenuti  è uguale al rapporto tra le parti in cui è stato diviso il lato di partenza dal punto P. Per dimostrala basta rico9rdare la formula che regala l'area di un triangolo, ossia base per altezza diviso due.

Il vero problema è, perciò, la scelta dei triangoli più convenienti per arrivare alla soluzione e, in particolare, la determinazione dell'area totale del triangolo di partenza.

Descriviamo  questa soluzione con tutti i passaggi, anche i più semplici, per  meglio chiarire eventuali confusioni o incertezze, iniziando col riproporre la figura dell'esercizio

 

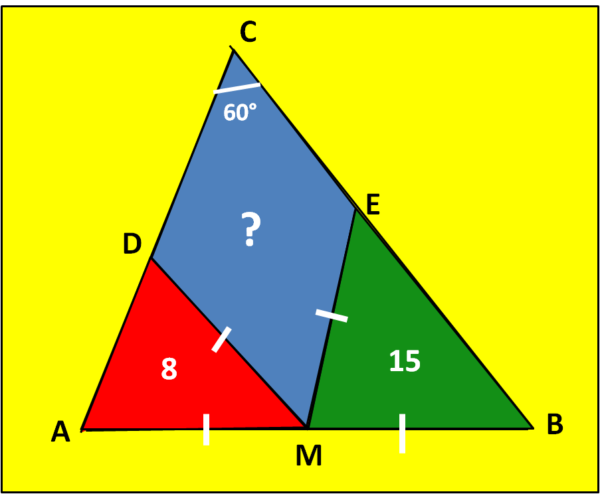
Iniziamo tracciando la circonferenza di centro M e raggio AM in Fig. 1.

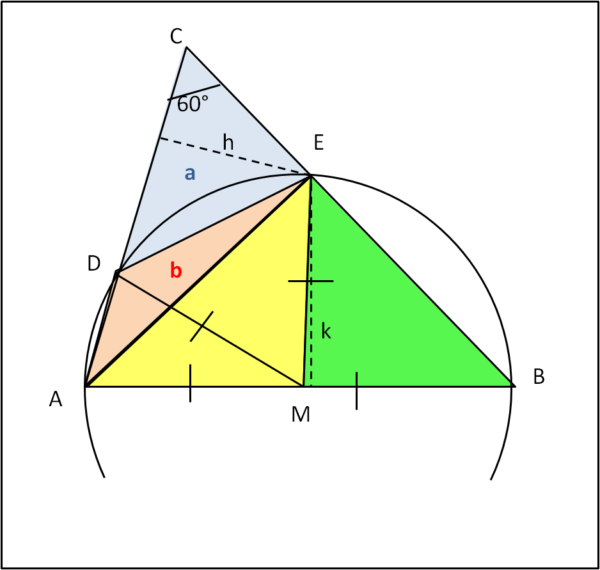
Essa, a seguito delle ipotesi di partenza, deve passare anche per i punti D, E e B. Coloriamo in azzurro il triangolo CED (dopo aver tracciato la corda ED) e indichiamo la sua area come a. Dal punto C sono tracciate due secanti al cerchio (CA e CB). Applichiamo il teorema delle secanti:

CA/CB = CE/DC                           .... (1)

Ne segue che il triangolo iniziale ABC è simile al triangolo CDE.  Essi infatti hanno un angolo in comune (quello in C = 60°) e i lati in proporzione (come dice la (1)).

Non basta però... Tracciamo il segmento AE. L'angolo AEB deve essere retto (angolo alla circonferenza sotteso da un diametro), da cui segue che anche CEA è un angolo retto. Il triangolo CEA è rettangolo con un angolo di 60°. Ne segue che:

AC = 2 CE

La (1) ci dice, allora, che il rapporto tra CA e CE è uguale a 2. Essendo i triangoli ABC e CDE simili, le loro area stanno nel rapporto 4.

S(ABC) = 4 a                          .... (2)

Calcoliamo l'area del triangolo CDE, che chiamiamo b.

b = DA h/2

Mentre l'area a vale:

a = CD h/2

da cui:

b/DA = a/CD

a/b = CD/DA                      .... (3)

Consideriamo, adesso, i triangoli verde e giallo. Essi hanno la stessa base (il raggio AM = MB) e la stessa altezza k (attenzione! EM NON è obbligato a coincidere con k), per cui hanno anche la stessa area. Possiamo quindi concludere che il triangolo AEB ha un'area doppia di MEB.

S(AEB) = 2S(MEB).

Ma S(MEB) è un dato del problema e vale 15

S(AEB) = 30                     .... (4)

L'area di ABC è data dalla somma dei triangoli di area a, b e  30, ma è anche uguale a 4a (vedi la (2)):

4a = a + b + 30

b = 3a - 30                         .... (5)

Consideriamo i triangoli grigio e viola di Fig. 2

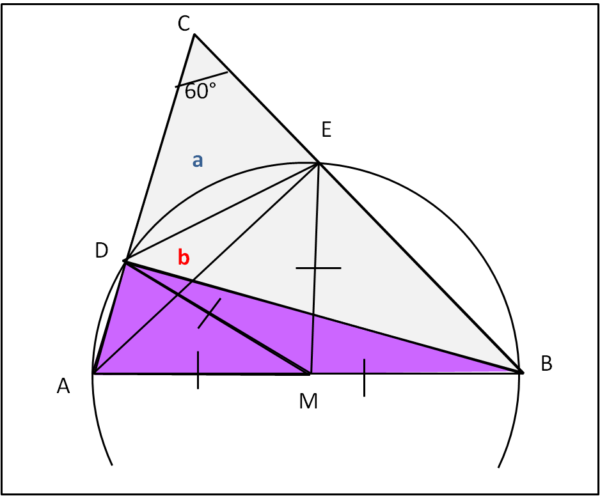
S(CDB) = 1/2 CD · DB              ....(6)

S(DAB) = 1/2 DA · DB                .... (7)

DB è altezza per entrambi i triangoli dato che l'angolo alla circonferenza ADB deve essere retto. Indichiamo l'area di DEB come c (Fig. 3)

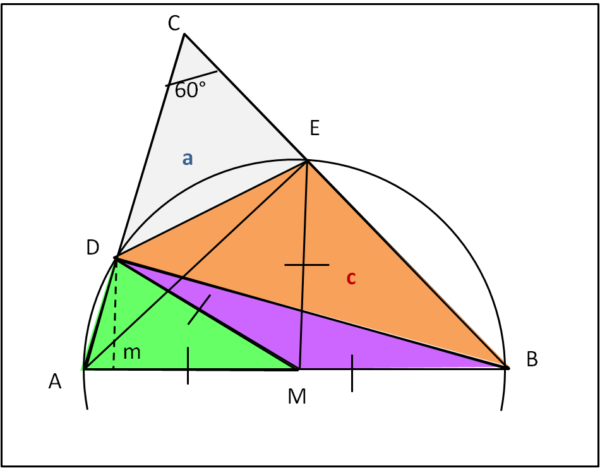
Sappiamo anche che:

S(DAM) = S(DMB)

dato che hanno come base la stessa base (il raggia MA) e la stessa altezza m

Ma noi conosciamo l'area di DAM ed essa vale 8. Ne segue che l'area di DAB è uguale a 16. Le (6) e (7) diventano

S/(CDB) = 1/2 CD · DB  = a + c

S(DAB) = 1/2 DA · DB = 16

da cui:

CD/DA = (a + c)/16                  .... (8)

Ma la (3) ci dice quanto vale questo rapporto:

CD/DA = a/b

per cui:

a/b = (a + c)/16                  ....(9)

L'area del triangolo ABC vale 4a (vedi (2)), e può anche essere scritta come somma di tre aree:

S(ABC) = a + c + 16 = 4a

da cui la relazione tra a e c:

c = 3a - 16                                    .... (10)

Bene, abbiamo nelle nostre mani tre relazioni tra a, b e c ((5), (9) e (10)). Riscriviamole:

b = 3a - 30     

a/b = (a + c)/16 

c = 3a - 16     

Portiamo c  e b nella seconda equazione:

a/(3a - 30) = (a + 3a - 16)/16

(4a – 16)/16 = a/(3a - 30)

16 a =(4a - 16)(3a - 30)

16a = 12a² - 120a - 48a + 480

raggruppando  e dividendo per 4

4a = - 3a² - 42a +120

3a² – 46a + 120 = 0

Le due soluzioni sono:

a = (23 +/-√(529 - 360))/3

a = (23 +/- 13)/3

a1 = 10/3 = 10

a2 = 12

La prima soluzione è da scartare in quanto porterebbe a un valore dell'area ABC pari a 4a, ossia a 40/3. Ma 40/3 è uguale a 13.333... che è minore di 15 che è l'area del solo triangolo EOB.

La soluzione da accettare è quindi la seconda che porta ai seguenti valori:

S(ABC) = 48

Per avere l'area del quadrilatero DCEM basta togliere all'area totale le aree dei due triangoli noti fin dall'inizio:

S(DCEM) = 48 - 15 - 8

S(DCEM) = 25

Notiamo che tutto il problema si risolve calcolando l'area del triangolo di partenza...