Sappiamo tutti cosa siano le funzioni seno e coseno. da un punto di vista trigonometrico. Sappiamo anche che queste due funzioni possono essere approssimate molto bene attraverso dei polinomi, applicando gli sviluppi in serie di Taylor e Mc Laurin (potete trovare  approfondimenti ed esercizi QUI e nei capitoli precedenti del Corso di Matematica). L'approssimazione si svolge analiticamente con passi successivi, aggiungendo, di volta in volta, una nuova funzione data da potenze sempre più alte di x, divise pe un numero fattoriale crescente. Scriviamo i primi termini del seno e del coseno

sin x = x - x³/3! + x⁵/5! - x⁷/7! + ....

cos x = 1 - x²/2! + x⁴/4!- x⁶/6! + ...

Vediamo, come esempio, la costruzione di sin x in Fig. 1

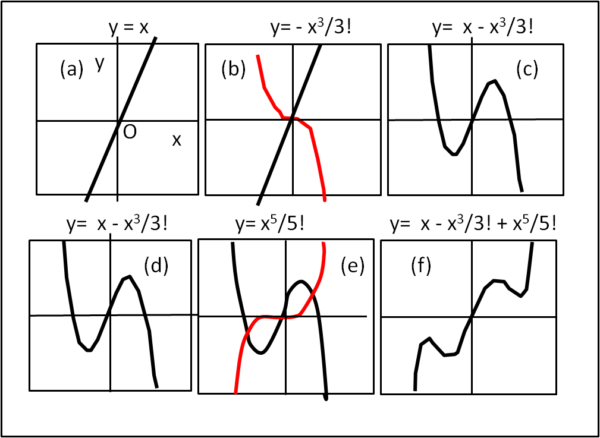
In (a) introduciamo il primo termine, ossia y = x (la retta a 45° rispetto agli assi). In (b) aggiungiamo il secondo termine, ossia la funzione (rossa) y =- x³/3!. Sommiamo le due funzioni e otteniamo la curva nera (c). A questa (d) aggiungiamo il terzo termine, ossia la funzione rossa y = x⁵/5! (e), che, sommata a quella precedente, ci porta alla curva (f). Si vede bene come ogni termine aggiuntivo migliori l'approssimazione di sin x nell'intorno del punto O.

In Fig.2 mostriamo l'approssimazione raggiunta con il nono e il ventisettesimo grado. Ormai il seno è praticamente esatto per valori sempre più grandi dell'intervallo attorno all'origine degli assi. Notiamo anche come tutte le funzioni aggiuntive siano dispari.

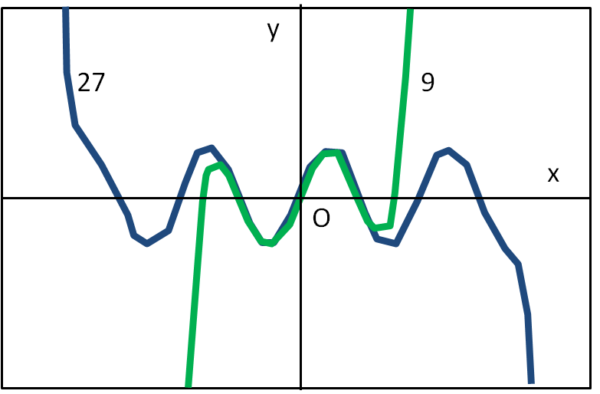
Dopo questo breve riassunto, vediamo di calcolare il seno di x, ricavando la sua espansione in serie per via puramente geometrica.

Disegniamo un cerchio di raggio unitario e un certo angolo s al centro. Lo stesso valore di s, in radianti, lo ha anche l'arco di circonferenza sotteso da questo angolo. Definiamo come seno di x l'ordinata del punto A.

Prima di procedere, introduciamo una simpatica curva che assomiglia molto alla spirale di Archimede, ma che, in realtà, non lo è. La chiamiamo involuta del cerchio e la possiamo definire in modo molto pratico nella Fig. 3.

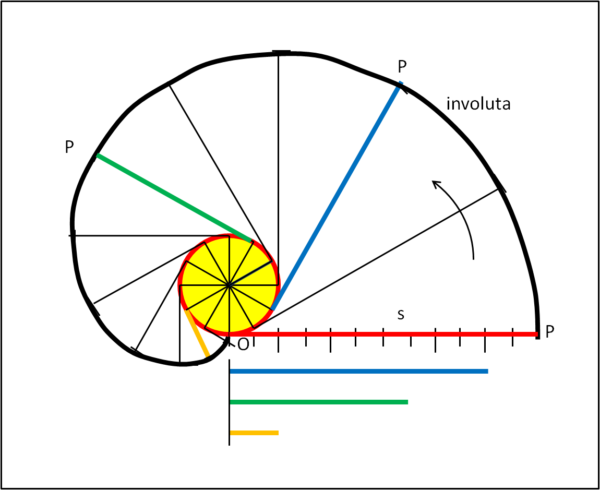
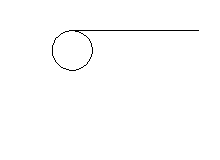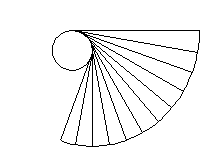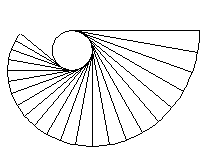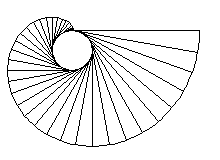
Abbiamo un cerchio giallo e una corda rossa ben tesa che è fissata al cerchio nel punto O. Iniziamo ad avvolgere la corda attorno al cerchio e, se la lunghezza è proprio uguale alla circonferenza, la corda finisce esattamente in O. Come costruire l'involuta? Semplice... dividiamo il cerchio in 12 parti uguali (ad esempio) e facciamo lo stesso per la corda s (OP). In ogni punto di intersezione dei 12 raggi con la circonferenza tracciamo la tangente al cerchio. A partire dal punto di tangenza si segna su di essa un segmento uguale a quello della corda meno la parte già utilizzata. In particolare, la linea blu è uguale a 10 parti della corda (12 - 2). Quella verde è uguale alla corda meno 5 parti (12 - 5 = 7). Quella arancione è lunga solo 2 parti della corda (12 - 10 = 2). La curva nera è proprio l'involuta che, al termine, della costruzione avvolgerà perfettamente e completamente il cerchio.

Notiamo bene che la stessa curva si ottiene sia avvolgendo la corda sia svolgendola. In altre parole se la corda avvolge completamente ed esattamente il cerchio, possiamo srotolarla seguendo lo stesso percorso e ottenere la corda in posizione orizzontale (OP).

Per meglio comprendere l'intera faccenda possiamo vedere l'animazione della Fig. 4.

Imparata questa semplice costruzione, torniamo al nostro cerchio di partenza e cerchiamo di calcolare geometricamente l'ordinata del punto S (Fig. 5)

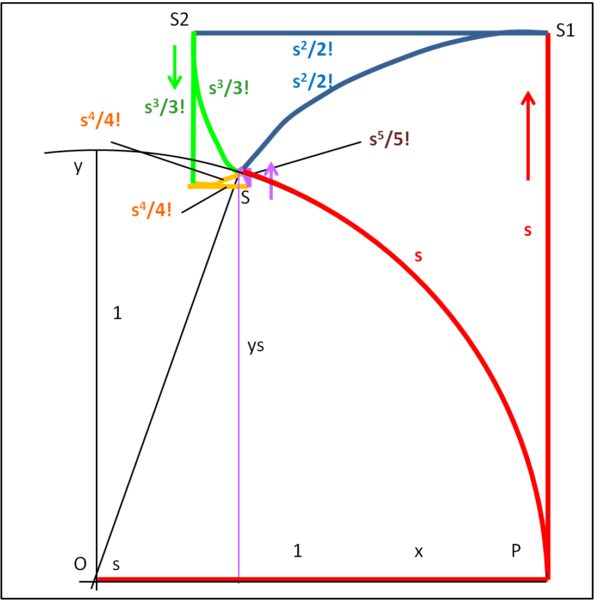
Possiamo immaginare che vi sia una corda, di lunghezza s, che avvolga un arco  della circonferenza (PS) . Non ci resta che srotolarla mantenendo fisso il punto P. La corda descrive la curva azzurra che va da S a S1. La corda rossa è ora perpendicolare all'asse delle x e la sua lunghezza è proprio s.

Tuttavia, la cosa più importante è la lunghezza della curva azzurra, ossia dell'involuta dell'arco di cerchio s. Si può dimostrare (non lo faremo, per ora, dato che è cosa non certo facile) che essa vale s²/2. Dobbiamo ricordare che ogni curva possiede la sua involuta, non solo il cerchio. Ebbene, qual é l'involuta della curva azzurra di lunghezza s²/2 ?

Graficamente basta "srotolare" la curva azzurra e portarla a diventare un segmento orizzontale (S1S2). Per come abbiamo eseguito l'operazione, abbiamo che S1S2 = s²/2. L'involuta è la curva verde che ha una lunghezza pari a s³/6 = s³/3!

Ormai il gioco lo conosciamo e non resta che tracciare l'involuta della curva verde. Il segmento verticale verde ha come lunghezza s³/3!, mentre la nuova involuta arancione ha lunghezza s⁴/4!. Tale è anche la lunghezza del segmento arancione orizzontale. La sua involuta è la curva viola che ha come lunghezza s⁵/5! e così pure il segmento corrispondente verticale viola. Non abbiamo più spazio, ma ormai l'andamento della procedura è chiaro: basta tracciare le involute delle involute e tenere conto della loro lunghezza.

Notiamo subito che l'ordinata del punto S, ossia il nostro seno dell'angolo s, è dato dalla somma (con segno) di tutti i segmenti verticali ottenuti con la costruzione precedente, In altre parole possiamo scrivere:

y_S = s - s³/3! + s⁵/5! - s^7/7! + ....                 .... (1)

Ovviamente, compaiono solo i termini con esponenti dispari in quanto gli altri sono orizzontali.

Come indicato all'inizio, chiamiamo sin x proprio l'ordinata del punto s e quindi la (1) è una sua approssimazione che migliora aumentando i termini. Non ci dobbiamo stupire che il risultato sia proprio quello dimostrato da Taylor attraverso le derivate successive. Il polinomio finale non è altri che la somma di segmenti sempre più piccoli...

Immediata è anche la definizione del coseno, ossia dell'ascissa del punto S. In questo caso dobbiamo prendere solo i segmenti orizzontali e si ottiene:

x_S = 1 - s²/2! + s⁴/4! - s⁶/6! + ....

Ho sicuramente scontentato qualcuno, dato che sarebbe veramente importante CALCOLARE  le lunghezze delle varie involute, ma è lavoro troppo faticoso da fare durante l'estate, che, finalmente, si è ricordata di esistere, ma che, malgrado ciò che ci propinano i falsi esperti televisivi, è anche durata molto poco (almeno in Piemonte...). Al prossimo inverno che sarà sicuramente il più caldo degli ultimi milioni di anni!