Questo articolo voleva originariamente essere un quiz. Tuttavia, vista la poca voglia di mettersi alla prova da parte di quasi tutti i lettori, preferisco descrivere il problema punto per punto. Chi volesse arrivare da solo alla soluzione può sempre interrompere la lettura e tentare di proseguire da solo.

Un ricco possidente terriero, dal carattere un po' peculiare, lascia ai suoi due figli un appezzamento di terreno esagonale, molto grande e ricco. Tuttavia, pone un vincolo ben chiaro: i due figli verranno in possesso del terreno solo se saranno capaci di dividerlo in due parti che abbiano esattamente la stessa area, senza fare nessun calcolo, ma solo attraverso un aratro che delimiti le parti di uno e dell'altro.

La figura che segue mostra il terreno dalla forma di un esagono irregolare che ha il vantaggio di possedere un cerchio inscritto, il cui centro O è ben segnalato.

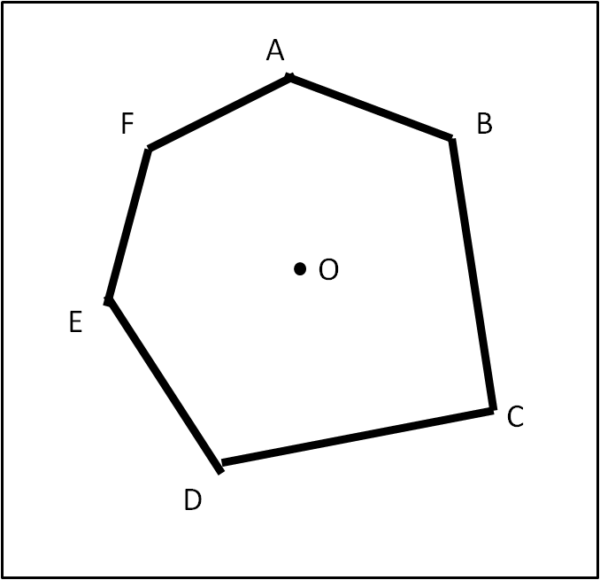
I due figli sono molto "svegli" e nel giro di un tempo brevissimo riescono a soddisfare il padre e ad entrare, ciascuno, in possesso di metà del terreno. Come hanno fatto?

Chi vuole procedere da solo può interrompere qui la lettura.

I due fratelli ricordano molto bene il teorema di Pitot, ingegnere francese del 1700, il quale ha dimostrato che le somme  dei lati alternati di un poligono circoscritto a un cerchio sono uguali. Mi spiego meglio... In un quadrilatero la somma dei lati opposti è uguale; in un esagono, la somma del primo, del terzo e del quinto è uguale alla somma del secondo, del quarto e del sesto; in un ottagono, la somma del primo, del terzo, del quinto e del settimo è uguale alla somma del secondo, del quarto, del sesto e dell'ottavo; e via dicendo.

La dimostrazione è molto semplice e possiamo mostrarla per un esagono in Fig. 2.

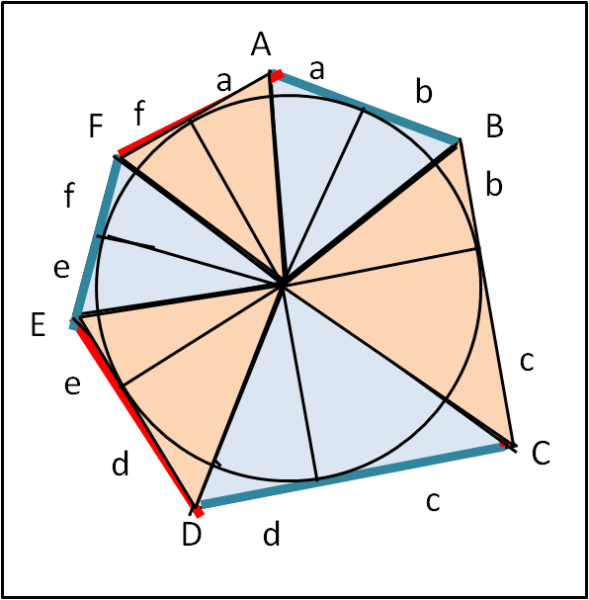
Da ogni vertice sono tracciate le due tangenti al cerchio. Dobbiamo dimostrare che AF + BC + ED  è uguale ad AB + DC + EF. Sappiamo, però, che le due tangenti tracciate da un punto esterno alla circonferenza formano segmenti uguali, per cui:

AF + BC + ED = f + a + b + c + d + e

AB + DC + EF = a + b + c + d + e + f

da cui la tesi.

Consideriamo, adesso, i triangoli rosa e azzurri.

Essi hanno per base i lati dell'esagono e per altezza il raggio r del cerchio. I tre triangoli rosa hanno, perciò, la somma delle aree uguale a:

(AF + BC + ED)r/2

Mentre quelli azzurri hanno la somma delle aree uguale a

(AB + DC + EF)r/2

Per quanto dimostrato precedentemente le due somme sono uguali. Al primo fratello vanno le aree rosa e al secondo le aree azzurre.

La divisione a metà del terreno è stata eseguita perfettamente tracciando con l'aratro le congiungenti il centro del cerchio con i vertici dell'esagono.