Questo articolo fa parte della serie Relativisti

 

        Relativisti 3: RIEMANN                                                                                                      8 gennaio 2021

 

Rompendo il legame con lo spazio sensibile e rendendo astratto il ragionamento, diventa possibile infrangere tabù millenari per approdare a visioni controintuitive che la nostra esperienza quotidiana tende istintivamente a rifiutare.
Quando poi si riconducono le conclusioni teoriche al mondo concreto, emergono risultati sorprendenti che collegano la fisica alla geometria, idee che ritroveremo mezzo secolo più tardi nella formulazione della relatività generale di Einstein: la forza subita dai corpi è il prodotto della geometria, in altri termini, la forza può essere interpretata come dovuta alla curvatura dello spazio.

 

Riemann e la geometria ellittica

Gli starnazzamenti dei beoti, paventati da Gauss, a seguito della pubblicazione della genesi di nuova geometria , alternativa a quella euclidea, da parte di Bolyai e Lobacevskij, non si fecero attendere.

Ma vi fu anche chi prese con grande serietà questa rottura della tradizione e si inoltrò ulteriormente in quel nuovo territorio sconosciuto.

Indubbiamente il fatto che il quinto postulato, della unicità della parallela a una retta data, passante per un punto, fosse stato soppiantato con l’eretica ipotesi di infinite parallele possibili, era solo una delle due possibilità. L’altra era che per il punto assegnato non passasse proprio alcuna parallela.

Questa scelta dava origine ad una ulteriore geometria, ben nota ai naviganti fin dal tempo dei greci: quella della sfera. Astronomi, cartografi, marinai, persino la bibbia, concordano sul fatto che la terra è un globo, con buona pace dei terrapiattisti di ieri, di oggi e di domani.

Ma vediamo più da vicino cosa successe e quali furono i protagonisti.

Proprio nell’anno in cui Lobacevskij tenne all’università di Kazan la dissertazione in cui illustrava i “Princìpi della geometria” (pubblicati solo tre anni più tardi), nasceva a quasi tremila chilometri di distanza, nella bassa Sassonia, Bernhard Riemann, secondo dei sei figli di un pastore protestante.

La sua inclinazione per la matematica viene notata e incoraggiata dal suo insegnante e, a soli 10 anni, è già padrone di concetti avanzati di matematica e geometria. Negli anni del liceo, con il supporto del preside Schmalfuss, un matematico professionista, sviluppa un particolare interesse per la teoria dei numeri, che lo accompagnerà per il resto della sua breve vita, conclusa a soli 39 anni. All’università di Gottinga si iscrive inizialmente a Teologia, una scelta dettata dal desiderio di contribuire al sostegno della famiglia diventando predicatore. Ma il padre, resosi conto di quali siano le grandi potenzialità di Bernhard, lo incoraggia a dedicarsi allo studio della matematica. L’influenza di Gauss, a Gottinga, e di altri grandi matematici, a Berlino, gli consentono di sviluppare rapidamente tutto il suo potenziale. La sua prima tesi di dottorato, sulle funzioni di variabili complesse, del 1851, suscita l’entusiasmo di Gauss che, normalmente poco incline agli elogi, si esprime in questi termini:

“La dissertazione presentata da Herr Riemann offre prove convincenti che ha svolto indagini attente e penetranti in quelle parti dell’argomento trattate, che ha una mente creativa veramente matematica, e che possiede una feconda originalità. La presentazione è notevole, concisa e per certi versi bellissima.”

Nel 1854, a 28 anni, presenta la sua seconda tesi, con la quale si qualifica come professore universitario a Gottinga, dove erediterà in seguito la prestigiosa cattedra di Gauss. La sua lezione inaugurale getta le basi per lo studio delle geometrie non euclidee, il germe della Relatività.

Nel suo saggio “Sulle ipotesi che servono come fondamento della geometria” incontriamo, tra gli altri concetti, quello della distanza in un spazio di N dimensioni, in cui generalizza un metodo precedentemente sviluppato da Gauss, e la nozione di curvatura nello spazio a N dimensioni. L’originalità della visione di Riemann sta nella sua globalità: la geometria è intesa come studio di “varietà” di un numero qualsiasi di dimensioni, in qualsiasi tipo di spazio. Più che trattare di punti, rette, piani, o di spazio nel senso ordinario, si parla di insiemi di ennuple ordinate che vengono raggruppate secondo certe regole.

Rompendo il legame con lo spazio sensibile e rendendo astratto il ragionamento, diventa possibile infrangere tabù millenari per approdare a visioni controintuitive che la nostra esperienza quotidiana tende istintivamente a rifiutare.

Quando poi si riconducono le conclusioni teoriche al mondo concreto, emergono risultati sorprendenti che collegano la fisica alla geometria, idee che ritroveremo mezzo secolo più tardi nella formulazione della relatività generale di Einstein: la forza subita dai corpi è il prodotto della geometria, in altri termini, la forza può essere interpretata come dovuta alla curvatura dello spazio.

Ma torniamo alla genesi di quella particolare geometria non euclidea in cui il quinto postulato viene negato dalla affermazione “dato un punto non esiste alcuna parallela ad una retta data, passante per quel punto”.

La principale implicazione di questo assunto è che mette in crisi anche un altro postulato euclideo, precisamente il secondo, che assicura che “ogni segmento si può estendere indefinitamente”.

Fu proprio Riemann a cogliere questo fatto fondamentale e a far notare nella sua dissertazione del 1854 che il secondo postulato di Euclide si poteva interpretare in due diversi modi:

Ogni retta è infinita

Ogni retta è illimitata

Bolyai, Lobacevskij e lo stesso Gauss si erano limitati a considerare solo due possibili geometrie, e non tre, perché avevano interpretato il secondo postulato nella prima maniera.

Ma mentre la prima formulazione rende impossibile la “terza via” alla geometria, la seconda ne permette una realizzazione, analoga a quella sferica, in cui le rette sono illimitate, ma non infinite.

Il concetto di illimitato corrisponde all’estensione ed è qualitativo, mentre il concetto di infinito è relativo alla misura ed è quantitativo.

Il contesto di riferimento per questa geometria è espresso dal seguente modello.

Il “piano” è costituito da una superficie sferica

Il “punto” è una qualsiasi coppia di punti diametralmente opposti, appartenenti al “piano”

La “retta” è una qualsiasi circonferenza massima del “piano”

Visualizziamo queste entità nella seguente figura.

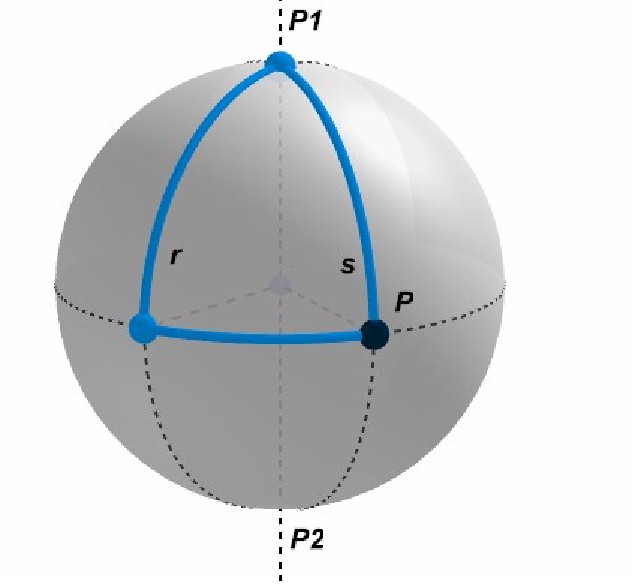
La “retta” r è il cerchio massimo che passa per i due poli P1 e P2. Preso un punto P sul “piano” ,ossia la superficie sferica, notiamo che qualsiasi “retta” s passante per P ( essendo per definizione un cerchio massimo) intersecherà sempre la “retta” r in due punti diametralmente opposti. In particolare potrebbe intersecarla nella coppia di punti P1 e P2. Affermare che tutte le possibili rette s intersecano r corrisponde a dire che tra esse non esiste alcuna parallela ad r.

La descrizione delle proprietà generali delle figure che si possono tracciare in questa geometria esula dallo scopo di questo articolo, il cui intento è solo di ricordare come le basi matematiche rivoluzionarie su cui è stata costruita la teoria della relatività, sono state gettate in pochi decenni da menti geniali, dopo secoli e secoli di confortevole tradizione. Non avrebbe potuto esserci, senza questo stravolgimento, l’altra rivoluzione che ha condotto con Einstein, alla fisica moderna.

Esiste anche una considerazione su cui vale la pena di riflettere. Non è così inconsueto nella nostra vita quotidiana maneggiare oggetti a geometria iperbolica ed ellittica. Tutte le volte che si toglie o si applica un copertone a una ruota si collegano o scollegano le due geometrie.

Il cerchione presenta una curvatura negativa, il copertone una curvatura positiva. Insieme compongono un toroide. Il sottile confine costituito dalle due circonferenze dei loro bordi è l’unica regione in cui la geometria è quella del piano euclideo. Eppure questa regione, così esigua, è proprio quella a cui siamo istintivamente sensibili, al punto di non riuscire a concepirne altre, se non con l’aiuto dell’acuto sguardo di grandi matematici.