Categorie: Matematica
Tags: allineamento circonferenza circoscritta geometria perpendicolari ai lati quiz triangolo qualsiasi
Scritto da: Vincenzo Zappalà
Commenti:4
(QI) Allineati e coperti! ***
Per un paio di giorni sarà difficile che possa usare il PC (solita iniezione all'occhio), lascio, perciò, un problemino molto carino ai "solutori più che abili". Divertitevi senza usare trigonometria e coordinate cartesiane.
Consideriamo un triangolo ABC qualsiasi e la sua circonferenza circoscritta. Da un qualsiasi punto P della circonferenza, non coincidente con uno dei vertici, tracciamo le perpendicolari ai tre lati (o ai loro prolungamenti). I tre punti di intersezione sono allineati. Dimostrarlo.
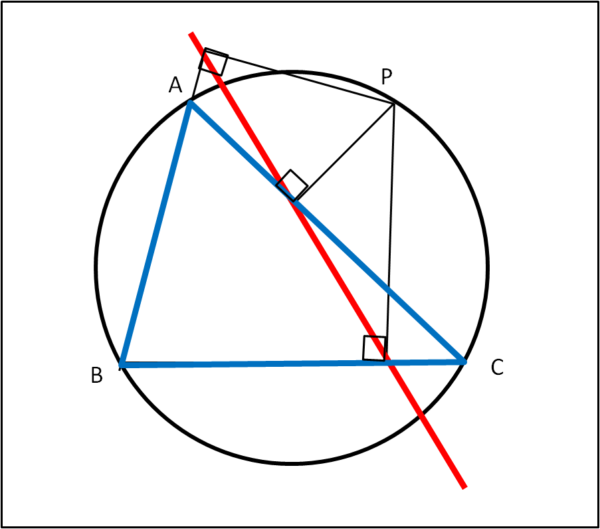
Questi triangoli... hanno solo tre lati, ma quante proprietà misteriose!






4 commenti
Provo a "tuffarmi"....
Un quadrilatero si definisce ciclico quando è perfettamente inscrivibile in una circonferenza.
Una sua peculiarità è che la gli angoli opposti sono supplementari, cioè la loro somma vale 180°.
Nella seguente figura, ho unito il vertice A (del triangolo qualsiasi ABC) con P e il vertice C dello stesso triangolo sempre con P; dalla stessa si evince che i quadrilateri ABCP, AXPZ, CPXY sono ciclici:
 Figura 1
Figura 1
ABCP perché perfettamente inscritto in una circonferenza;
AXPZ perché gli angoli opposti ∠AZP e ∠AXP sono retti per costruzione (∠AZP + ∠AXP = 90 + 90 = 180);
CPXY perché gli angoli ∠PXC e ∠PYC sono retti per costruzione e risiedono “sulla stessa parte” delle sue due diagonali CX e PY (per chiarire, un esempio in questa figura con gli angoli uguali che insistono sullo stesso arco rappresentati da pallini dello stesso colore):
Figura 2
In riferimento alla Figura 1,
per il quadrilatero ciclico ABCP: ∠APC + ∠B = 180 → ∠APC = 180 − ∠B
Per il quadrilatero ciclico BYPZ:
∠ZPY + ∠B = 180 → ∠ZPY = 180 − ∠B
per cui: ∠APC = ∠ZPY = 180 − ∠B
Operando una determinazione di angoli ottenuti per sottrazione, si può scrivere:
∠ZPA = ∠ZPC − ∠APC = ∠ZPC − (180 − ∠B) = ∠ZPC − 180 + ∠B
∠CPY = ∠ZPC − ∠ZPY = ∠ZPC − (180 − ∠B) = ∠ZPC − 180 + ∠B
quindi ∠ZPA = ∠CPY
Per il quadrilatero ciclico AXPZ: ∠ZPA = ∠ZXA perché insistono sullo stesso arco AZ della sua circonferenza;
per il quadrilatero ciclico CPXY: ∠CPY = ∠YXC perché insistono sullo stesso arco CY della sua circonferenza;
essendo uguali i primi membri delle due eguaglianze, saranno uguali anche i secondi membri,
quindi: ∠ZXA = ∠YXC
A questo punto la dimostrazione è fatta (se ∠ZXA = ∠YXC questi sono angoli opposti di due rette incidenti…) ma per essere ancora più chiari, ponendo gli angoli uguali tra loro ∠ZPA = ∠CPY = ∠ZXA = ∠YXC pari ad α, cioè: ∠ZPA = ∠CPY = ∠ZXA = ∠YXC = α , si avrà che:
∠PXZ = 90 − α; ∠PXY = 90 + α ; → ∠PXZ + ∠PXY = 90 − α + 90 + α = 180
ovvero l’angolo ∠YXZ è un angolo piatto e i punti X, Y, Z giacciono sulla stessa retta.
caro Andy,
ti dispiacerebbe essere un po' più chiaro a questo riguardo?
CPXY perché gli angoli ∠PXC e ∠PYC sono retti per costruzione e risiedono “sulla stessa parte” delle sue due diagonali CX e PY (per chiarire, un esempio in questa figura con gli angoli uguali che insistono sullo stesso arco rappresentati da pallini dello stesso colore).
Sarò più chiaro (e semplice):
il quadrilatero CPXY si può vedere come l'insieme di due triangoli rettangoli CXP e CYP che condividono la stessa ipotenusa PC: allora esisterà una circonferenza di diametro PC che contiene entrambi; congiungendo X con Y si ottiene il quadrilatero suddetto che essendo inscritto in una circonferenza (in verità, mezza ), sarà senz'altro ciclico.
), sarà senz'altro ciclico.
Perfetto Andy! Sei sempre una sicurezza...