Il quiz non era altro che la dimostrazione dell'esistenza della retta di Simson, formulata dal matematico scozzese Robert Simson (1687-1786), ma dimostrata solo nel 1796 da William Wallace.

La dimostrazione data da Andy è perfetta e io mi limito a proporre una dimostrazione del tutto simile, arricchita da qualche figura e passaggio in più...Il punto chiave della dimostrazione è la conoscenza delle caratteristiche dei quadrilateri  ciclici, ossia di quei quadrilateri che sono inscritti in una circonferenza. Per loro vale la proprietà che gli angoli opposti sono supplementari. Vale anche il contrario, ossia se in un quadrilatero gli angoli opposti sono supplementari il quadrilatero è ciclico, ossia è inscrivibile in un cerchio.

Consideriamo allora la nostra configurazione di partenza, ossia il triangolo ABC e  un punto P che stia sulla circonferenza inscritta al triangolo ABC (esiste sempre). Tracciamo poi le normali da P ai tre lati del triangolo individuando i punti H, K e L, come mostra la Fig. 1

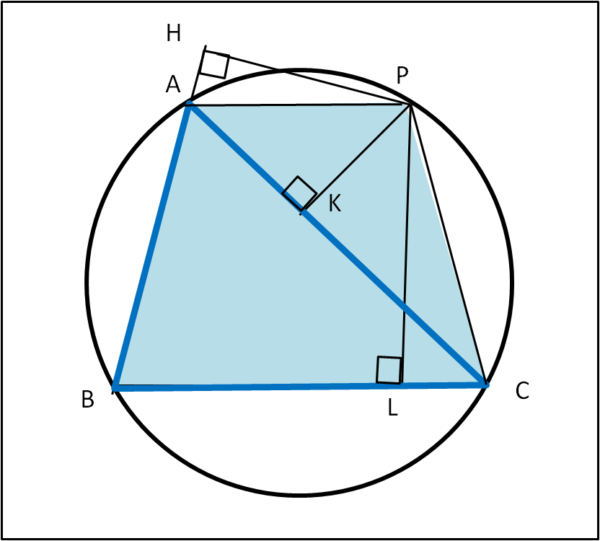
Il quadrilatero ABCP è ciclico per costruzione, per cui si può scrivere che:

ABC = 180 - APC                         .... (1)

Passiamo ora al quadrilatero HBLP (Fig. 2)

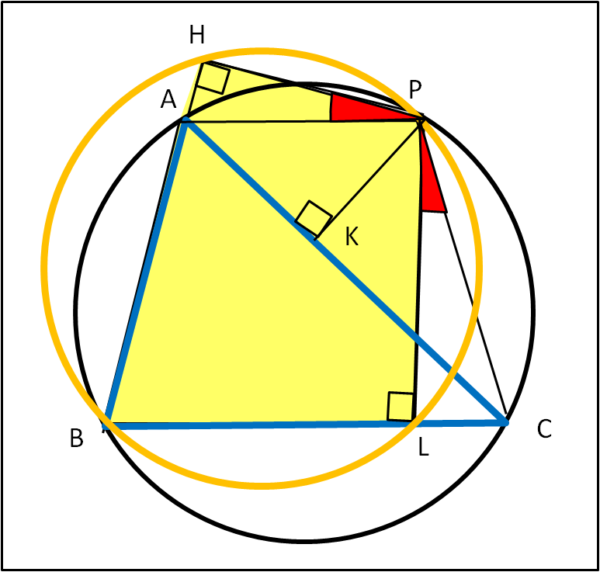
Anch'esso è ciclico in quanto gli angoli in H e in L sono retti per costruzione. Ne segue che la loro somma è 180° e, di conseguenza, il quadrilatero è ciclico. Possiamo, allora, scrivere che:

ABC = 180 – HPL

Ma, ricordando la (1) si ha che:

180 - APC = 180 - HPL

APC = HPL

HPL = HPA + APL

APC = LPC + APL

HPA + APL = LPC + APL

HPA = LPC                                   .... (2)

i due angoli rossi sono uguali

Consideriamo, adesso, il quadrilatero HPKA.

Gli angoli in H e K sono retti, per cui la loro somma è 180°. Ne segue che anche questo quadrilatero è ciclico ed esiste un suo cerchio circoscritto (Fig. 3)

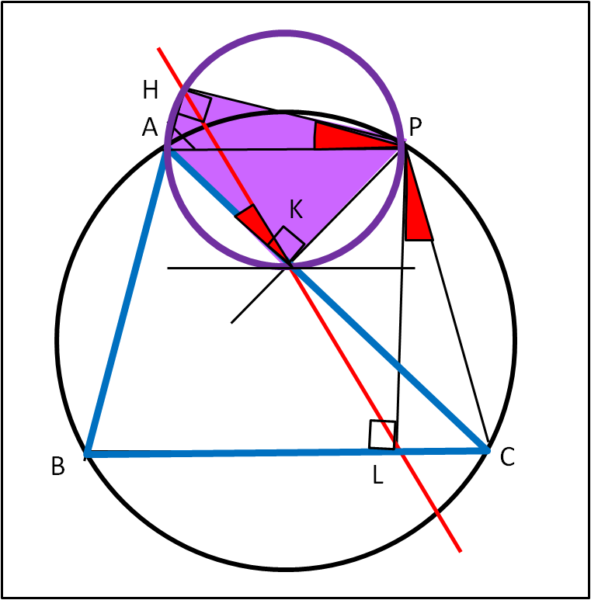
Notiamo che gli angoli HPA e HKA sono angoli alla circonferenza che insistono su uno stesso arco di cerchio (HA). Ne segue che devono essere uguali:

HPA = HKA

Ma, per la (2):

LPC = HKA                        .... (3)

Consideriamo, infine, il quadrilatero PKLC (Fig. 4)

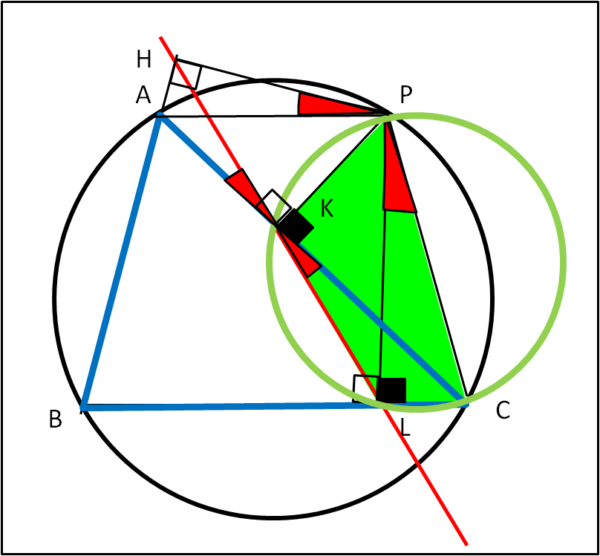
Gli angoli PKC e PLC sono entrambi retti. Il che vuol dire che deve esistere una circonferenza tale che PC ne sia il diametro. In altre parole anche PCLK deve essere ciclico. Possiamo allora scrivere che gli angoli alla circonferenza LPC e CKL sono uguali:

LPC = CKL

Ma, dalla (3) si ottiene

HKA = CKL                      .... (4)

HK sta dalla parte opposta di KL rispetto alla retta AKC. Ne segue che la (4) impone che HKA e CKL siano angoli alterni interni di due rette intersecantesi in K.  Una è  AKC e l'altra è proprio HKL. I tre punti H, K e L sono, perciò, allineati!

c.v.d.